§ 6. Использование элементов теории вероятности и математической статистики для определения оптимальных трансформаций аномального поля

Основной проблемой трансформации гравитационных аномалий является определение оптимальных параметров трансформация при которых обеспечивается наиболее полное выделение аномалий объектов, представляющих интерес при решении данной геологи­ческой задачи. Выбор оптимальных параметров опирается на ком­плекс сведений об аномальных объектах: форма, размеры, глубина залегания и т. п. Количественная и качественная информация может быть получена из общегеологических соображений, данных других методов, анализа самого гравитационного поля. Естественно, чем больше имеется сведений об аномальных массах, тем более обосно­ванно можно выбрать оптимальные параметры трансформации.

Однако большинство существующих методов трансформаций не учитывает всего многообразия явлений, определяющих результаты трансформации, а также не учитывает случайного характера этих явлений. Поэтому выбор оптимальной трансформации должен основываться на знании статистических закономерностей явлении, отра­женных в суммарном гравитационном поле. При таком подходе можно использовать статистические характеристики отдельных соста­вляющих суммарного гравитационного поля, т. е. наиболее общие сведения об исследуемых объектах. Следует учитывать, что как сами предпосылки, так и полученные на их основе выводы относятся не к отдельным аномалиям и аномальным телам, а к статистическим совокупностям аномалий и аномальных тел. Поэтому для решения задачи привлекается аппарат математической статистики, в частности теория случайных функций.

Использование аппарата теории случайных функций для выбора оптимальных трансформаций рассматривается в работах И. Г. Клушина, К. В. Гладкого, М. Г. Сербуленко, О. А. Соловьева и др.

Случайной называется функция, которая в результате опыта может принять тот или иной конкретный вид, заранее неизвестный. Этот конкретный вид называется реализацией случайной функции. Проведя над случайной функцией серию опытов, получим группу, или семейство, реализаций этой функции. Приведем пример. Поле силы притяжения U_z какого-либо тела можно рассматривать как случайную функцию координат точки наблюдения. Если измерить поле вдоль профиля несколько раз, то каждая кривая U_z(x) будет представлять собой реализацию случайной функции, и совокупность этих кривых образует семейство реализаций (см. рисунок). Каждая реализация есть обычная, неслучайная, функция; 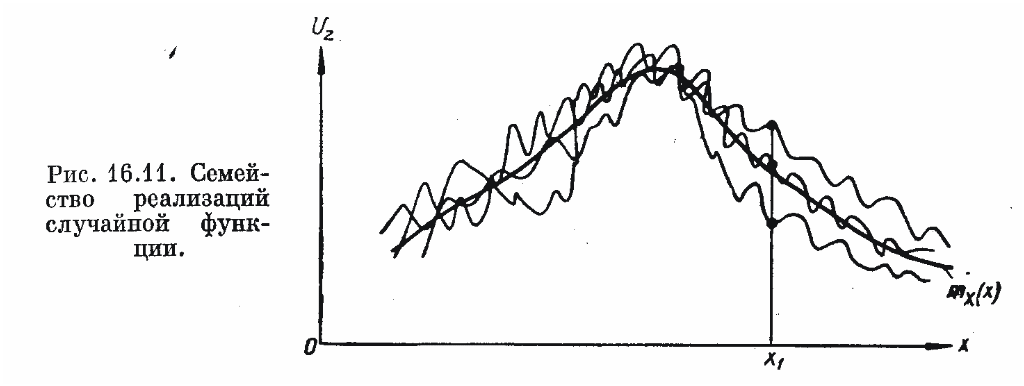таким образом, в результате каждого опыта случайная функция превращаете в не случайную. Если зафиксировать значение аргумента х = х₁ то случайная функция превратится в случайную величину. Эта случайная величина называется сечением случайной функции U_z npи данном х. Если сделать сечение семейства реализаций, то найдем значений случайной величины U_z, полученной в n опытах.

Для характеристики случайных величин пользуются числовыми характеристиками этих величин: математическим ожиданием М и дисперсией D. Математическое ожидание М случайной величины определяется равенством

M(X) = = , (119)

где p_i - вероятности возможных значений x_i случайной величины X,

= 1.

Математическое ожидание случайной величины иногда называю средним значением этой величины.

Формула (119) относится к прерывной случайной величине. Для непрерывной величины X математическое ожидание определяется интегралом

M(X) = , (120)

где f(х) - плотность распределения величины X,

= 1.

Дисперсия D случайной величины X для дискретного и непрерывного ее распределения выражается соответственно формулами

D(X) = ,

D(X) = . (121)

Дисперсия случайной величины характеризует рассеивание, разброс, ее значений около математического ожидания.

Средним квадратическим отклонением (стандартом) называют

σ(X) = .

Аналогичными характеристиками описывают и случайные функ­ции. Характеристики случайных величин представляют собой числа, а характеристиками случайных функций в общем случае являются не числа, а функции.

Математическим ожиданием случайной функции X(х) называется неслучайная функция m_X(x), которая при каждом значении аргумента х равна математическому ожиданию

соответствующего сечения случайной функции:

m_X(x) = M(X(x)).

М атематическое ожидание случайной функции есть некоторая средняя функция, около которой различным образом варьируют конкретные реализации случайной функции (см. рисунок).

Дисперсией случайной функ­ции X(х) называется неслу­чайная функция D_X(x), значе­ние которой для каждого аргу­мента х равно дисперсии соот­ветствующего сечения случай­ной функции:

D_X(x) = D(X(x)).

Дисперсия случайной функции характеризует разброс возможных реализаций функции относительно ее математического ожидания, т. е. степень случайности случайной функции.

Средним квадратическим отклонением случайной функции назы­вают функцию

σ_X(x) = .

М атематическое ожидание и дисперсия являются важными харак­теристиками случайной функции, но для описания особенностей случайных функций этих характеристик недостаточно. При одинако­вом математическом ожидании и одинаковой дисперсии (см. рисунок) две случайные функции Х₁(x) и Х₂(х) имеют совершенно различный вид, определяемый их конкретными реализациями: для функции Х₁(х) характерно плавное изменение, для функции Х₂(х) - не­правильные колебания. Различие в плавности изменения функций Х₁(х) и Х₂(х) ни дисперсия, ни математическое ожидание описать не могут. Для этого вводится специальная характеристика, называемая корреляционной (автокорреляционной) функцией. Корреляционная функция характеризует степень зависимости между сечениями случайной функции, относящимися к различным аргу­ментам х. Рассмотрим два сечения функции X(х), относящиеся к х₁ и х₂ (см. рисунок). Очевидно, чем ближе значения х₁ и х₂, тем б лиже и значения функции X(x₁) и X(x₂). Очевидно также, что с увеличением интервала τ между сечениями связь X(х₁) и X(х₂) вообще должна убывать.

Функция автокорреляции определяется выражением

K_X(x₁, x₂) = M((X(x₁) – m_X(x₁))(X(x₂) – m_X(x₂))). (122)

Полагая х₁ = х₂, имеем

K_X(x, x) = M((X(x) – m_X(x))²) = D_X(x). (122)

т. е. при х₁ = x₂ корреляционная функция обращается в дисперсию случайной функции.

Вместо корреляционной функции К_X(х₁, х₂) часто используют нормированную корреляционную функцию

R_X(x₁, x₂) = , (123)

которая представляет собой коэффициент корреляции величин X(x₁) и X(х₂) при х₁ = х₂ = х

R_X(x, x) = = = 1.

Случайная функция называется стационарной, если ее математическое ожидание и дисперсия постоянны, а корреляционная функ­ция зависит только от разности аргументов х₁ - х₂ = τ

m_X(x) = const, D_X(x0 = const,

K_X(x₁, x₂) = K_X(x₂ – x₁) = K_X(τ).

Нормированная корреляционная функция стационарной случай­ной функции (коэффициент корреляции) определяется выражением

R_X(τ) = = .

Коэффициент корреляции изменяется от нуля до единицы: R_X(τ) = 0 показывает, что никакой корреляции между X(х) и X(х + τ) нет, R_x (т) = 1 соответствует полной корреляции (см. рисунок). У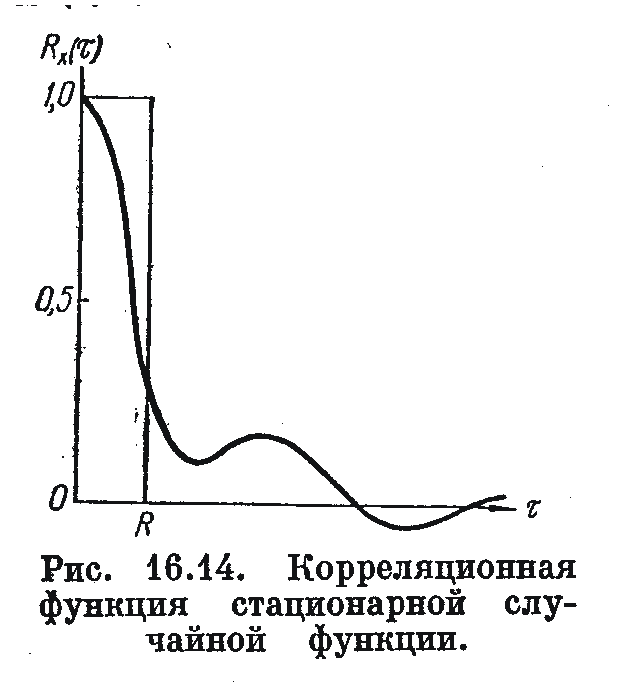 читывая, что при больших τ корреляционная функция обращается в нуль, в большинстве практических случаев считают, что корреляция исчезает при R_X(τ) = 0,3. Величину τ, при которой R_X(τ) = 0,3, называют радиусом автокорреляции R. Иногда за радиус корреляции принимают площадь, ограниченную кривой R_X(τ) и осью х:

R = .

Форма кривой R_X(τ) и радиус автокорреляции R позволяют судить о степени изменчивости функции X(х) при изменении х. При слабой коррелируемости кривая R_X(τ) убывает быстро, при плавной функции X(х) кривая R_X(τ) изменяется медленно. При наличии периодичности в функции X(х) кривая R_X(τ) становится знакопеременной. Для большинства практических слу­чаев коэффициент корреляции может быть аппроксимирован выражениями

R_X(τ) = ,

R_X(τ) = , (124)

где N - некоторое постоянное число.

Гравитационные аномалии можно рассматривать как стационарные слу­чайные функции, поскольку их кон­кретные реализации непрерывно коле­блются около средней функции, амплитуда и резкость этих коле­баний постоянны на протяжении всего отрезка задания аномалии. Стационарная случайная функция называется эргодической, если одна-единственная конкретная реализация достаточной продолжи­тельности дает хорошее представление о свойствах случайной функ­ции в целом. Эргодическое свойство состоит в том, что каждая отдель­ная реализация случайной функции является представительной Для всей совокупности реализаций и может заменить эту совокуп­ность. Стремление корреляционной функции К_X(τ) к нулю при τ → ∞ указывает на эргодичность функции. Для эргодических стационарных функций существенно упрощается опре­деление их характеристик, в частности, математическое ожидание и автокорреляционную функцию можно приближенно найти по одной представительной реализации:

M(X(x)) = m_X = , (125)

K_X(τ) = . (126)

Разбивая интервал интегрирования L на n равных частей длиной ∆х = L/n, для математического ожидания вместо формулы (125) имеем

m_X = . (127)

Аналогично можно вычислить корреляционную функцию для значений τ = q∆x:

K_X(τ = q∆x) = , (128)

где

X^/_I = X_i – m_X.

При q = 0

D_X = K_X(0) = . (129)

Вычисление корреляционной функции проводят для q = 0, 1, 2 … до таких значений q, при которых корреляционная функция стано­вится практически равной нулю или начинает совершать колебания около нуля. Для определения m_X и K_X с удовлетворительной точ­ностью надо, чтобы число точек n было достаточно большим (100 или более).

При исследовании случайных функций широко используют ее спектральное представление. Различие спектрального представления случайной стационарной и неслучайной функции состоит в том, что для случайной функции амплитуды колебаний являются случайными величинами. Спектром случайной стационарной функции описы­вается распределение дисперсий по различным частотам

D_X = , (130)

функция G(ω) называется спектральной плотностью стационарной случайной функции.

Формула (130) представляет собой разложение дисперсии D_X на сумму элементарных слагаемых G(ω)dω, каждое из которых является дисперсией, относящейся к элементарному участку частот dω. Функцию G(ω) называют еще энергетическим спектром случайной функции. Энергетический спектр описывает частотный состав стационарного процесса. Эта характеристика случайной функции не является самостоятельной, а полностью определяется корреляционной функцией. Согласно теореме Винера - Хинчина

корреляционная функция и спектральная плотность связаны следующими соотношениями :

K_X(τ) = ,

G(ω) = . (131)

Так как K_X(τ) и G(ω) являются четными функциями своих аргументов, то это соотношение можно записать в виде

K_X(τ) = ,

G(ω) = . (132)

Для изотропной (обладающей круговой симметрией) стационарной случайной функции, зависящей от двух координат, формулы (130) и (132) принимают вид

D_X = K_X(0) = = 2π ,

K_X(τ) = 2π , (133)

(ω) = .

Формулы (131) - (133) имеют большое значение и широко используются при исследовании линейных преобразований, совершаемых над случайными стационарными функциями. Линейными называются такие преобразования, при которых оператор преобра­зования обладает свойством аддитивности. Примерами линейного преобразования являются операторы дифференцирования, умноже­ния на определенную функцию, интегрирования с заданным «весом» и т. д. Все используемые трансформации и преобразования гравита­ционных аномалий являются линейными операторами.

При линейном преобразовании стационарной случайной функции ее спектральная плотность умножается на квадрат модуля частотной характеристики преобразования:

G_tr(ω) = G(ω)|Ф(ω)|², (134)

где G_tr(ω) - спектральная плотность трансформированной функции.

Применим полученные формулы для построения оптимальной трансформации, в результате которой из суммы двух стационарных случайных функций должна быть выделена одна из них. Задача построения оптимальной трансформации для этого случая рассмотрена И. Г. Клушиным. Пусть суммарной случайной функцией является наблюденная вдоль профиля гравитационная аномалия U, состоящая из аномалии U_r, которая подлежит выделению, и ослож­няющей ее аномалии U_n:

U = U_r + U_n.

Конкретно функция U_n может проявляться в виде региональной или локальной аномалии более высокого порядка, чем U_r в виде погрешности наблюдений и т. д.

В качестве критерия оптимальности трансформации возьмем минимум средней квадратической погрешности приближения транс­формированной аномалии U_tr к значениям аномалии U_r, которые наблюдались бы при отсутствии помехи U_n. При этом предпола­гается, что аномалии U_r и U_n не коррелируются друг с другом (коэф­фициент взаимной корреляции равен нулю):

K_{r, n}(τ) = K_{n, r}(τ) = 0.

Если G_r(ω) и G_n(ω) - спектральные плотности аномалий U_r и U_n, то после преобразования спектральные плотности этих аномалий будут

G_r^(tr) = G_r(ω)|1 - Ф(ω)|², G_n^(tr) = G_n(ω)|Ф(ω)|²,

Величина G_r(со) | 1—Ф (со)|² определяет искажения, вносимые трансформацией в выделяемую аномалию U_r. Среднее значение квадрата суммарной ошибки, возникающей в результате трансформации, получаем из выражения

. (135)

Характеристику преобразования Ф(ω) необходимо подобрать таким образом, чтобы интеграл (135) имел наименьшее значение. По­скольку в него входят только спектральные плотности аномалии и помехи, учитывающие амплитуды составляющих, а не их фазы, то характеристика трансформации является вещественной функцией. Минимальное значение интеграл принимает при

Ф(ω) = . (136)

Имея в виду равенство (93), получаем выражение для функ­ции U, подвергнутой трансформации,

U_tr(x, 0) = . (137)

Если функция Ф(ω) такова, что интеграл равномерно сходится, то, поменяв порядок интегрирования в правой части выражения (137), получим

U_tr(x, 0) = , (138)

где

K(ξ – x) = = 2 (130)

K(ξ – x) - весовая функция оптимальной трансформации.

На основе формулы (138) можно построить палетку. Пусть точки наблюдений расположены через равные интервалы ∆х, так что х = n∆х. Тогда выражение (138) преобразуется в сумму

U_tr(n) = (U(n)K(0) + , (140)

где

K(m) = 2 .

Значениями K(m) определяются числовые коэффициенты палетки. На основе формулы (140) можно рассчитать палетку и с рав­ными весовыми коэффициентами.

Таким образом, для построения оптимальной трансформации необходимо знать спектральную плотность G(ω) разделяемых аномалий, которую определяют по функции автокорреляции К_х(τ). При вычислении G(ω) по графику К_х(τ) используют различные приемы численного интегрирования или аппроксимируют К_х(τ) формулой

К_х(τ) = , (141)

Тогда

G(ω) = . (142)

Для приближенной оценки G(ω) и К_х(τ) можно пользоваться средним значением квадрата амплитуды выделяемых аномалий и ра­диусом их корреляции R. На основе формулы (140) можно построить оптимальные трансформации для различных конкретных случаев распределения аномалий. Аналогичным приемом можно получить формулы оптимальной трансформации и для трехмер­ной задачи.

В случае, когда полезные аномалии соизмеримы с уровнем слу­чайных помех, задача выделения аномалий может быть решена на основе корреляции ожидаемого и наблюденного распределения аномалий. Н. Винером было показано, что оптимальным оператором для выделения слабых сигналов на фоне сильных помех является такой оператор, который осуществляет взаимную корреляцию вход­ной функции и полезного сигнала. В этом случае участки записи, частотная характеристика которой совпадает с частотной характе­ристикой ожидаемого сигнала, выделяются наиболее рельефно, т. е. оптимально выявляется полезный сигнал. Задача разделения аномалий может быть сформулирована следующим образом.

Имеется дискретное распределение значений аномалии U (х), известно также, что в некоторых точках этого распределения присутствует искомая аномалия U_r(x), которая осложнена поме­хами U_n(х). Требуется оценить наблюденные значения с точки зрения наличия или отсутствия аномалии U_r(x). Эта задача получила исчерпывающее решение в теории информации. В практическом приложении она нашла широкое применение в радиолокации. Применение этого метода выделения слабых геофизических аномалий рассмотрено в работах А. Г. Тархова, А. А. Сидорова, В. Н. Ники­тина, О. А. Демидовича и др. Решение задачи в такой постановке сводится к статистической оценке наблюденного поля в отношении отсутствия или наличия U_r(x). Решению придается вероятностный смысл с указанием надежности. Задача может быть решена на основе теоремы гипотез Байеса, которая позволяет определить вероятность причин, если заданы вероятности следствий.

Относительно полезной аномалии U_r(x) имеются две гипотезы: гипотеза Н_г - аномалия U_r(х) есть, и гипотеза Н_о - аномалии U_r(х) нет. Вероятности реализации каждой из гипотез неизвестны. Можно предполагать, что обе гипотезы равновероятны. Это предположение отвечает максимальной неопределенности, т. е.

P(H_r) = P(H₀) = 0.5.

Если известны условные вероятности (функции правдоподобия) наблюденной аномалии: Р[U (x₁)/H_r] при наличии полезной ано­малии и Р(U(x_i)/H₀] при отсутствии ее, то формула Байеса позво­ляет до распределению U(x_t) (i = 1, 2, . . ., n) вычислить условную вероятность наличия полезной аномалии

P(H_r/U(x_i)) = = (143)

и условную вероятность отсутствия полезной аномалии P(H₀/U(x_i)) = = , (144)

где = L (145)

- отношение правдоподобия.

Очевидно, аномалия будет выделена, если L ≥ 1. Таким образом, для суждения о наличии полезной аномалии U_r необходимо вычис­лить отношение правдоподобия L, т. е. определить численные зна­чения условных вероятностей Р[U(x_t)/H_r] и Р[U(Х_i)/Н₀]. Найти их сравнительно просто, если наблюденные значения U(x_i) предста­вляются стационарной случайной функцией, а помехи не коррелированны, имеют нулевое среднее и распределены по нормальному закону Гаусса. Ожидаемые аномалии U_r(x_i) должны быть заданы. В этом случае условная вероятность Р[U(x_i/H₀] полностью определяется численными значениями U(x_iи распределением вероятностей нор­мального закона:

Р[U(x_i/H₀] = exp(- ), (146)

где i = 1 2, . . ., m - порядковый номер точки наблюдения; q - порядковый номер аномального значения на интервале n.

Если из наблюденного значения U(х_i) вычесть поточечно значе­ния U_r(х_q), то условная вероятность Р[U(x_i)/H_r] будет определена разностями U(x_i) - U_r(x_q) и нормальным законом распределения вероятностей:

P(U(x_i)/H_r) = exp(- ), (147)

(i = 1, 2, …, m).

Используя выражения (146) и (147), составляем отношение правдоподобия L (145) и, подставляя его в формулу (143). получаем выражение для определения искомой вероятности

P(H_r/U(x_i)) = . (148)

На основе этой формулы проводят практические вычисления по выделению аномалий, соизмеримых с помехами. Вероятности, превышающие 0,5, определяют местоположение искомых аномалий.

Следует отметить, что рассмотренный метод выделения аномалий дает положительные результаты, если соблюдаются условия, при которых получена формула (148), т. е. помехи не коррелированны и распределены по нормальному закону, а полезная аномалия должна быть полностью определена. Поэтому перед вычислениями наблю­денную кривую необходимо любым подходящим способом преобра­зовать в знакопеременную, привести ее к нулевому среднему и вычислить дисперсию. Ожидаемая аномалия выбирается таким образом, чтобы она оптимально соответствовала полезной аномалии и была подобна ей по форме. Дисперсия ожидаемой аномалии должна быть равна дисперсии помех, сумма ординат аномалии должна быть равна нулю. Эти требования к ожидаемой аномалии определяют оптималь­ные условия выделения полезных аномалий.