§ 8. Решение прямой и обратной задач для вертикальной материальной полосы и вертикального тонкого пласта.

Геологическим аналогом вер­тикальной материальной полосы могут служить различные круто­падающие линзообразные и жилообразные тела при условии, что их горизонтальная мощность зна­чительно меньше вертикальной и глубины залегания.

Для вычисления элементов гравитационного поля вертикальной полосы надо в общих интегральных выражениях для производных потенциала притяжения

U_x(x, z) = 2kσ , U_z(x, z) = 2kσ ,

U_y(x, z) = 0, U_xz(x, z) = 4kσ ,

U_zz(x, z) = U_∆(x, z) = 2kσ ,

U_yz = U_xy = 0, где r =

положить σdξ = μξ (μ - поверхностная плотность полосы) и интегрирова­ние проводить только по перемен­ной ζ в пределах от h₁ до h₂ (h₁ и h₂ - глубина верхнего и ниж­него конца полосы). Полагая, что начало координат находится над вертикальной полосой, имеем

U_z(x, 0) = ∆g(х, 0) = 2kμ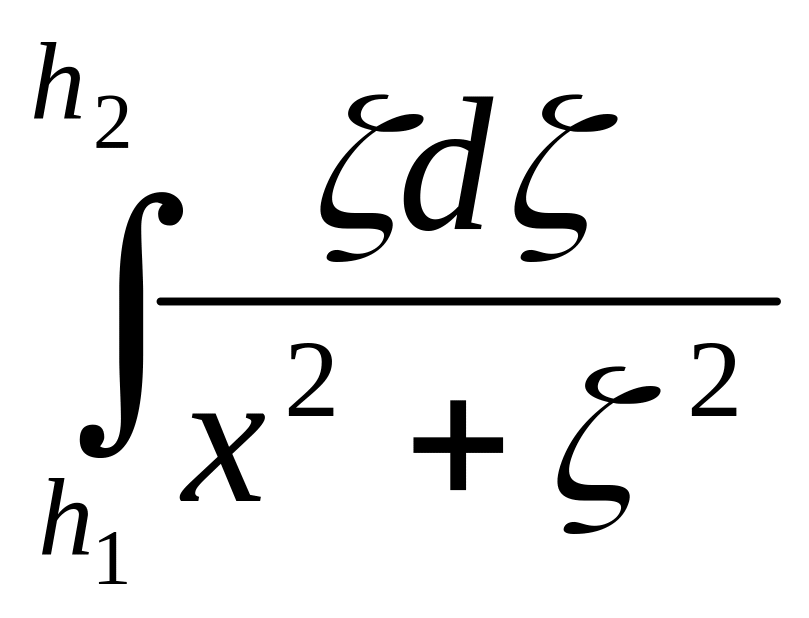 = kμln ,

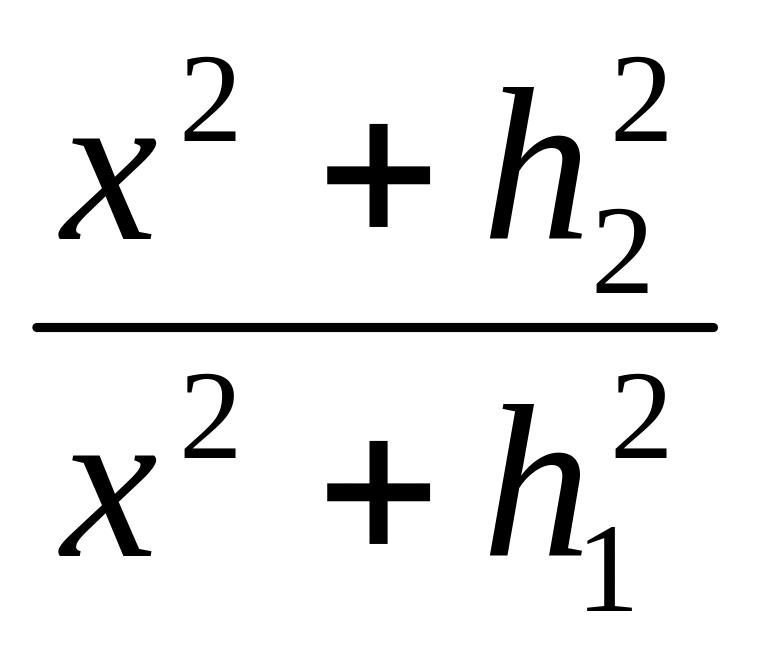U_xz(x, 0) = -4kμ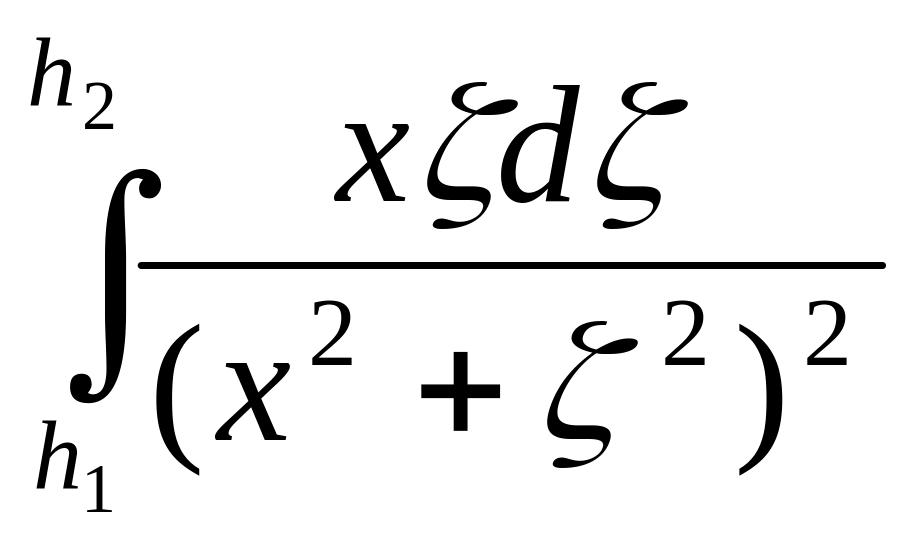 = 2kμ( - ),

U_zz(x, 0) = 2kμ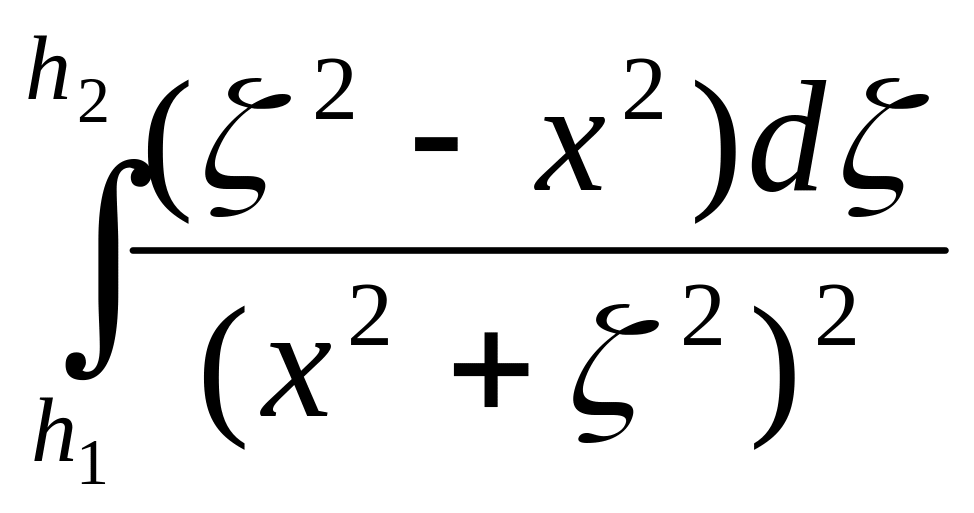 = 2kμ( - ).

При h₂ → ∞, т. е. когда вертикальная полоса имеет бесконечное простирание на глубину, обозначив h₁ = h, получим

U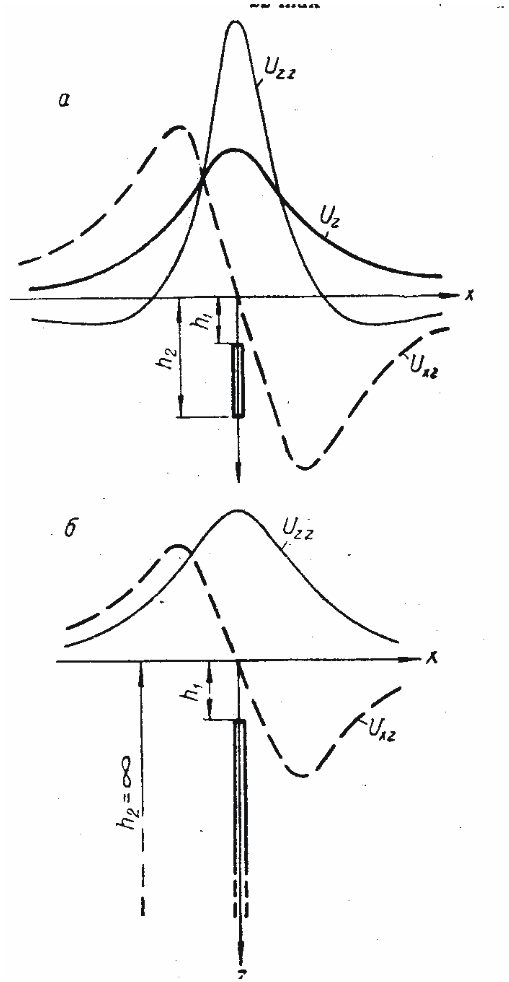 _xz(x, 0) = -2kμ ,

U_zz(x, 0) = 2kμ .

Функция U_z при h₂ → ∞ тоже стремится к бесконечности, что указывает на сильную зависимость ее от величины h₂.

Обратимся к формуле для аномалии силы тяжести:

U_z(x, 0) = ∆g(х, 0) = kμln ,

Функция U_z(x, 0) всюду положительна и достигает максимума в точке х = 0.

U_{z max} = 2kμln .

Кривая U_z убывает с увеличением |х| и при х = ± ∞ обращается в нуль. Для определения h₁ и h₂ найдем абсциссы x_1/2 и x_1/4, где U_z соответственно составляет U_{z mах}/2 и U_{z max}/4. Для указанных точек можно написать

kμln = kμln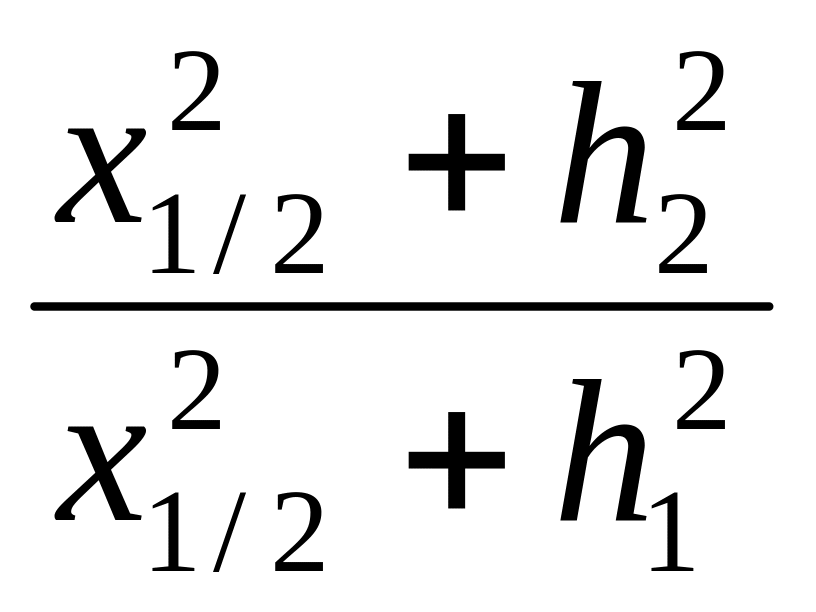 или = ,

kμln = kμln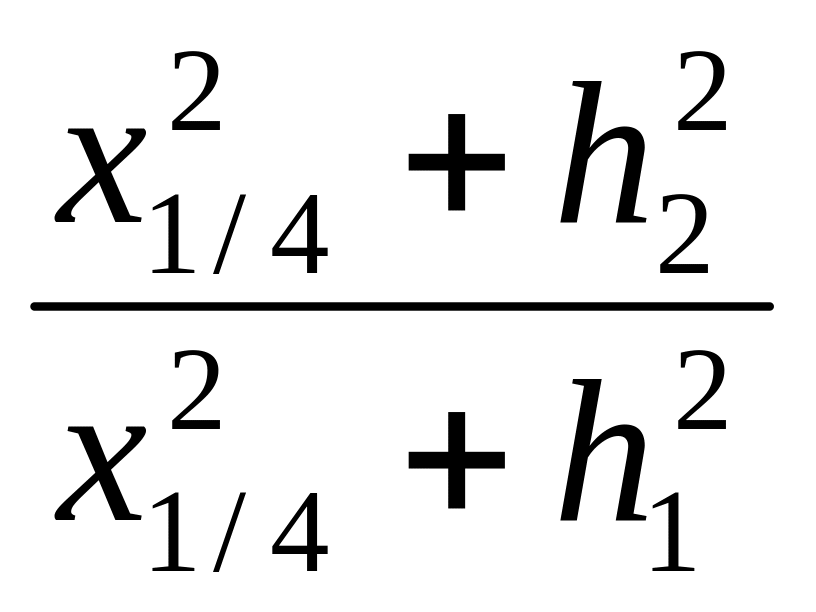 или = ( )².

Из этих равенств получаем

h₁h₂ = x_1/2²,

x_1/4² = h₁h₂ + (h₁ + h₂) .

Вводя обозначение

h₁ + h₂ = = 2m

используя свойства корней квадратного уравнения, находим

h₁ = m - ,

h₂ = m + ,

Определив h₁ и h₂ вычислим

μ = .

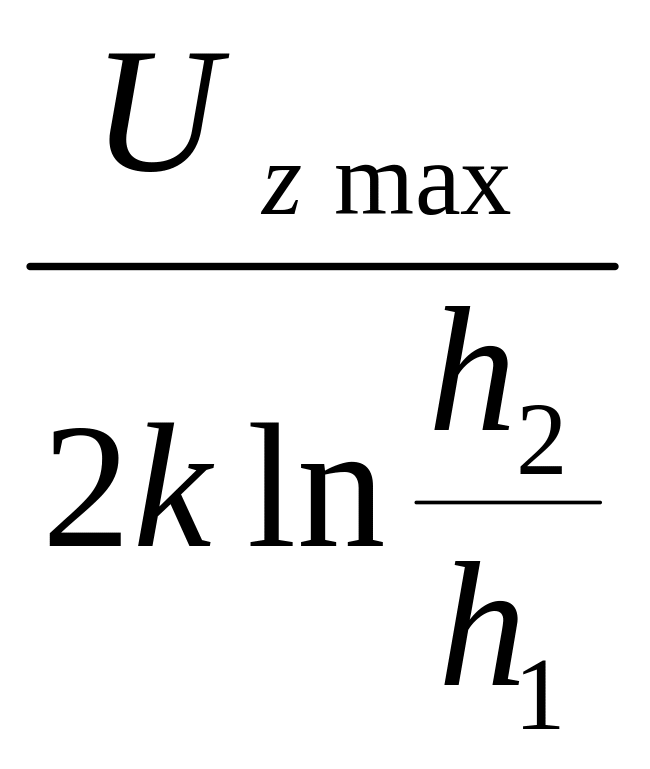Рассмотрим горизонтальную составляющую U_xz(х, 0), эта кривая положительна при х < 0, отрицательна при x > 0 и имеет экстре­мальные значения при

x_{max, min} = .

Найти аналитически по кривой U_хz параметры вертикальной полосы, ограниченной по падению на глубину, очень сложно. Задача ре­шается проще, если положить, что вертикальная полоса бесконечна на глубину. Тогда

U_xz(x, 0) = -2kμ .

Кривая U_хz(x, 0) в этом случае также положительна при х < 0 и отрицательна при х > 0, при x = 0 и x = ±∞ функция U_xz = 0. Исследование U_xz на экстремум дает

x_{max, min} = ±h, U_{z max} = .

По этим формулам находят h и μ.

Кривая вертикальной составляющей градиента силы тяжести

U_zz(x, 0) = 2kμ( - ).

положительна при |x| < |x_о| = b отрицательна при |x| > . При x = ±х₀ и x = ±∞ функция U_zz = 0. Максималь­ное значение функция U_zz имеет при х_mах = 0, минимальные при x_min = ^

U_{zz max} = 2kμ( - ), U_{zz min} = -2kμ .

Параметры вертикальной полосы по кривой U_zz находят по фор­мулам, которые аналогичны формулам кривой U_z. Имея в виду, что х₀² = h₁h₂, обозначаем

2m = .

Тогда

h₁ = m - , h₂ = m + ,

μ = .

Формула U_zz(x, 0) для вертикальной полосы, бесконечной на глубину, аналогична формуле U_z для горизонтального ци­линдра. Следовательно, для вычисления U_zz вертикальной полосы и определения ее параметров можно использовать выведенные ранее соотношения U_{z max} = и x_nh = для горизонтального цилиндра.