§ 6. Решение прямой и обратной задач для вертикального материального стержня и вертикального кругового цилиндра.

Геологические объекты, вертикальные размеры которых значи­тельно больше горизонтальных размеров, а последние малы но сравнению с глубиной залегания, могут быть уподоблены вертикальному круго­вому цилиндру или эквивалентному ему вертикальному материаль­ному стержню, расположенному на оси цилиндра и имеющему такое же распределение массы на единицу длины, как и цилиндр. При­мером таких геологических тел могут быть столбообразные рудные и интрузивные тела, соляные купола, кимберлитовые трубки и т. д.

Для вывода аналитических выражений гравитационного эффекта материального стержня поместим начало координат в точку проек­ции стержня на плоскость Оху, примем глубину верхнего конца стержня h₁ нижнего h₂, массу единицы длины стержня dm = λdζ, где λ - линейная плотность единицы длины стержня. Рассмотрим поведение элементов гравитационного поля вдоль профиля, про­ходящего над центром стержня (ξ = η = у = z = 0). При этих условиях воспользуемся выражениями:

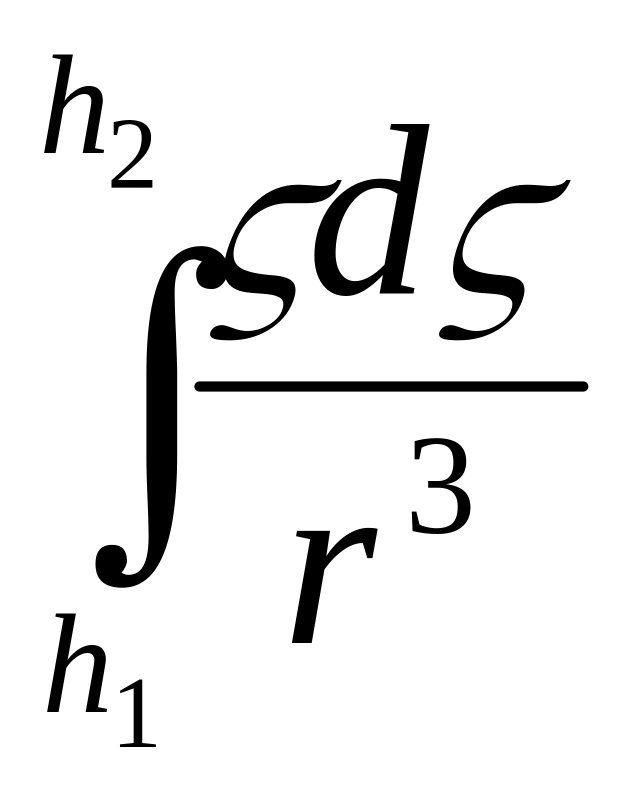U_z(x, 0, 0) = ∆g(x, 0, 0) = kλ = kλ( - ),

U_xz(x, 0, 0) = -3kλ = kλ( - ),

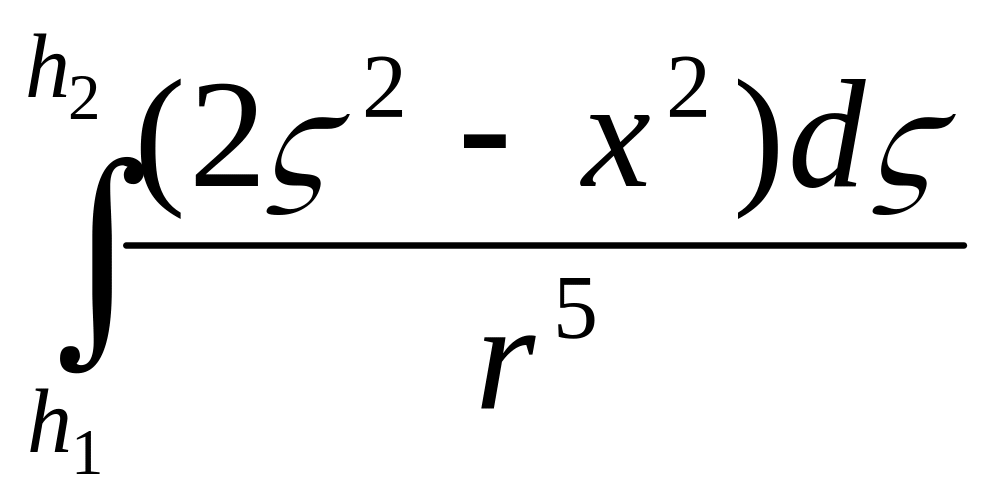U_zz(x, 0, 0) = kλ = kλ( - ),

где r = .

При h₂ = ∞, т. е. когда глубина нижнего конца стержня значи­тельно больше глубины верхнего, получим (приняв h₁ = h).

U_z(x, 0, 0) = ∆g(x, 0, 0) = ,

U_xz(x, 0, 0) = -3kλ = kλ( - ),

U_zz(x, 0, 0) = kλ = kλ( - ),

Обратная задача для материального вертикального стержня по U_zz(х, 0, 0) решается так же просто, как и для точечной массы. Исследование кривой U_z показывает, что она всюду положительна и имеет максимум при х = 0, который определяется по формуле:

U_{z max} =

Обозначив х_n абсциссу, где значение U_zn составляет n-ю долю от максимального (U_zn/U_{z max} = n), найдем значение n в виде:

n = .

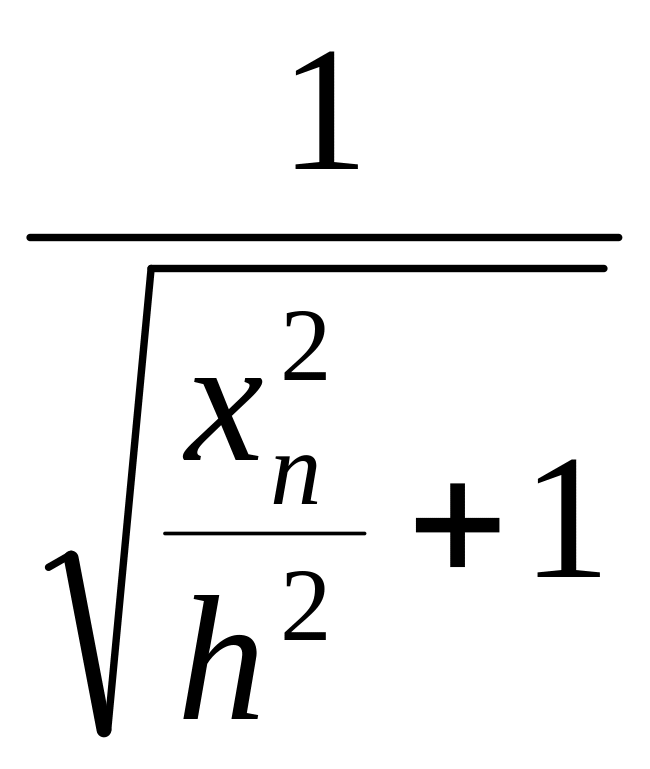Введя обозначение x_n/h = x_nh и решив последнее уравнение отно­сительно x_nh, получим:

x_nh = .

При n = ½ получим формулу для определения значения h:

h = x_1/2 .

Кривая U_xz(х, О, 0) положительна при х < 0 и отрицательна при х > 0; при x = 0 и x = ±∞ функция U_xz(х, 0, 0) = 0. Иссле­дование кривой на экстремум дает следующие значения:

x_max = - , x_min = + , U_{xz max} = 0.38 .

Обозначив x_min - x_max = L, получим L = h , что позволяет вычислить h.

Если значения U_xz известны по линии, не проходящей над центром стержня, то они могут быть приведены к центральному про­филю с помощью преобразования, рассмотренного выше для сферы.

Сравнение выражений U_zz(x, 0, 0) для вертикального бесконечного материального стержня и U_z(x, 0, 0) для материальной точки показывает, что эти выражения совпадают. Следовательно, глу­бину h стержня можно определять по той же формуле, что и материальной точки.