§ 15. Решение прямой и обратной задач для вертикального пласта

В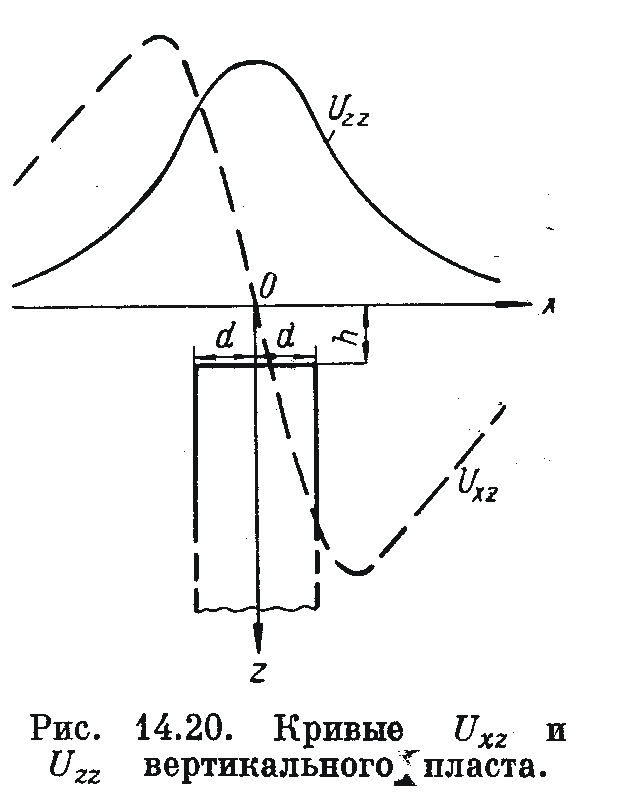 ертикальным пластом называется тело, ограниченное двумя параллельными вертикальными полуплоскостями и одной горизонтальной плоскостью. Очевидно, вертикальный пласт представляет собой частный случай наклонного слоя, для которого α = π/2 и Ф = π/2. Чтобы получить формулы U_xz и U_zz вертикаль­ного пласта (формулы U_z не рассматриваем, так как U_z = ∞) положим, что горизонтальная мощность пласта равна 2d, глубина залегания верхней кромки h. Начало координат поместим над сере­диной верхней кромки пласта, ξ₂ = -d, ξ₁ = dζ₂ = dζ₁ = h. Из выражения (4, § 14) следует:

U_xz(x, 0) = kσln = 2kσln , (1)

U_zz(x, 0) = 2kσ(arctg - arctg ) = 2kσΘ.

Рассмотрим кривую U_zz. Сравнивая формулы (1) для U_zz и формулы для U_z материальной горизонтальной по­лосы, видим, что они идентичны, если положить μ = σ. Таким образом, пове­дение U_zz вертикального пласта ана­логично поведению U_z материальной полосы. Следовательно, находить эле­менты вертикального пласта по кри­вой U_zz можно с помощью приемов, рассмотренных выше для материальной полосы.

Обратимся к анализу кривой U_хz.

Из формулы (1) следует, что при х = 0 и при х = ±∞ функция U_хz = 0, при х < 0 U_xz > 0, при х > 0 U_хz < 0, причем U_xz(-х) = -U_xz(+x).

Из условия dU_xz/dx = 0 имеем

x_{max, min} = , (2)

U_{xz max} = kσln = kσln

Пусть x_1/2 - абсцисса, где U_xz1/2 = U_{xz max}/2, тогда

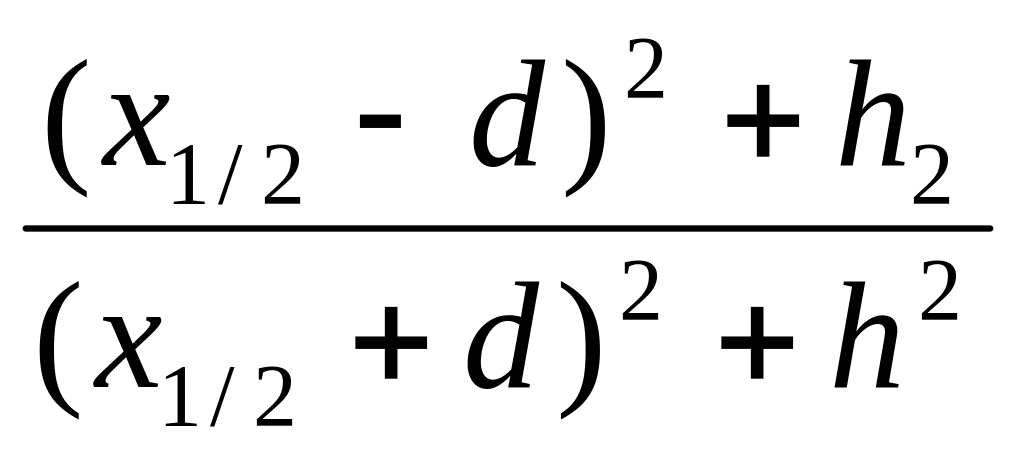( )² = .

Решая это уравнение совместно с выражением (2), получаем

d = , (4)

где a = . (3)

Следует отметить, что существуют две абсциссы x_1/2, одна из них по абсолютному значению меньше, а другая больше |x_max |. В фор­муле (3) используется |x_1/2 | < |x_max|. Из формулы (2) опре­деляем глубину верхней кромки пласта

h = .

Используя выражения (4) и (3), получаем

h =

Определив d, найдем избыточную плотность пласта

Σ = .

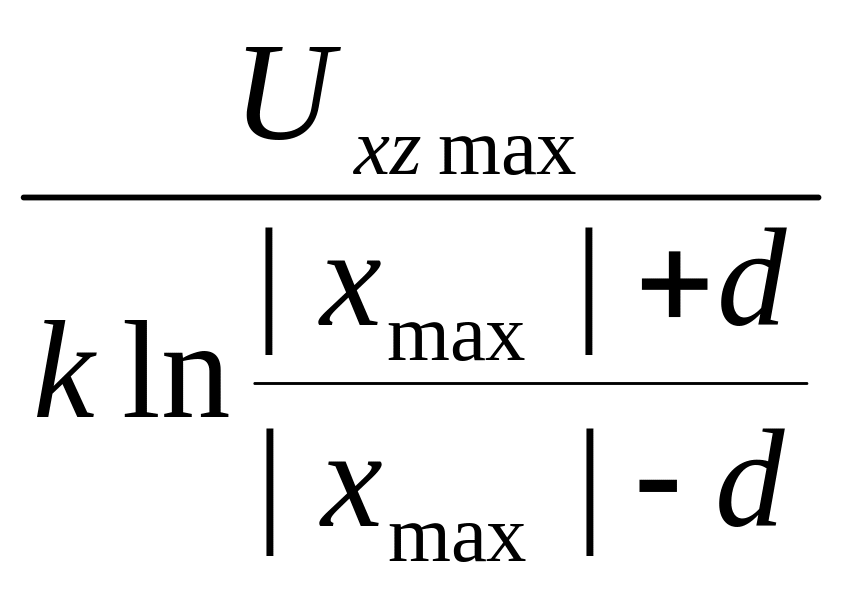Следует отметить, что параметры пласта находят без каких-либо предположений о каждом из параметров, так как контур пласта целиком определяется положением его угловых точек, являющихся особыми точками U_xz. Однако при этом следует иметь ввиду, что различные параметры пласта вычисляются с разной степенью надежности. Наиболее точно определяется h, менее точно d и σ. Особенно ненадежны определения d при 2d < h, так как в этом случае изменения горизонтальной мощности 2d можно компенсировать одновременным изменением σ так, что внешнее аномальное поле остается практически неизменным. При 2d ≤ h поле вертикального пласта идентично полю вертикальной материальной полосы и определение d невозможно без знания σ. Изменения же глубины h скомпенсировать изменением σ нельзя.