§ 12. Решение прямой и обратной задач для вертикального уступа

Вертикальным уступом называется тело бесконечного простирания, огра­ниченное двумя горизонтальными и одной вертикальной п лоскостью. Попе­речное сечение вертикального уступа представляет собой полубесконечную полосу со сторонами, параллельными координатным осям х и z. Геологическими аналогами вертикаль­ного уступа являются сбросы с кру­тым падением плоскости сбрасывателя, вертикальные контакты интрузий, со­ляных куполов, некоторые формы подземного и подводного рельефа и т. д. Для вывода формул гравитационного действия вертикального уступа воспользуемся следующими формулами для прямоугольного парал­лелепипеда бесконечного простирания:

U_z(0, 0) = ∆g(0, 0) = σk(ξln(ξ² + R²) + 2ζarctg ) ,

U_xz(0, 0) = σkln(ξ² + R²) ,

U_zz(0, 0) = 2σkarctg .

Обозначим через ξ горизон­тальную координату края уступа, h₁ и h₂ глубины верхней и нижней горизонтальных поверхностей, ограничивающих уступ. Положив в этих формулах ξ₁ = ξ, ξ₂ = ∞ получим формулы для вы­числения гравитационного эффекта вертикального уступа:

U_z(0, 0) = ∆g(0, 0) = σk(πζ - 2ζarctg - ξln(ξ² + ζ²)) ,

U_xz(0, 0) = σkln(ξ² + ζ²) ,

U_zz(0, 0) = 2kσarctg .

Перенеся начало координат в точку, расположенную над краем уступа, т. е. в точку (ξ, 0), и подставив пределы, найдем

U_z(x, 0) = ∆g(0, 0) = σk(π(h₂ – h₁) + 2h₂arctg - 2h₁arctg + xln ),

U_xz(x, 0) = σkln ,

U_zz(x, 0) = 2kσ(arctg - arctg ).

Анализ формулы U_z(x, 0) для вертикального уступа показы­вает, что

при x = .

Для симметричных точек

U_z(-x) + U_z(+x) = 2πkσH.

Rри­вые U_z(х, 0) для вертикального уступа и горизонтальной мате­риальной полуплоскости однотипны, если принять μ = σН. Таким образом, аномалия силы тяжести вертикального уступа может быть уподоблена с некоторым приближением аномалии силы тяжести материальной полуплоскости при условии, что глубина полупло­скости h = (h₂ + h₁)/ 2 и вся масса вертикального уступа скон­центрирована на этой полуплоскости.

Оценим погрешность, вызванную такой заменой. Для этого соста­вим отношение

ε = 1 - .

Очевидно, что величина относительной погрешности зависит от соотношений x/h и H/h, причем, чем больше H/h, тем больше величина погрешности при прочих равных условиях. Величина Н

может изменяться от нуля до 2h, при Н = 2h погрешность ε максимальна. Максимальная погрешность в самом н еблагоприятном случае, когда верхняя грань вертикального уступа выходит на поверхность Н = 2h, не превышает 0,072 при x/h = 0,25, при Н = h максималь­ная погрешность не превосходит 0,02. Следовательно, для определе­ния глубины залегания плоскости, расположенной посредине между верхней и нижней гранями вертикального уступа, можно поль­зоваться формулой, выведенной для горизонтальной материальной полуплоскости.

Полученные выводы справед­ливы только для кривой U_z, а для кривых U_xz и U_zz используются совершенно другие приемы интерпретации.

Формула U_xz для вертикаль­ного уступа аналогична формуле U_z для вертикальной материаль­ной полосы, если в последней заменить μ на σ. Таким образом, ис­пользуя кривую U_xz, параметры вертикального уступа можно вы­числить по формулам

h₁ = m - ,

h₂ = m + ,

σ = ,

где m = .

x_1/2, и x_1/4 - абсциссы точек наблюдений, в которых U_xz достигает значений соответственно U_{xz max}/2 и U_{xz max}/4.

Если избыточная плотность σ известна, то h₁ и h₂ можно найти, не прибегая к определению x_1/4. Поскольку

U_{xz max} = 2kσln и h₁h₂ = x²_1/2.

то, обозначив U_{xz ma}/2kσ = B, получим

h₁ = , h₂ = x_1/2 .

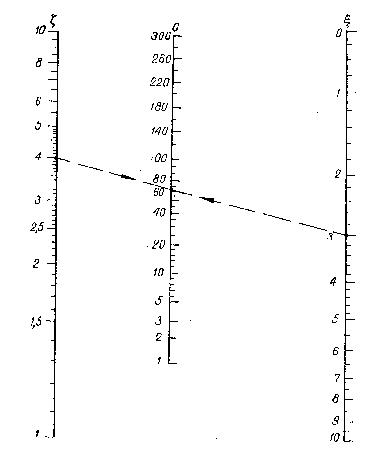Для вычисления аномалий U_xz вертикального уступа Д. Н. Хра­мов предложил номограмму. Для построения номограммы в исходную формулу введены обозначения ζ = h₂/h₁ и ξ = x/h₁ тогда

= kln .

Для вычисления U_хz по заданным значениям h₁, h₂ и х опреде­ляем ζ и ξ и находим их на крайних шкалах ζ и ξ. номограммы. Проводим через эти точки прямую и в пересечении ее со средней шкалой G снимаем величину U_xz/σ. Умножив ее на заданную вели­чину σ, получим значение U_xz.

Рассмотрим функцию U_zz(x, 0), определяемую уравнением

U_zz(x, 0) = 2kσ(arctg - arctg ) = 2kσ(φ₂ – φ₁) = 2kσΘ.

где Θ - угол, под которым из точки наблюдения видна вертикальная грань уступа.

П ри х = 0 и х = ±∞ функция U_zz = 0, при х >0 значения U_zz > 0, при х < 0 значения U_zz < 0. Абсциссы экстремальных значений

x_max = + , x_min = - ,

и функция

U_{zz max} = 2kσ(arctg - arctg ) = 2kσarctg .

Если σ известно, то введя обозначение tg = A, получим

h₁ = x_max( ,

h₂ = x_max( .

При неизвестном σ, чтобы определить h₁, h₂ и σ, необ­ходимо иметь еще одно уравне­ние. Для этого найдем x_1/2, при котором U_zz = U_{zz max}/2. В этом случае h₁ и h₂ можно найти путем простых геометриче­ских построений. Введем обозначения: Θ_mах - значение угла Θ в точке x_mах; Θ_1/2, Θ^/_1/4 - значения угла в точках x_1/2 и х^/_1/2. Точка х^/_1/2 лежит вправо от х_mах, в которой U_{zz max}/2. Очевидно, что Θ^/_1/2 = Θ_1/2 = Θ_mах/2.

Построим окружность 0₁, являющуюся геометрическим местом точек, из которых вертикальная грань уступа видна под углом Θ_mах, и окружность 0₂ - геометрическое место точек, из к оторых эта грань видна под углом Θ_1/2. Очевидно, что при Θ >0 имеется только одна точка, которой соответствует угол Θ_mах, это точка х_maх. Поэтому окружность O₁ касается оси х в этой точке, а следовательно, центр окружности лежит на перпендикуляре к оси х в точке х_mах. Точки x_1/2, и x^/_1/2, очевидно, находятся на концах хорды окружности О₂. Центр этой окружности лежит на перпендикуляре к оси х в точке х₀ = (x_1/2 + x^/_1/2)/2. Окружность О₁ касается этого перпендикуляра в центре окружности О₂, поскольку из точки O₂ вертикальная грань уступа видна под углом Θ _mах. Итак, имеем, что прямая х = x_max проходит через центр окружности О₁ а параллельная ей прямая х = х₀ = (x_1/2 + x^/_1/2)/2 касается окружности О₁. Отсюда следует, что радиус ρ₁ окружности О₁ равен х₀ – х_maх.

Таким образом, чтобы построить окружность O₁ необходимо: провести перпендикуляр к оси х в точке х_maх, отложить на нем отрезок, равный (x_1/2 + x^/_1/2)/2 – х_mах, и из полученной точки 0₁ как из центра провести окружность радиусом ρ₁. Точки пересечения этой окружности с перпендикуляром к оси х в начале координат определяют положение вертикальной грани уступа. Когда вели­чины h₁ и h₂ найдены, вычисляем σ.