6. Нормальное распределение силы тяжести

За нормальное значение распределения поля силы тяжести на поверхности Земли принимается поле сфероида вращения (сфероид вращения – это фигура Земли в первом приближении, так как геоид есть фигура не правильная и она не может быть описана математическими формулами).

Закон нормального распределения силы тяжести на поверхности сфероида (геоида) дает формула Клеро:

g = g_e(1 + βsin²φ), где

g_e – величина силы тяжести на экваторе, φ – широта точки, в которой определяется значение силы тяжести. Коэффициент β определяется по формуле, установленной Клеро: β = 5/2q – α, где коэффициенты q и α зависят от сжатия сфероида и определяются экспериментально.

При φ = 90⁰ получим значение силы тяжести на полюсе: g = g_e(1 + β). Откуда β = - есть относительный избыток силы тяжести на полюсе по сравнению с силой тяжести на экваторе.

Позднее была получена более полная формула для определения нормального значения силы тяжести – формула Гельмерта (1901 – 1909 гг.):

γ₀ = 978,030(1+0,005302sin²φ – 0,000007sin²2φ).

Этой формуле соответствует эллипсоид со сжатием α = 1/298,2. Формула Гельмерта была получена на основе около 1600 относительных измерений силы тяжести, распределенных по 9 широтным зонам.

В 1930 году на Международном геодезическом конгрессе в Стокгольме была принята в качестве международной формула Кассиниса:

γ₀ = 978,049(1+0,0052884sin²φ – 0,0000059sin²2φ).

Позднее некоторыми учеными были выведены и другие формулы для определения нормального значения силы тяжести, но широко используются только две из них – формулы Гельмерта и Кассиниса.

7. Вековые и периодические изменения силы тяжести.

Сила тяжести не может оставаться постоянной с течением времени, так как протекающие геологические и геофизические процессы в Земле приводят к перераспределению масс внутри Земли. Постоянно меняется положение Земли относительно Луны, Солнца и других небесных тел - это тоже оказывает влияние на изменение силы тяжести.

Изменения силы тяжести можно подразделять на периодические, связанные с вращением Земли вокруг свой оси (меняется положение Земли относительно Луны, Солнца и других небесных тел) и непериодические (вековые), создаваемые геологическими и геофизическими процессами, протекающими в Земле.

В настоящее время трудно судить о действительной величине вековых вариаций силы тяжести, поскольку отсутствует сколько-нибудь достоверный экспериментальный материал. А имеющиеся по этому вопросу данные лежат в пределах точности наблюдений и могут быть объяснены погрешностью измерений.

О существовании вековых вариаций силы тяжести можно говорить на основе теоретических предположений и некоторых косвенных наблюдений. Прежде всего следует отметить, что неотектонические движения вызывают значительные изменения высоты отдельных точек земной поверхности. Материалы повторных нивелировок убе­дительно показывают, что для отдельных районов вертикаль­ные перемещения земной поверхности могут достигать не­скольких сантиметров в год. Изменение высоты точки наблю­дения на 1 м приводит к изме­нению силы тяжести на 0,2 мгал, что вполне доступно для из­мерения современными грави­метрическими приборами. Вну­три Земли могут происходить чрезвычайно медленные пере­мещения масс и изменения их плотности, которые могут соз­давать заметные

вариации силы тяжести. Действительно, если в слое мощностью 100 км плот­ность изменится на 0,001 г/см³, то это приведет к изменению силы тяжести на 4 мгал, что вполне может быть установлено повтор­ными измерениями силы тяжести. В настоящее время проводятся экспериментальные наблюдения по выявлению вековых вариаций силы тяжести.

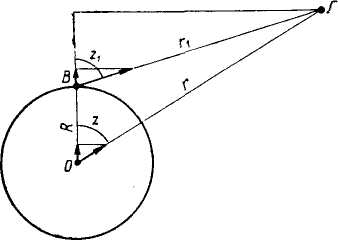
Периодические изменения силы тяжести в основном вызываются изменением положения Земли относительно Луны и, в меньшей степени, Солнца. Величину этих изменений можно вычислить сле­дующим образом. Пусть точка Л - Луна; В - точка наблюдения на поверхности Земли; О - центр тяжести Земли. Считая, что центр тяжести Земли в течение суток испытывает одинаковое притяжение, периодические изменения силы тяжести, вызванные Луной, будем определять как разность значений силы тяжести на поверхности и в центре Земли.

Введем следующие обозначения: М_л - масса Луны; r₁ и r - расстояние ее центра тяжести от пункта наблюдений В и от центра тяжести Земли; z₁ и z - зенитные расстояния центра Луны для пункта наблюдений и для центра Земли; R - радиус-вектор из центра Земли О в пункт наблюдений В. Напишем выражения для

Проекции притяжения Луны в точке наблюдения В и в центре Земли О на направление R: cos z₁; cos z₂.

Тогда периодическое изменение силы тяжести ∆g выразится разностью: ∆g = kM_Л( .

Проведя преобразования и исключая из этой формулы z₁ и r₁, получим выражение: ∆g = kM_Л (cos²z - 1). Аналогичная формула может быть получена и для Солнца.

Если принять, что М_Л = М_З; М_С = 332000М_З; r_{ср. Л} = 60,3R_З; r_{ср. С} = 23460R_З; М_З = ; g_ср = 980 гал.

Тогда при z = 0 получим

∆g_{max Л} = 0,12 мгал; ∆g_{max С} = 0,05 мгал.

Значения ∆g вычислены при условии, что Земля является абсолютно твердым телом. На самом деле Земля обладает некоторой пластичностью и под влиянием притяжения Луны и Солнца деформируется. В упругой твердой оболочке Земли возникает приливная волна, которая смещает точку наблюдения В от центра Земли и тем самым увеличивает величину вариаций силы тяжести приблизительно в 1,2 раза. Высокоточные гравиметрические наблюдения показывают, что лунносуточные вариации на 15 – 20% больше, чем вычисленные по вышеприведенным формулам.