3. Вторые производные потенциала притяжения и их физический смысл

Первые производные потенциала притяжения U по х, у и z есть проекции силы притяжения на эти оси.

Поскольку потенциал U есть функция трех независимых переменных, то он имеет шесть вторых производных:

, , , , , или

U_xx, U_yy, U_zz, U_xy, U_yz, U_xz.

Производные U_xx, U_xy, U_yy определяют форму уровенной поверх­ности в данной точке. Возьмем на этой поверхности точку О и примем ее за начало координат, ось z направим по нормали к уровенной поверхности. В этом случае координатная плоскость хОу будет касательной плоскостью к уровенной поверхности в точке О. Если через нормаль к уровенной поверхности провести ряд плоско­стей, то получим несколько так называемых нормальных сечений уровенной поверхности, каждое из которых будет плоской кривой. φ - угол, составленный какой-либо из секущих плоскостей с координатной плоскостью xOz.

Положив φ = 0 и π/2 получим нормальные сечения, совпадающие с координатными плоскостями xOz и yOz. Среди бесчисленного множества нормальных сечений имеются два сечения, которые обладают минимальной и максимальной кривизной. Эти сечения называются главными нормальными сечениями. Азимуты этих сечений определяются по формуле:

t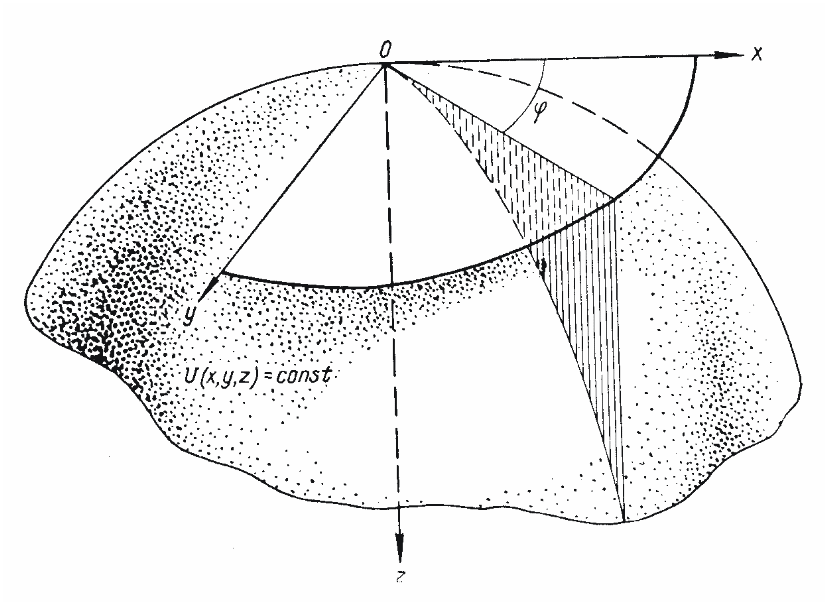 g2φ₀ = - , где U_∆ = U_yy – U_xx.

Два значения угла φ₀ отличаются на π/2.

Величина R = называется вектором кривизны и характеризует уклонение данной уровенной поверхности от сферической. Для сферы R = 0. Величины U_∆ = Rcos2φ₀ и -2U_xy = Rsin2φ₀ называются составляющими вектора кривизны. Таким образом, производные U_xx, U_yy и U_xy определяют разность кривизн главных нормальных сечений уровенной поверхности и их азимуты.

Рассмотрим физический смысл вторых производных потенциала силы притяжения U_zz, U_xz и U_yz.

Производная U_zz может быть представлена следующим образом: U_zz = = .

Так как ось z направлена по нормали к уровенной поверхности, то U_zz есть производная силы притяжения по вертикали. U_zz назы­вается вертикальной составляющей градиента силы притяжения.

Две другие производные U_xz и U_yz могут быть представлены сле­дующим образом: U_xz = = и U_нz = = .

т. е. эти производные являются составляющими градиента силы притяжения в горизонтальной плоскости.

Геометрическая сумма этих векторов равна вектору , характеризующему величину и направление наибольшего изменения силы притяжения в горизонтальном направлении. Величина вектора определяется из равенства = .

Азимут относительно оси х определяется углом α: tg α = .

По известным значениям U_xz и U_yz или можно определить составляющую градиента силы притяжения по любому направлению в горизонтальной плоскости, проецируя вектор на это напра­вление.

Поскольку первые производные потенциала силы притяжения есть ускорения, имеющие размерность в системе СГС , а в системе СИ , то размерность вторых производных в системах СГС и СИ будет . Единица, равная 1·10^-9 , названа этвеш по имени венгерского физика Р. Этвеша, впервые построив­шего прибор для определения вторых производных. Если ускорение силы притяжения меняется линейно, то изменение ускорения в 0,1 мгал на расстоянии 1 км соответствует 1 этвешу.