§ 12. Статические гравиметры

Статическими гравиметрами, или просто гравиметрами, называются приборы, в которых действие силы тяжести на массу чувствительной системы уравновешивается деформацией упругого тела. Величина деформации упругого тела пропорциональна действующей на массу силе тяжести.

По принципу действия гравиметры являются пружинными весами, в которых вес уравновешивается пружиной, деформирующейся по закону Гука. По устройству чувствительной системы гравиметры подразделяются:

1. Линейные системы, в которых масса совершает

поступательные перемещения.

2. Вращательные системы, в которых масса совершает

вращательное движение в вертикальной плоскости вокруг некоторого центра вращения.

Гравиметры с поступательным перемещением массы. Уравнение равновесия такого гравиметра имеет вид

mg + τl = 0

где m - масса, τ - коэффициент упругости, 1 - полная деформация.

Чувствительность системы, т. е. отношение линейного смещения груза к расчетной точности измерения силы тяжести, будет равна или .

Из последнего соотношения видно, что для измерения силы тяжести с достаточной точностью необходимо измерять очень малые линейные смещения порядка долей микрона. Поэтому приходится применять различные оптические и электрические эффекты.

Большинство современных приборов относится к вращательному типу. В этих гравиметрах проще повысить чувствительность системы. Повышение чувствительности гравиметров называется астазированием.

Уравнение равновесия чувствительной системы гравиметра вращательного типа имеет вид: gM_m(α) + M_τ(α) = 0, где gM_m(α) - момент силы тяжести как функция угла поворота рычага системы; M_τ(α) - момент упругих сил как функция угла поворота системы.

Перепишем уравнение в виде g = -

продифференцируем и в результате получим

Это и есть основное уравнение гравиметра вращательного типа в дифференциальной форме. Для того, чтобы увеличить чувствительность гравиметра (отношение, стоящее в левой части уравнения), необходимо либо увеличивать числитель дроби, занимающей правую часть уравнения, либо уменьшать величину знаменателя этой дроби. Увеличение числителя можно сделать лишь путем увеличения размеров чувствительной системы гравиметра, что крайне нежелательно. Более предпочтительным является второй путь - уменьшение знаменателя. Необходимо чтобы слагаемые, стоящие в знаменателе, имели разные знаки. Второе слагаемое всегда положительно. Значит нужно, чтобы первое слагаемое было отрицательным. Для этого необходимо, чтобы функция М_т(α) была убывающей. Этого и добиваются при помощи астазирования.

Пример астазированной системы приведен на рисунке.

К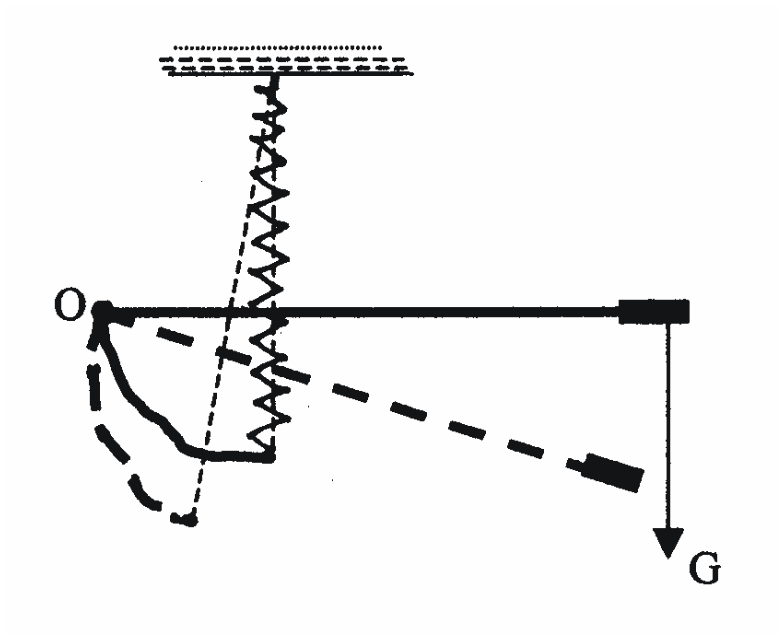 ак видно из рисунка, при наклоне рычага маятника плечо упругих сил уменьшается. Это значит, что вращающий момент упругих сил получает добавку при наклоне маятника под действием силы тяжести. При этом знак добавки противоположен знаку приращения силы тяжести. В самом деле при уменьшении силы тяжести маятник отклонится вверх и это вызовет увеличение плеча упругих сил и соответственно увеличение момента упругого противодействия.