5

Гравиразведка

(Курс лекций для геофизиков, 2010 СОФ ВГУ)

Литература

1. Миронов В.С. Курс гравиразведки. Л., «Недра», 1972. 512 с.

2. Маловичко А. К. Основной курс гравиразведки. Ч.1, Ч 2.

3. Успенский Д. Г. Гравиразведка.

4. Справочник геофизика том V. Гравиразведка.

5. Грушинский И. П., Грушинский А. Н. В мире сил тяготения. 1986 г.

6. Цубои Т. Гравитационное поле Земли. 1982 г.

7. Шимбирев Б. П. Теория фигуры Земли.

Введение

Поведение силы тяжести на земной поверхности начали изучать более двух веков назад. В настоящее время на Земле ежегодно про­водятся сотни тысяч новых определений силы тяжести в различных условиях (на суше и море, в подземных выработках и скважинах). Такое широкое распространение измерений силы тяжести связано с использованием их для решения ряда важнейших задач науки и практики, причем сфера приложения определений силы тяжести все время расширяется.

Большинство определений силы тяжести служит для изучения геологического строения исследуемых территорий, для поисков и раз­ведки полезных ископаемых, составляя основу одного из методов разведочной геофизики - разведочной гравиметрии.

Знание распределения силы тяжести на земной поверхности имеет огромное значение для геодезии, занимающейся изучением фигуры Земли. Гравиметрические измерения являются неотъемлемой частью геодезических исследований. В частности, по гравиметрическим дан­ным найти сжатие Земли значительно проще, чем по градусным измерениям.

Гравиметрические данные необходимо принимать во внимание при запуске искусственных спутников Земли, поскольку для точного расчета орбит спутников надо знать распределение силы тяжести на земной поверхности. С другой стороны, исследуя изменения орбит спутников, получают богатый материал для изучения гравитацион­ного поля Земли.

Знание абсолютного значения силы тяжести имеет большое зна­чение в метрологии, поскольку величина силы тяжести на экваторе является константой, необходимой при создании различных стандартов и установлении единиц измерения механических, магнитных и электрических сил. Например, единица силы тока ампер определяется как сила взаимодействия двух проводников опре­деленной конфигурации, возникающая при пропускании через них не изменяющегося тока. Сила взаимодействия проводников при этом уравновешивается весом mg известной массы m.

Знание абсолютного значения силы тяжести хотя бы в одной точке земной поверхности необходимо для приведения в единую абсолют­ную систему всех гравиметрических измерений на земном шаре, для изучения долгопериодических вариаций силы тяжести, получения параметров формулы нормального распределения силы тяжести. Точное знание g_e необходимо также для выражения массы Земли в метрических единицах, что позволяет приводить массы других небесных тел в таких же единицах, а не в единицах массы Земли.

1. Сила притяжения

Сила тяжести g в точке есть равнодействующая силы притяжения F Ньютона всей массы Земли и центробежной силы С, вызванной вращением Земли вокруг своей оси, т.е. g = F + C

П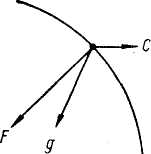 о сравнению с силой притяжения центробежная сила мала. Она не связана с распределением масс в Земле и ее можно вычислять.

Согласно закону всемирного тяготения Ньютона две точечные массы m и m₁, расположенные на расстоянии r одна от другой, вза­имно притягиваются с силой, модуль которой определяется по формуле: f = k , где k - гравитационная постоянная.

Численное значение k в системе СГС 6,67·10^-8 ; в системе СИ - 6,67·10^-11 . Сила притяжения, действующая на единичную массу называется напряженностью поля притяжения. Сила притяжения численно равна уско­рению, сообщаемому массе и отличается от ускорения только размерностью. Размерность силы притяжения в системе СГС - , размерность ускорения - . В точке с массой m₁ = 1 напряженность поля, обусловленного притяжением массы m, имеет величину F = k .

Напряженность поля притяжения в гравиметрии называется силой притяжения или притяжением. Для краткости термин «сила притяжения» сохраняется и за ускорением силы притяжения.

Сила притяжения представляет собой вектор, направленный от притягиваемой точки (с массой 1) к притягивающей точке (массе).

Единица измерения силы притяжения в системе СГС дина [ ], в системе СИ ньютон [ ].

Ускорение 1см/сек² = 1·10^-2 м/сек² в честь Г. Галилея названо гал. В практике чаще используют более мелкие единицы: миллигал (1 мгал = 1·10^-3 гал) и микрогал (1 мкгал = ·10^-6 гал).

Р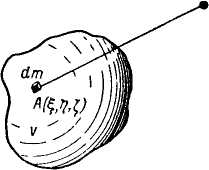 ассмотрим силу притяжения массы, распределенной в объеме

B(x, y, z) V с плотностью σ = σ(ξ, η, ζ). Поместим в

точку В с координатами х, у, z массу,

равную 1. В точке А с координатами ξ, η, ζ,

находящейся в объеме V притягивающего тела, выделим эле­ментарную массу dm.

Сила притяжения массы dm в точке В: dF = k , где

r = .

Проекции силы dF на оси х, у, z получим, умножив силу dF на косинусы углов, которые образует вектор dF с осями координат:

dF_x = dFcos(dF, x) = k · = k ;

dF_y = dFcos(dF, y) = k · = k ;

dF_z = dFcos(dF, z) = k · = k .

Сила притяжения F в точке В (х, у, z) всей массы, распределен­ной в объеме V, может быть найдена интегрированием выражений для dF_x, dF_y, dF_z по всему объему притягивающего тела. В результате получим составляющие силы F по осям х, у, z:

F_x = k ; F_y = k ; F_z = k ,

где dm = σdξdηdζ.

Выражения для F_x, F_y, F_z являются производными по х, у, z функции U = k , т. е. F_x = , F_y = , F_z =

Функция U обладает тем свойством, что ее частные производные по координатам притягиваемой точки равны составляющим силы притяжения по соответствующим осям координат. Функции, обла­дающие таким свойством, называются потенциальными. Функцию U называют потенциалом притяжения или гравитационным потенциалом.