4.3 Исследование непрерывной сау
Проведём моделирование системы автоматического управления средствами программного пакета MATLAB. Воспользуемся расширением данного программного продукта – средой моделирования Simulink. Используя встроенные средства среды Simulink, получим график переходного процесса системы, при воздействии на неё единичного ступенчатого сигнала (рисунок 4.2.).
Рисунок 4.2 Модель системы автоматического управления в среде Simulink
Рисунок 4.3 График переходного процесса системы при воздействии на неё единичного ступенчатого сигнала
Из графика можем определить следующие параметры система автоматического управления:
величина статической ошибки – 0,002 %;
время переходного процесса – 14 с;
колебательность отсутствует;
коэффициент перерегулирования – 0%.
Исходя из этих данных, можно сделать вывод о том, что система автоматического управления не соответствует техническому заданию (по пункту время переходного процесса) и нуждается в корректировке. В качестве корректирующего звена выберем ПИД (пропорционально-интегрально-дифференциальный) регулятор.
4.4 Настройка пид - регулятора
Для настройки ПИД регулятора – определения значений пропорционального, дифференциального и интегрального коэффициентов – воспользуемся встроенными средствами среды Simulink.
Подбор коэффициентов будем осуществлять с помощью блока NCD OutPort. Включим его в схему, как показано на рисунке 4.4.
Рисунок 4.4 Схема, собранная для настройки ПИД регулятора
Значения коэффициентов, полученных оптимизацией в блоке NCD OutPort:
Kp = 0.99
Ki = 2.96
Kd = 0
После корректировки переходная функция удовлетворяет техническому заданию (рисунок 4.5).
Рисунок 4.5 Реакция системы на единичное ступенчатое воздействие
Получены следующие характеристики:
1) Время переходного процесса – 0.479 с.
2) Количество колебаний – 0.
3) Коэффициент перерегулирования – 0.
4) Статическая ошибка –0.
4.5 Определение передаточных функций разомкнутой и замкнутой системы
Определим передаточную функцию разомкнутой системы:
Wраз = Wус (p) ∙ Wдвигателя (p) ∙ Wредуктора (p) ∙ WПИД-регулятора (p)
Определим передаточную функцию замкнутой системы:
Х
арактеристическое
уравнение замкнутой системы имеет вид:
=
0
=
0
4.6 Критерий устойчивости Гурвица
Этот критерий позволяет определить устойчивость САУ, если характеристическое уравнение замкнутой системы представлено в виде:
Формулировка критерия: чтобы САУ была устойчива, необходимо и достаточно, чтобы определитель Гурвица и его диагональные миноры имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения замкнутой САУ. При C0 > 0 для устойчивости САУ необходимо и достаточно выполнение условий:
;.
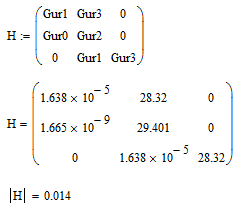
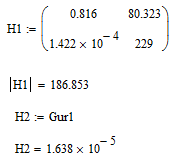
Определители диагональных миноров матрицы Гурвица больше нуля, следовательно, система устойчива.
4.7 Критерий устойчивости Найквиста
Критерий Найквиста – это частотный критерий, позволяющий судить об устойчивости САУ, замкнутой единичной обратной связью, по виду амплитудно-фазовой частотной характеристики разомкнутой системы.
Формулировка критерия: САУ устойчива в замкнутом состоянии, если годограф АФЧХ устойчивой разомкнутой системы не охватывает точки с координатами (-1, j0) на комплексной плоскости. Эта формулировка справедлива как для статических, так и астатических САУ, то есть систем, характеристическое уравнение которых содержит нулевой корень той или иной степени кратности.
Рисунок 4.6 Диаграмма Найквиста (АФЧХ)
Годограф АФЧХ устойчивой разомкнутой системы не охватывает точки с координатами (-1, j0) на комплексной плоскости (рисунок 4.6). Следовательно, система устойчива.