2.6 Исследование движения робота

Рассмотрим реализацию роботом одного прыжка под углом 45⁰ к горизонту при линии действия силы F₁₂, проходящей через центр масс объекта, м. По временным зависимостям рисунков 2.18 – 2.22 можно выделить пять этапов движения объекта: 1,4 – поворот относительно неподвижной точки А, 2 – плоскопараллельное движение с отрывом корпуса от поверхности под действием силы F₁₂, 3 – полет, 5 – статическое положение с двумя точками опоры. Первые два этапа происходят во время фазы разгона, третий соответствует фазе полета, четвертый и пятый – фазе приземления.

Рисунок 2.18 Графики перемещений вдоль оси Ох: – С, – А, – B, – D, – K

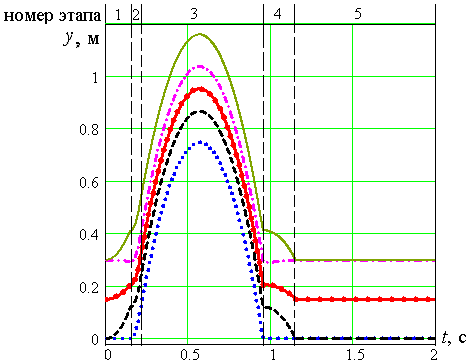
Рисунок 2.19. Графики перемещений вдоль оси Оу: – С, – А, – B, – D, – K

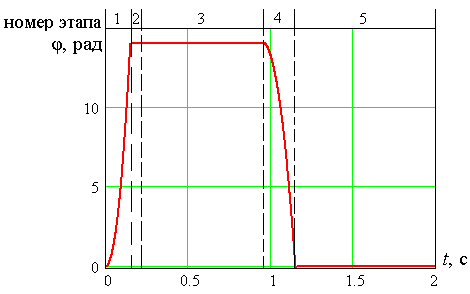
Рисунок 2.20 График угла поворота

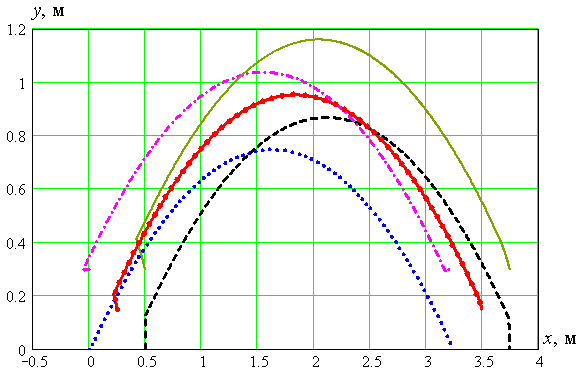
Рисунок 2.21 Траектории движения точек робота:

– С, – А, – B, – D, – K

На рисунке 2.22 показаны траектории движения центра масс робота при разных значениях силы F_12.

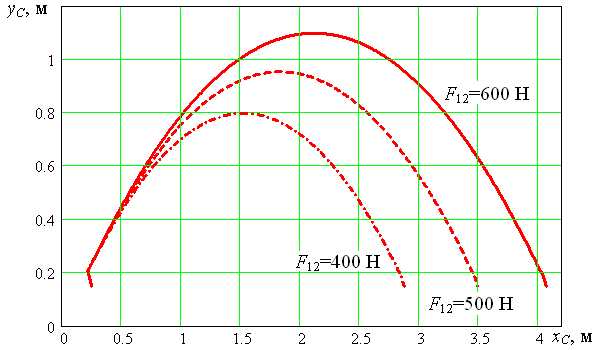
Рисунок 2.22 Траектории движения центра робота в зависимости от значения силы F₁₂

Для проектирования конструкции робота будем использовать результаты численного моделирования.

Длина полностью выдвинутой ноги l⁰= 0,15 м,

Сила, необходимая для реализации прыжка на высоту не менее 0,5 м, F₁₂=500 Н.

3 Расчетно-конструкторский раздел

Требуется разработать конструкцию ноги двуногого прыгающего робота, выполнить расчет приводов, обеспечивающих поворот звеньев ноги друг относительно друга и ноги относительно корпуса, а также привода линейного перемещения ноги.

3.1 Энергетический расчёт приводов

В соответствии с разрабатываемой конструкцией ноги прыгающего робота, описанной в п. 2.1, проведем расчет приводов, обеспечивающих ее позиционирование.

Энергетический расчет является важной частью процесса проектирования и направлен на рациональный выбор двигателя и преобразователя движения, которые обеспечивают заднные законы движения его выходного звена [2].

Чтобы узнать крутящий момент на валу электроприводов, необходимо рассчитать моменты инерции относительно осей их вращения.

3.1.1 Расчет привода поворота ноги относительно ступни

Схема для расчета привода, обеспечивающего поворот звеньев нога-стопа, показана на рисунке 3.1. Расчет будем проводить исходя из того, что угловая скорость вращения звеньев друг относительно друга должна быть равной 45 град/с.

Рисунок 3.1 Расчетная схема для выбора привода поворота ноги относительно ступни

Момент инерции равен:

,

где m_Н – масса ноги, кг;

L_Н – длина ноги, м.

Запишем выражение для определения выходного момента и подставим численные значения, получим:

где =10 рад/с²- угловое ускорение, рад/с².

Отсюда найдем момент на валу двигателя:

Из полученных данных найдем выходную мощность привода:

Рассчитаем необходимую мощность двигателя:

Исходя из рассчитанной мощности, выберем электродвигатель RE 6 фирмы Maxon, мощность которого составляет 0,3 Вт (рисунок 3.2).

Рисунок 3.2 Двигатель RE 6 фирмы Maxon

Характеристики двигателя приведены на рисунке 3.3.

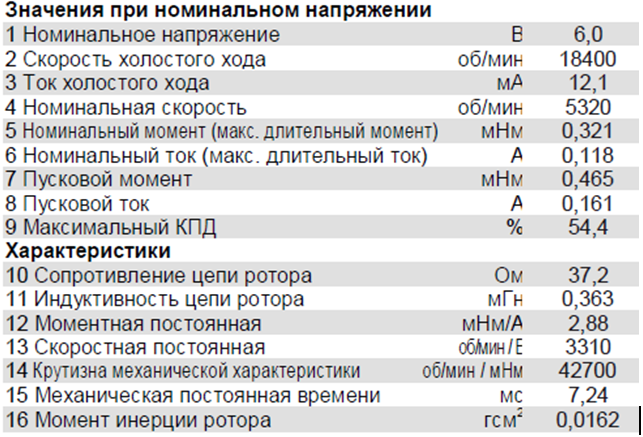
Рисунок 3.3 Технические характеристики двигателя RE 6

Для подбора редуктора к данному двигателю нам необходимо перевести скорость двигателя в рад/с: рад/с.

Рассчитаем передаточное отношение редуктора:

.

Из каталога был выбран редуктор планетарный редуктор GP 6 A, который совместим с двигателем, что обеспечивает простую сборку привода (рисунки 3.4, 3.5).

Рисунок 3.4 Размеры редуктора GP 6 A

Рисунок 3.5 Характеристики редуктора GP 6 A

Проверим выходной момент и угловую скорость полученного привода:

Данное значение полностью удовлетворяет требуемому.

3.1.2 Расчет привода поворота ноги относительно корпуса

Расчет привода, обеспечивающего поворот ноги относительно корпуса, проведем, исходя из требуемой угловой скорости вращения . Расчетная схема показана на рисунке 3.6.

Рисунок 3.6 Расчетная схема для выбора привода поворота корпуса относительно ноги

Уравнение момента инерции на валу будет иметь вид:

Рассчитаем значение радиуса инерции r_К:

Запишем выражение для определения момента на валу двигателя и подставим численные значения, получим:

Из полученных данных найдем выходную мощность привода:

Рассчитаем необходимую мощность двигателя:

Исходя из рассчитанной мощности, выберем электродвигатель RE 25 фирмы Maxon с мощностью 10 Вт, характеристики двигателя приведены на рисунке 3.7.

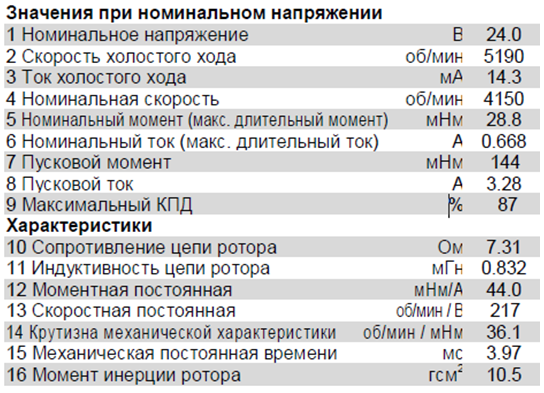
Рисунок 3.7 Технические характеристики двигателя RE 25

Для подбора редуктора к данному двигателю необходимо перевести скорость двигателя в рад/с: рад/с.

Рассчитаем передаточное отношение редуктора:

Из каталога был выбран редуктор планетарный редуктор GP 26 В диаметром 22 мм, который совместим с двигателем, что обеспечивает простую сборку привода (рисунки 3.8, 3.9).

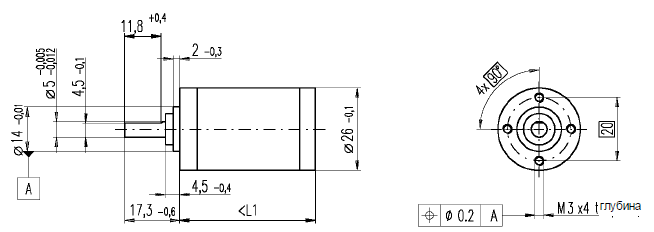
Рисунок 3.8 Размеры редуктора GP 26 В

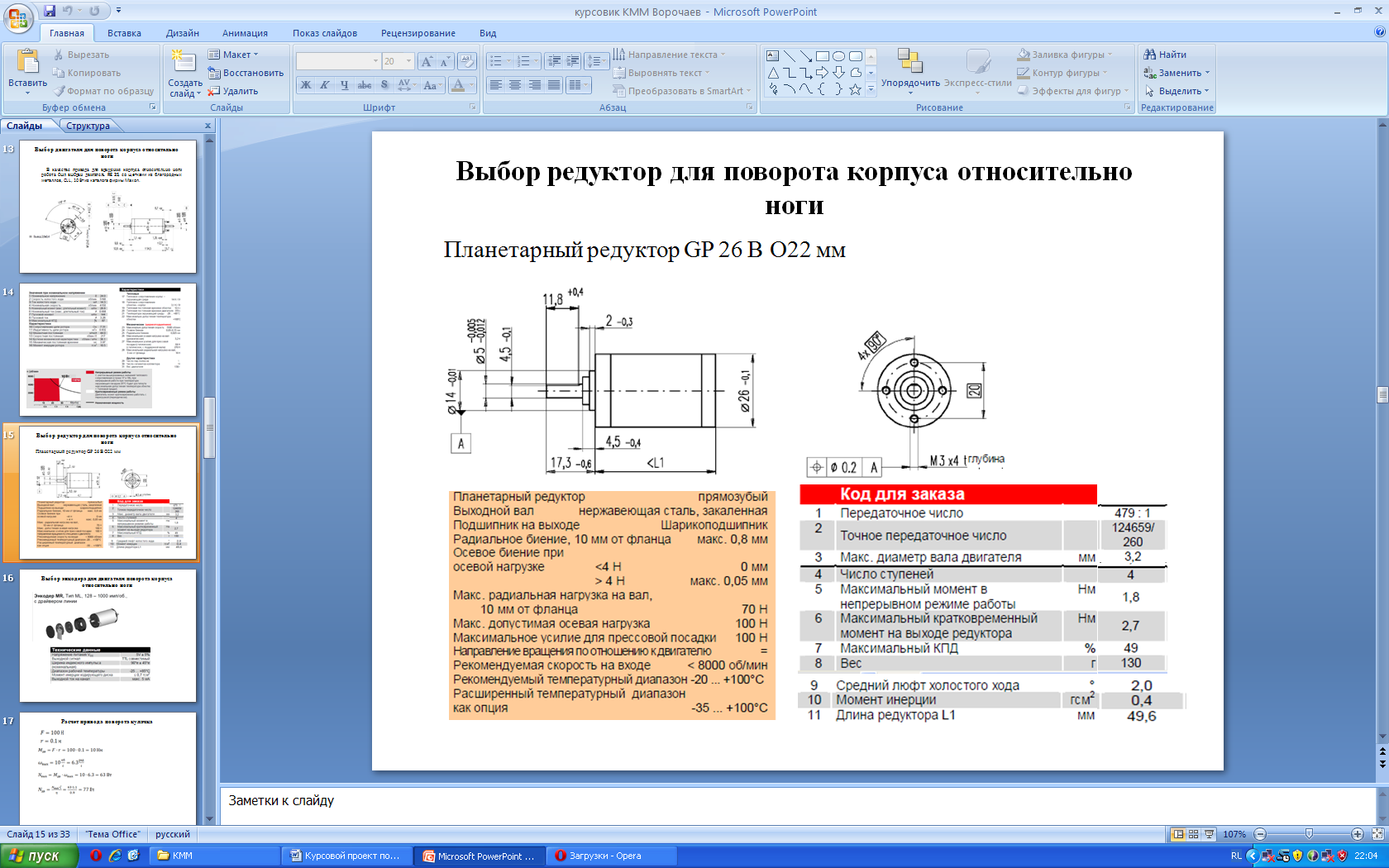
Рисунок 3.9 Характеристики редуктора GP 26 В

Проверим выходной момент полученного привода:

Проверим угловую скорость на выходе:

Данные значения полностью удовлетворяют требуемым.

3.1.3 Расчет электропривода поворота кулачка

В соответствии с результатами математического моделирования для реализации прыжка на высоту не менее 0,5 м необходима сила 500 Н. Примем, что кулачок за счет угла подъема профиля дает выигрыш в силе в 5 раз, поэтому будем рассчитывать привод, создающий силу F=100 H. Требуемая угловая скорость на выходе привода составляет

1 об/с

Исходя из этого, запишем уравнение для момента на валу двигателя:

где r=0,1 м – максимальный радиус кулачка.

Из полученных данных найдем выходную мощность привода:

Рассчитаем необходимую мощность двигателя:

В соответствии с определенной мощностью выберем электродвигатель RE 35 90 Вт из каталога фирмы Maxon, рисунок 3.11.

Рисунок 3.11 Технические характеристики двигателя RE 35

Рассчитаем передаточное отношение редуктора:

Выберем планетарный редуктор GP 32 A, который совместим с двигателем, что обеспечивает простую сборку привода (рисунки 3.12, 3.13).

Рисунок 3.12 Размеры редуктора GP 32 A

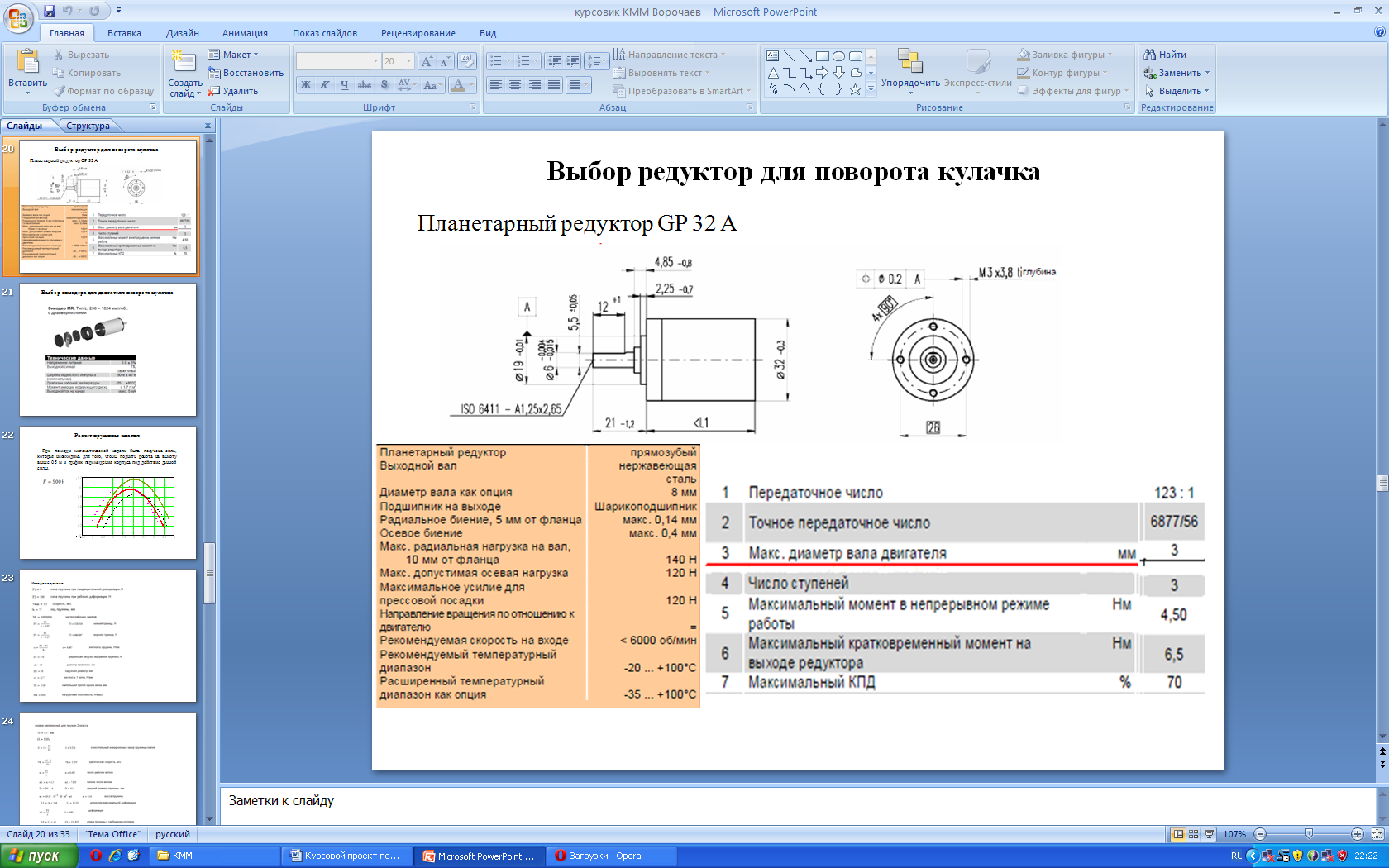
Рисунок 3.13 Характеристики редуктора

Проверим выходной момент полученного привода:

Проверим угловую скорость на выходе:

Данные значения полностью удовлетворяют требуемым.