Методи та системи штучного інтелекту
Лекція 5
Агломеративний ієрархічний
Кластерний аналіз.
5.1. Модель кластерного аналізу відредагувати
Традиційне формулювання задачі кластерного аналізу, як класифікації багатомірних кількісних та якісних даних полягає в наступному.
Нехай
– множина об’єктів, яку необхідно
розбити на
підмножин (кластерів)
так, щоб кожен з об’єктів
належав лише одному кластеру, причому
об’єкти які належать до одного кластера,
були “подібними”, а об’єкти які належать
до різних кластерів, були “відмінними”
між собою, причому саме розбиття повинно
задовольняти певним обмеженням і деякому
критерію оптимальності.
Для розв’язку цієї задачі розглядають
набір (множину)
ознак (властивостей, характеристик),
якими володіють об’єкти множини
.
Ознаки можуть бути як кількісними так
і якісними. За множиною ознак
,
кожному об’єкту
ставиться у відповідність
-мірний
вектор (точка)
,
де
– значення
-ої
ознаки об’єкта
.
Це дозволяє ототожнити за даним набором
ознак множину об’єктів
з деякою множиною
точок (векторів)
-мірного
простору. При цьому з рівності
випливає, що відповідні елементи
і
або дійсно ідентичні, або ідентичні за
даною множиною ознак
.
Поняття схожості об’єктів
визначають вибравши деяку функцію
,
яку називають мірою схожості або
подібності. В якості такої міри подібності
можна взяти будь-яку функцію
,
яка ставить у відповідність кожній парі
об’єктів
і
невід’ємне число
,
яке задовольняє умові:
,
причому
тоді і тільки тоді, коли
співпадає з
за даною множиною ознак, крім того має
місце рівність
.
Для визначення міри подібності спочатку
вводять поняття відстані
між об’єктами
і
.
Для цього вибирають яку-небудь метрику
в
-мірному
просторі, тобто деяку невід’ємну функцію
,
яка задовольняє наступним умовам:
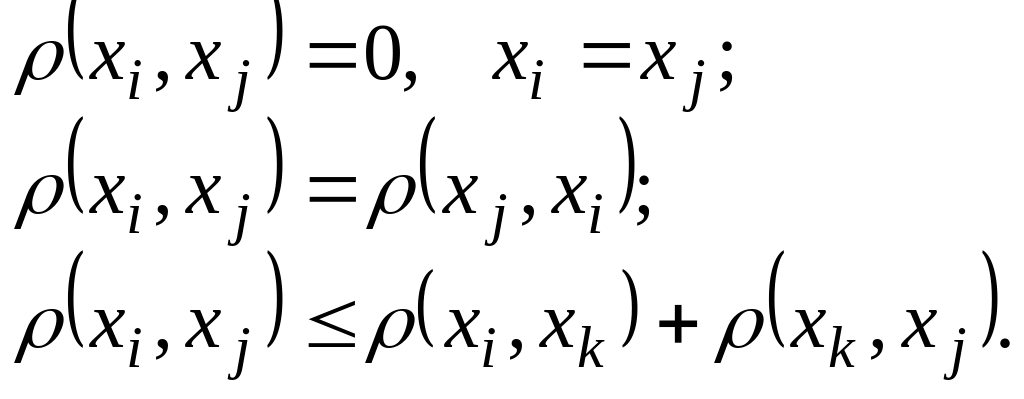
Відстань
між об’єктами
і
визначають як
,
де
і
точки
-мірного
простору, які ставляться у відповідність
об’єктам
з допомогою наборів ознак
.
Міру подібності між об’єктами
можна визначити наступним чином:
.
Оскільки, будь-яке розбиття множини
на кластери
зумовлює відповідне розбиття множини
на підмножини
(і навпаки), то відстань між кластерами
.
Діаметр кластера
.
Сукупність об’єктів
,
подібних (схожих) до об’єкта
,
або множина точок
,
які близькі до точки
,
визначають як множину
або відповідно
,
де
– додатне число, яке називають порогом
подібності. Об’єкт
вважають подібним до (схожим з)
,
якщо відстань
між цими об’єктами є меншою за поріг
подібності
.
Міру подібності і поріг подібності
вибирають з міркувань та представлень
про схожість об’єктів множини
.
Використовуючи введені поняття, математичну модель задачі кластеризації можна записати в такий спосіб.
Розбити множину на кластери так, щоб
.
Задача багаторівневої ієрархічної
кластеризації полягає в тому, що для
кожного
(
– рівень ієрархії,
– кількість таких рівнів) множину
необхідно розбити на неперетинні
підмножини (кластери)
таким чином, щоб діаметри кластерів
не перевищували заданих величин (порогів
подібності)
і при цьому були досягнуті екстремуми
деяких цільових функцій
.
Об’єкти кластеризації на першому рівні
ієрархії – це кластери
вихідної множини
;
на другому рівні ієрархії – кластери
першого рівня; на третьому – кластери
другого рівня і т.д. таким чином, кожен
об’єкт (кластер)
-го
рівня представляє собою деяку множину
об’єктів (кластерів) (
– 1)-го рівня, тобто
.
На кожному рівні ієрархії об’єкти
описують різними наборами ознак
і схожість об’єктів визначають різними
мірами подібності
,
які вибирають з представлень про
схожість об’єктів даного рівня.
Математична модель задачі ієрархічної кластеризації
.
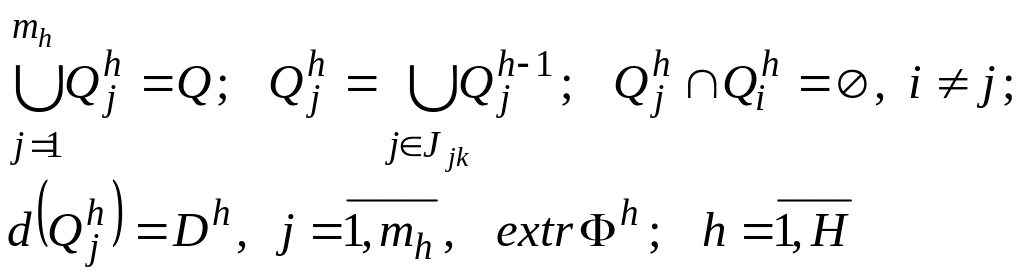Розв’язок задачі кластеризації суттєво залежить від вибору мір подібності і порогу подібності .