6. Найденный квант исключается из множества г, т.Е.

Г^(p+t) = Г^(p+t–1)|{G_p1}.

7. При выполнении условия

(i= : =I_m,

квант G_p1 (G_p–1,1) обозначается G_iVj и включается в ближайший кластер Г_j, т.е. V_j=V_j+ 1; Г = Г U{G_iVj}; t = t + 1, и переходим к п. 8, а в противном случае к п. 9.

8. Проверяется количество рассмотренных квантов. Если p + t  r, то переходим к п.13 (конец алгоритма), в противном случае к п. 5.

9. Найденный квант включается в переходное множество Г, в котором накапливаются кванты, не вошедшие в уже сформированные кластеры, т.е.

Г = ГU{G_p-1,i}.

10. Если множество Г*  , то переходим к п. 5. В противном случае переходим к следующему пункту.

11. Среди сформированного переходного множества Г ищется квант G_j1, для которого выполняется условие

(G_j1  Г): .

Найденный квант G_j1 назначается центром нового кластера и переходим к п.13. В противном случае переходим к следующему пункту.

12. Сформированное множество Г объявляется множеством Г, то есть выполняется условие Г = Г, а p = p + 2, и переходим к п. 2.

13. Конец алгоритма.

Описанный алгоритм выполняет кластеризацию структур G_iГ с автоматическим выбором количества кластеров s, где 2sr. В любой момент выполнения алгоритма 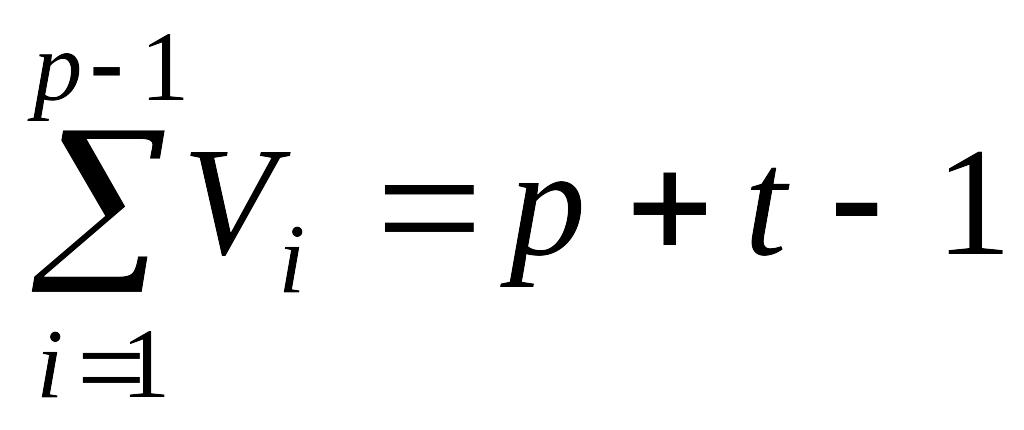. В конце алгоритма s=p, а . Преимуществом алгоритма является кластеризация без повторного пересмотра элементов.

Задача 5.3. Реализовать алгоритм формирования переменных модели измерения.

Решение задачи

Для формирования ММИ целесообразно использовать алгоритм (рис. 5.4):

1. Устанавливаются начальные значения j = 1, r = 1.

2. Из множества связей рассматриваемого кластера Г_m выбирается первая связь q_j  .

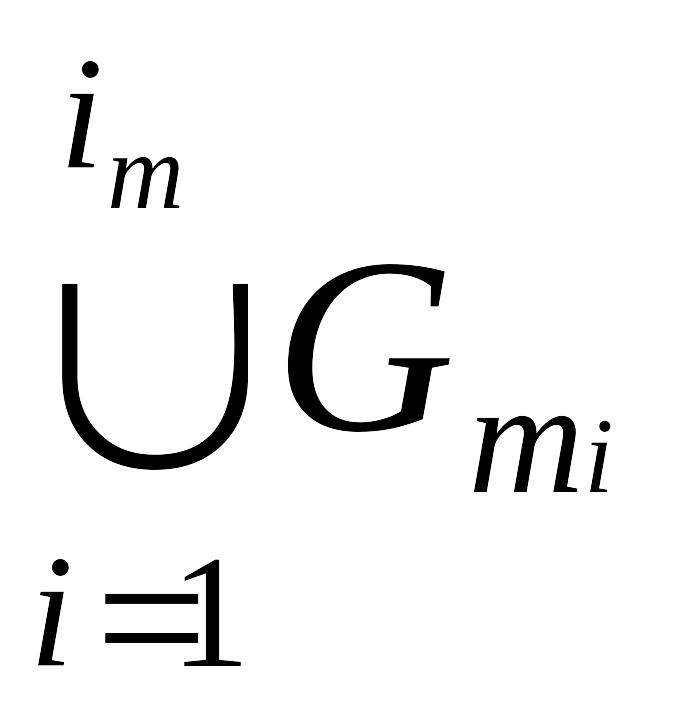3. Выбранная связь исключается из всех списков связей, представляющих структуры Q_miГ_m, т.е.

(i = ): Q = Q {q_j}.

4. Определяется риск использования выбранной связи в моделе измерения и при условии R_qi>R_доп, то j=j + 1 и переходим к п. 2. В противном случае рассматриваемая связь q_j включается в множество Q , представляющее типовую структуру G_m, т. е.

Q = Q .

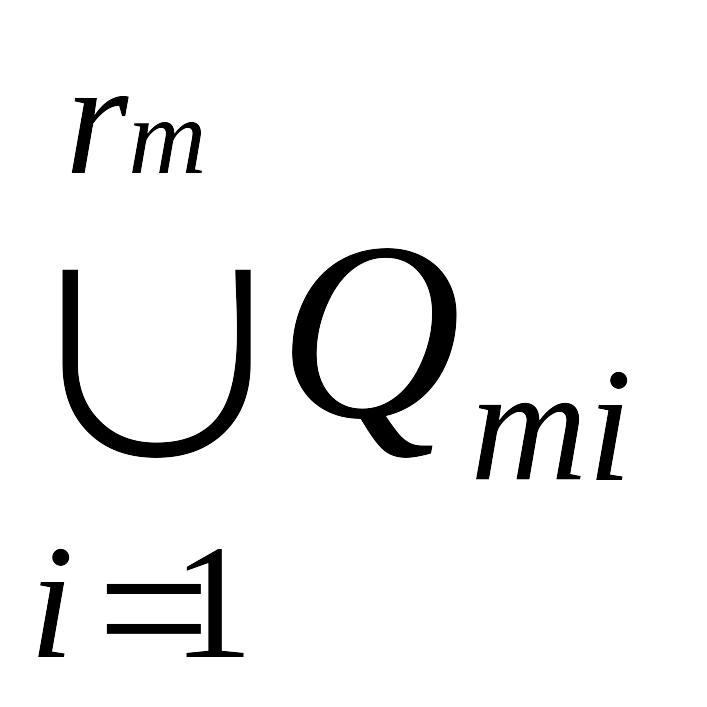
5. Если  (П_Мдоп–П_Мi<), то r=r+1, и переходим к п.1.

6. В противном случае, определяется риск сформированной модели R_M. Если R_M>R_Mдоп, то переходим к п.3 алгоритма множества максимально различающихся квантов. В противном случае переходим к п.7.

7. Конец алгоритма.

В результате выполнения алгоритма за Q  итераций получается типовая структура G (X ) кластера Г_m в виде списка упорядоченных квантов. Множество типовых структур является объединением X = .

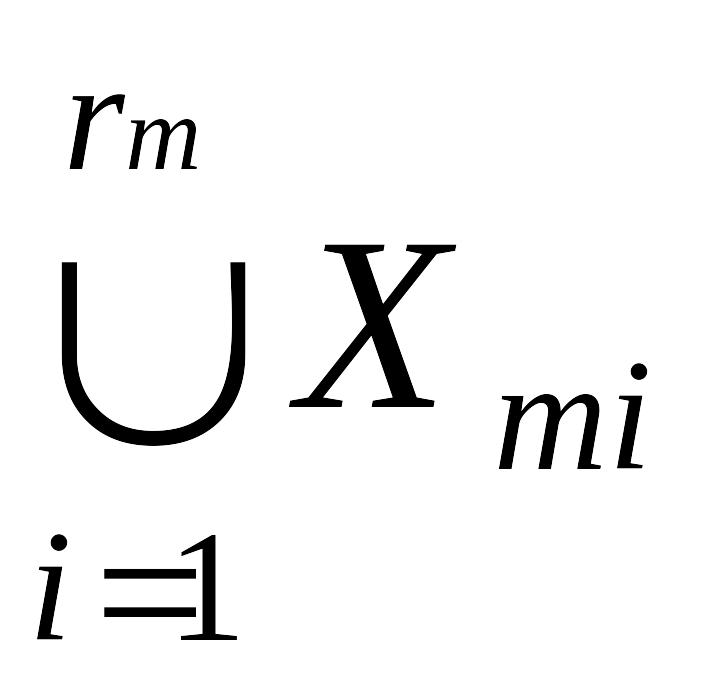Задача 5.4. Сформулировать алгоритм постановки начального эксперимента.

ВВОД

j = 1; r = 1

q_j

Q_mi^(j) = Q_mi^(j-1){q_j}

j = j + 1

Q_mi*^(j) = Q_mi*^(j-1){q_j}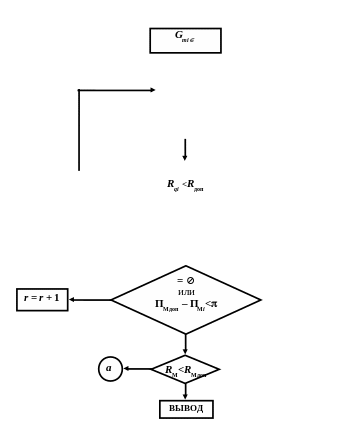

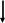
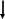
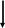
Рис. 5.4. Алгоритм формирования модели измерения на базе кластеров Г_М

Решение задачи

Введенные определения и полученный критерии формирования спектра эксперимента и различия позволяют синтезировать следующий алгоритм управляемого эксперимента. Пусть известно пространство S, множество M, графики функций b_Ai(u(y), ), b_Bi(u( ), ), b_Сk(u) и известно также эталонное пространство M^э, построенное на этапе обучения системы измерения. Зададим на парах элементов s_ij  M и s_ij^э  M^э функцию расхождения J(s_ij, M^э), тогда действие алгоритма управляемого эксперимента заключается в следующем:

1. В соответствии с пунктом 3 проведенного выше построения, определяется положение области s_ij в пространстве M по формулам для математического ожидания при равномерном законе распределения случайной величины:

A_i = 0,5( ) и B_j =0,5( ),

где x⁺ и x^– – наибольшее и наименьшее значения случайной величины выборки.

2. Выбирается конкретное управляющее воздействие, соответствующее величине математического ожидания для равномерного закона распределения:

C_i = 0,5( ).

3. Находится минимальное значение критерия расхождения для равномерного закона распределения в виде:

I(s_ij, M^э) = ln[S_i(C_i – C_i0)/(A_i – A_i0)],

где C_i0, A_i0 – начальные значения интервалов анализа соответствующего параметра, S_i – функция чувствительности на i-м интервале функции преобразования контролируемого объекта.

4. По результату п. 2 определяется подмножество значений C_kU.