Типовые задачи и примеры их решения
Задача 5.1. Реализовать алгоритм выбора множества максимально различающихся квантов Г*.
Решение задачи
Итеративный алгоритм выбора множества Г* (рис. 5.2) состоит из этапов:
1. Устанавливается количество необходимых максимально отличающихся квантов Г*, т.е. количество элементов множества Г*. При этом необходимо учитывать неравенство r Г0, а также вычислительные ресурсы (память и машинное время), имеющиеся для синтеза, отбора и структурного анализа вариантов.
2. Формируется первое приближение Г(i), i = 1 множества Г, в которое включаются первые r2 элементы множества Г0.
3. Устанавливаются начальные значения счетчика рассмотренных квантов t=0, порогового значения степени различия 0=0, а также константа , задающая необходимую точность расчетов.
4. Вычисляется средняя степень различия i квантов множества Г(i):
i
=
,
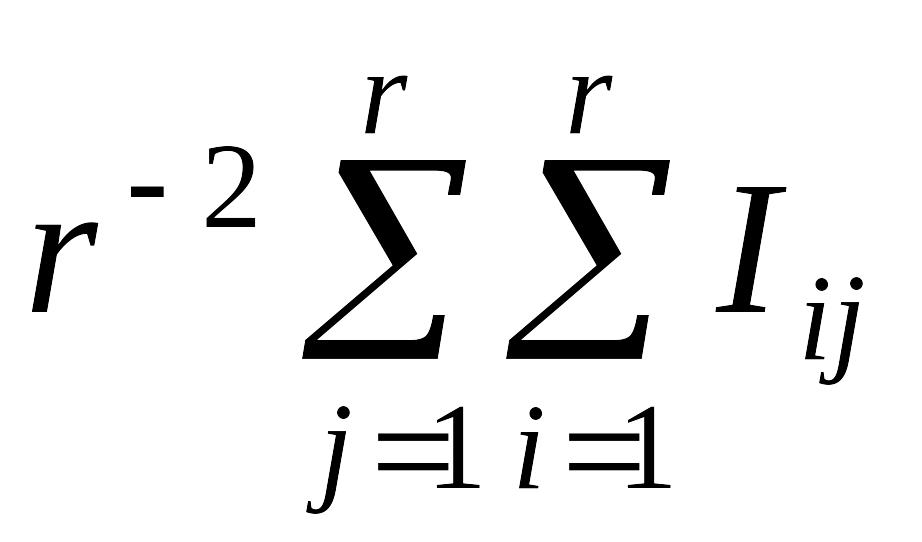i
j.
2.
5. Если i – i–1 < , то переходим к п. 10 (конец алгоритма).
6. Увеличивается значение t = t + 1 для рассмотрения следующего элемента множества Г0, которое обозначается Gr+t.
7. Если r + t Г0 или израсходовано машинное время, отведенное для выбора вариантов квантов, то переходим к п. 10 (конец алгоритма).
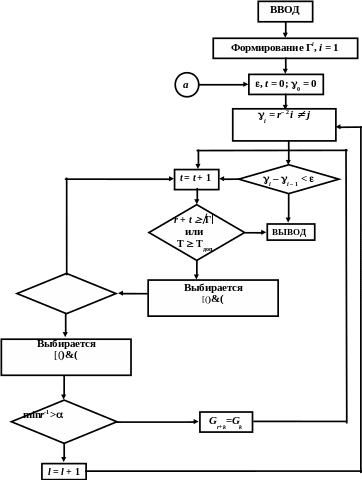
Рис 5.2. Алгоритм формирования множества максимально различающихся квантов
8. Квант Gr+t попарно сравнивается со всеми квантами Gi Г(i) по выражению (5.1). Если выполняется условие
[(Gr+t
)(
Gi
Г(l))]:
,
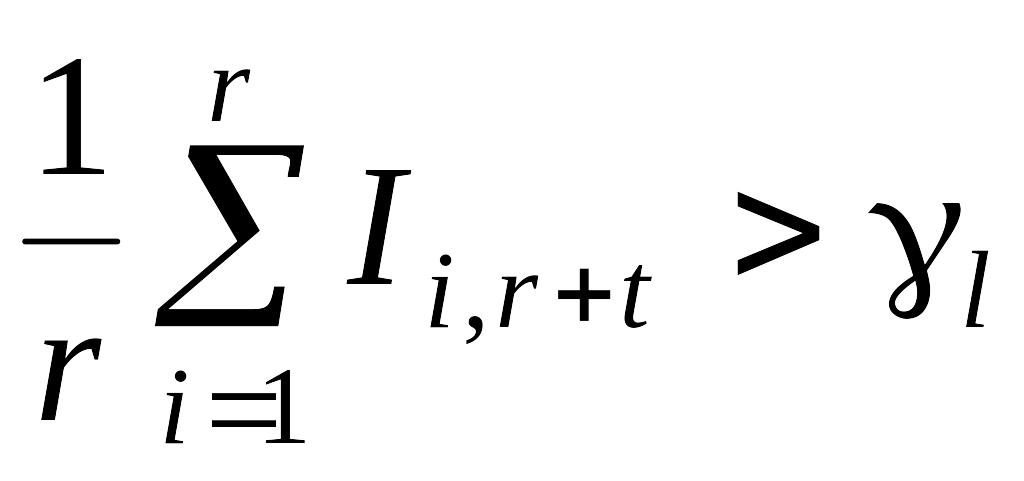где – дополнение Г(l) до множества Г0, то переходим к следующему пункту. В противном случае – переходим к п. 6.
9. В множестве Г(i) находится квант Gk, который максимально подобен остальным элементам множества Г(i), т.е. Gk, для которого выполняется условие
[(Gk
Г(i))
(
Gi
Г(i))]:
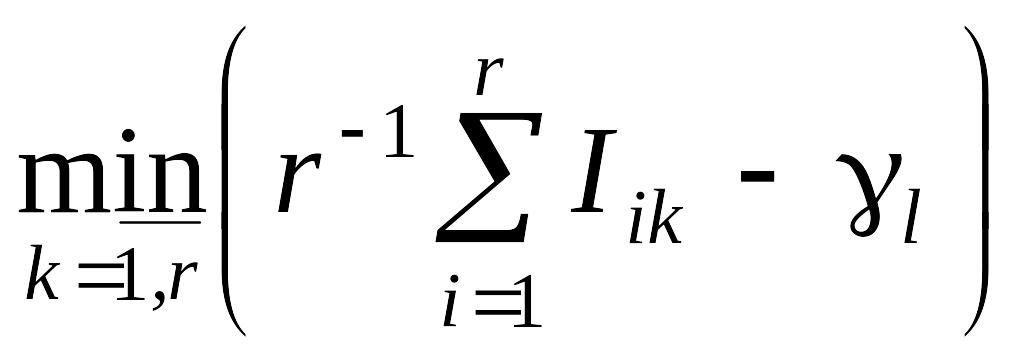<0.
Если квант Gk найден, то в дополнение Г(l) вместо него включается квант Gr+k и осуществляется переход к п. 6. В противном случае получено (l +1)-е приближение Г(l+1) множества Г, поэтому увеличивается l = l + 1 и осуществляется переход к п. 4.
10. Конец алгоритма.
В данном алгоритме постепенно увеличивается пороговое значение степени подобия l, которое используется для принятия решения при отборе вариантов квантов. Прерывается выполнение алгоритма в любой момент времени. При этом в множестве Г(i) содержатся наиболее различающиеся кванты из r + t квантов, рассмотренных до момента прерывания.
Задача 5.2. Реализовать алгоритм кластеризации квантов.
Решение задачи. На рис. 5.3 приводится алгоритм максиминного расстояния, предназначенный для кластеризации допустимых вариантов формирования областей определения X исходной области значений Y:
1. Устанавливаются начальные значения вектора текущего количества элементов кластеров = 0, текущего количества кластеров p = 2 и количества кластеризованных квантов, не являющихся центрами кластеров t = 0. Подмножества Гi Г в начале алгоритма пусты и постепенно пополняются квантами из множества Г.
2. В множестве Г* ищется пара квантов Gp1, Gp–1,1, для которой:
[(Gp1
Г*)
(Gp–1,
1
Г*)]: I(Gp1,
Gp–1,1)
=
,
где I(Gi, Gj) – расстояние между квантами Gi и Gj определяемое по выражениям (5.1, 5.2).
Г(Vp-1)
= Г(Vp-1)-1U{Gp1/Gp-1,1}
minI(Gp1/Gp-1,1;Gi)<
<0,5(p-1)–2
= Im
ВВОД
[(
Vj=Vj+1
ВЫХОД
Г(p+t)
= Г(p+t
– 1){Gi1}
Г(Vp)=
Г(Vp)
-1U{Gp1}
Г(Vp)
= Г(Vp)
-1U{Gp-1,1}
Г*(p+t)
= Г*(p+t-1){Gp,1}
Г*(p+t)
= Г*(p+t-1){Gp-1,1}
V
=
0; p
= 2; t
= 0
Г*
Г'
= Г'U{Gp-1,i}
Г =
Г'
p
= p +2
=
&(
]:
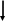
I(Gp1,
Gp-1,1)
=
I(Gi,
Gj)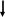
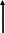
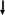
Рис. 5.3. Алгоритм кластеризации квантов
3.
Найденные
кванты назначаются центрами для двух
первых кластеров Г1
и Г2,
т.е. формируются текущие варианты
множеств
,
и
на базе предыдущих их вариантов
,
и
по выражениям
Vp–1=Vp–1+1;
=
|{
};
=
U{Gp–1,1}.
4.
Vp=Vp+1;
=
U{Gp1};
p=p+1.
5. Среди оставшихся элементов множества Г ищется квант Gp1, для которого выполняется условие
(Gp1
Г):
.