Типовые задачи и примеры их решения

Задача 3.1. Синтезировать алгоритм обработки сигнала для определения места повреждения высоковольтных кабельных линий.

Описание предметной области. Одним из путей повышения эксплуатационной надежности электрических сетей является быстрое выявление и восстановление поврежденных участков линий электропередачи. Протяженность распределительных сетей 0,4 – 35 кВ достигает нескольких миллионов километров. В условиях промышленных предприятий и городов до 80% электроэнергии доставляется потребителям по кабельным линиям. По данным эксплуатации кабельные линии повреждаются в 2–3 раза чаще, чем другие элементы цепи электроснабжения. Ежегодно в кабельных сетях отыскивается около полумиллиона мест повреждения. Время ликвидации таких повреждений составляет от нескольких часов до нескольких суток.

В комплексе мероприятий, связанных с выявлением повреждения кабельной линии, поиск места повреждения непосредственно на трассе линии остается одной из наиболее трудоемких операций. Большое разнообразие видов повреждений (замыкание одной, двух, трех жил между собой и на оболочку, обрыв жил, заплывающие пробои) и параметров поврежденной кабельной линии (переходное сопротивление, длина линии до места повреждения и за ним, марка кабеля и глубина его залегания) вызвало создание различных методов и устройств для непосредственного отыскания места повреждения на трассе кабельной линии. Однако ряд повреждений, прежде всего металлические однофазные замыкания и заплывающие пробои при неразрешенной оболочке, а также повреждения в кабелях с отдельным металлическим покрытием жил остаются еще трудно выявляемыми и требуют дополнительных теоретических оценок и получения на их основе новых технических решений как в части разработки новых способов поиска повреждений, обладающих большей разрешающей способностью в различных ситуациях, так и в части совершенствования аппаратуры.

Для совершенствования поисковой аппаратуры следует иметь необходимый расчетный аппарат при выборе параметров поисковой аппаратуры с учетом характеристик поврежденной кабельной линии, оценить помехозащищенность, чувствительность и в конечном итоге – надежность выявления повреждения и массогабаритные показатели аппаратуры, что позволяет повысить эффективность работы оператора и в целом снизить затраты и время на поиск места повреждения кабельной линии.

Примером поискового устройства являются акустические приемники, которые выпускаются в составе универсальных серийных кабелеискателей и предназначенные как для индукционного, так и для акустического метода определения места повреждения кабельных линий [В. В. Платонов, В. Ф. Быкадоров. Определение мест повреждения на трассах кабельной линии. – М.: Энергоатомиздат, 1993. – 256 с.]. Эти кабелеискатели различаются в основном типом акустического датчика, поэтому рассмотрим особенности выполнения кабелеискателей "Поиск" П-6 с электродинамическим микрофоном и КАИ-77 (КАИ-80) с пьезоэлектрическим датчиком и с цифровым измерителем расстояния.

Кабелеискатель "Поиск" содержит акустический и индукционный датчики с усилителями, которые через переключатель вида поиска могут подключаться к выходному усилителю с телефоном. В качестве акустического датчика может быть использован виброизмерительный пьезоэлектрический преобразователь типа ДН–3–М1, анализ которого приведен ниже в задаче 3.3, а в качестве индукционного датчика – катушка с сердечником, настроенная в резонанс на поисковую частоту.

Кабелеискатель КАИ-77 содержит пьезоэлектрический датчик со встроенным усилителем и встроенную в корпус прибора индукционную катушку, которые через усилитель приемника подключаются к головным телефонам. Предусмотрен выход на стрелочный индикатор. Кабелеискатель имеет ограниченную чувствительность по акустическому каналу.

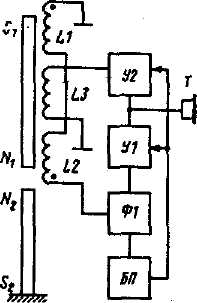
Повышенной избирательностью к заданному диапазону частот обладает кабелеискатель с электродинамическим датчиком и электромеханической положительной обратной связью (рис 3.2). Подвижный магнит NiSn, подвешенный в поле неподвижного магнита N₃S₃, при колебаниях грунта наводит в неподвижных катушках L₁ и L₂ противоположные по знаку ЭДС. Благодаря встречному включению катушек, полезный сигнал удваивается, а сигнал помехи вычитается. Суммарный полезный сигнал через полосовой фильтр Ф₁ и основной усилитель У₁ посту

Рис. 3.2. Структурная схема избирательного кабелеискателя с электродинамическим датчиком и электромеханической положительной обратной связью

пает на головные телефоны Т. Для уменьшения магнитострикционных помех корпус датчика выполнен из латуни, что несколько снизило полезный сигнал за счет снижения рассеяния магнита N₁S₁. Введение положительной обратной связи с выхода основного усилителя У₁ через усилитель обратной связи У₂ на катушку обратной связи L₃ существенно повышает чувствительность в рабочей полосе частот фильтра Ф₁ (100-1000 Гц). Общая чувствительность кабелеискателя 25 В с/м, масса 2,5 кг.

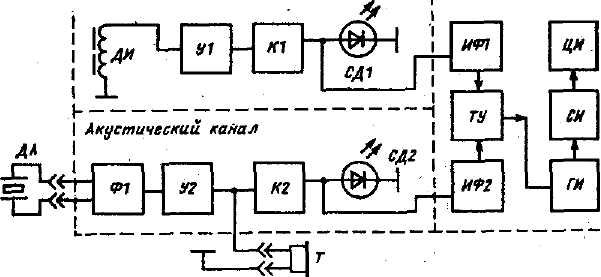
Индукционно-акустический кабелеискатель с цифровым измерителем расстояния позволяет быстро локализовать место повреждения за счет определения расстояния до источника электроакустических колебаний. Принцип работы измерителя основан на определении времени запаздывания акустического сигнала относительно индукционного сигнала, которое практически пропорционально расстоянию от оператора до места повреждения. Структурная схема кабелеискателя (рис. 3.3) – двухканальная, но сигнал индукционного канала используется в качестве опорного не только для измерителя расстояния», но и для контроля трассы и наличия разрядов.

Рис. 3.3. Структурная схема индукционо-акустического кабелеискателя ПА-02

Собственно приемник содержит аналоговую и цифровую части. К аналоговой части относятся акустический и индукционный каналы, а цифровая часть представляет собой двухразрядный счетчик тактовых импульсов, управляемый сигналами аналоговой части. Канал приема электромагнитного сигнала состоит из индукционного датчика ДИ, встроенного в корпус приемника, усилителя У₁, компаратора К₁ и светодиодного индикатора СД₁. Канал приема акустического сигнала содержит пьезоэлектрический датчик ДА, устанавливаемый на грунте, частотный фильтр Ф₁, усилитель-демпфер У₂, головные телефоны Т, а также компаратор К₂ и светодиодный индикатор СД₂. Измеритель расстояния содержит формирователь импульсного сигнала по индукционному ИФ₁ и акустическому ИФ₂ каналам, которые воздействуют на управляющий триггер ТУ, запускающий генератор тактовых импульсов ГИ. Счетчик импульсов СИ с цифровым индикатором ЦИ указывает расстояние до места повреждения.

Поиск места повреждения на трассе ведется следующим образом. Генератор акустических сигналов подключается к поврежденной кабельной линии. Оператор входит в зону поиска (измеритель расстояния выключен) и по индукционному каналу фиксирует трассу кабеля. Перемещаясь по трассе и периодически устанавливая акустический датчик на грунт, оператор находит зону приема акустического сигнала с помощью головных телефонов. Одновременно возникает синхронное мигание светодиодов индукционного и акустического каналов, что свидетельствует о возможности включения измерителя расстояния. Показания двухразрядного индикатора (от О,9 до 9,9 м) позволяют вести ускоренный целенаправленный поиск. Над местом повреждения прибор показывает глубину залегания кабеля.

Решение задачи

1. Системный анализ решаемой задачи и этап формализации постановки решаемой задачи. При традиционном подходе к задаче оценивания принимают соответствующие гипотезы о приближенных нормальности, независимости, однородности шумов, сопровождающих процесс измерения, и т.д.. Это позволяет при выборе алгоритма обработки информации использовать метод максимального правдоподобия [1], обеспечивающий минимизацию риска оценки результатов измерения.

Так для выборки Y = (Y₁,..., Y_n), каждый элемент Y_i которой имеет плотность распределения f(y_i; x), x  _x, плотность распределения выборки Y определяется выражением

f(y; x)= (y_i; x), y = (y₁,..., y_n)Rⁿ, x_x,

а функция правдоподобия данного вектора Y имеет вид

(Y; x) = f(Y; x) = (y_i; x), x_x.

При регулярном семействе F = {f(y; x), x  _x} для нахождения оценки максимального правдоподобия (Y) пользуются стандартными приемами дифференциального исчисления, решая уравнение правдоподобия

(Y; x) = 0.

При этом всякий математический результат, предназначенный для непосредственного практического использования, должен обладать свойством устойчивости по отношению к небольшим отклонениям от исходных предположений. Однако в ряде случаев даже небольшие вариации исходных предпосылок о вероятностной структуре контролируемой информации могут привести к существенному ухудшению свойств используемых процедур. Поэтому необходимо постоянно оценивать условия измерения и осуществлять адаптацию к ним.

При измерении влияние одной из компонент может настолько перевесить суммарный вклад других компонент в ln (Y; x), что ее значение будет полностью определять величину оценки. Сам по себе этот эффект не вызывает беспокойства, если модель для плотности вероятности верна, однако он может возникать и при случайном ошибочном измерении, который не описывается принятой плотностью распределения вероятности f, то есть в общем случае f задает только приближенную исходную модель. Характеристики номинально оптимальных процедур обработки сигналов во многих случаях могут резко ухудшаться, даже при сравнительно малых отклонениях от исходных данных. В этом состоит основная причина, по которой приходится строить алгоритмы обработки сигналов, которые характеризуются свойством робастности [7, 64], то есть алгоритмы, обладающие высокой эффективностью в условиях, когда свойства сигналов и шума могут меняться в пределах заданных классов возможных характеристик.

Наличие априорной неопределенности относительно статистических характеристик информации измерения приводит к необходимости построения методов обработки, обладающих пониженной чувствительностью к всевозможной неадекватности между априорно принятой вероятностной моделью и свойствами реальной среды, то есть робастностью.

Важнейший подход к проблеме синтеза робастных методов обработки, обеспечивающих достаточно точное решение подобных задач в условиях неопределенности, дает принцип минимакса. Минимаксный подход требует заранее ориентироваться на ситуацию, наименее благоприятную для задачи оценивания, т.е. обеспечивает получение некоторого гарантированного решения. Сущность подхода состоит в том, что, сохраняя высокую устойчивость найденных решений, он позволяет избежать значительного снижения точности оценивания в случае, когда условия оценивания близки к предполагаемым. Один из наиболее эффективных путей построения минимаксных алгоритмов дает метод максимального правдоподобия (или метод М-оценивания), впервые предложенный П. Хьюбером в 1964г [7].

Для того, чтобы как - то уменьшить нежелательную чувствительность критерия, основанного на (Y), вместо функции (Y; x), соответствующей исходной модели, используют ее ограниченную модификацию (Y; x) вида

(Y; x) =

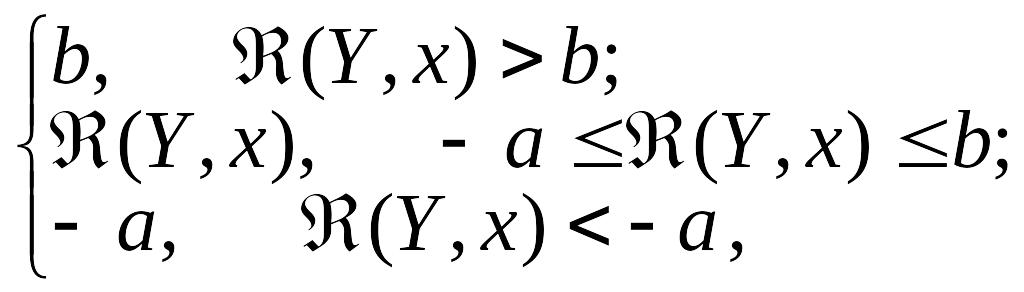
где a и b – постоянные.

При справедливости заданной модели и не слишком малых значениях a и b, эффективность критерия будет падать на краях области изменения x. Ограниченность (Y; x) влечет за собой нечувствительность (робастность) к влиянию небольшого числа ложных наблюдений. Изменяя длину интервала [– a, b], можно устанавливать компромисс между степенью робастности и снижением эффективности для принятой модели. Робастные методы оказываются полезными в тех случаях, когда при синтезе оптимальных процедур приходится учитывать возможность снижения их эффективности из - за отклонения характеристик входных данных от априорно предполагаемой модели. Робастные алгоритмы обработки сигналов обладают высокой эффективностью при номинальных условиях и приемлемой эффективностью в условиях, когда свойства сигналов и шума могут меняться в пределах заданных классов возможных характеристик.

Робастная процедура обработки сигнала для номинальной модели может уступать в эффективности процедуре, которая для этой модели оптимальна, но зато полная эффективность для данного класса моделей будет высокой или, по крайней мере, достаточной. При этом решение необходимо искать в виде процедуры, которая в наихудшем случае обладает оптимальной эффективностью, что приводит к минимаксным робастным алгоритмам.

Адаптивные алгоритмы сложнее минимаксных процедур фиксированной структуры, поэтому их целесообразно использовать в тех случаях, когда априорная неопределенность слишком велика (что не позволят обеспечить приемлемую эффективность минимаксных методов) или же имеются время или данные, необходимые для адаптации. Минимаксным АОЭИ отдают предпочтение в тех случаях, когда неопределенность классов имеет более ограниченный характер. Здесь их целесообразно использовать как робастные процедуры, предохраняющие от свойственного оптимальным методам чрезмерного падения эффективности при отклонении от исходных допущений. Минимаксные АОЭИ могут применяться и в рамках адаптивного подхода, поскольку механизм обучения в адаптивных процедурах никогда не предполагается настолько совершенным, чтобы за имеющееся ограниченное время произошла полная адаптация.

Для формализации робастного подхода при оценивании экспериментальных данных рассмотрим модель наблюдений

Y(t) = X(t) + N(t), –  < t < ,

где X(t), N(t) – сигнал и шум (действительные, центрированные, ортогональные, стационарные в широком смысле случайные процессы). Пусть X(t) и N(t) имеют соответственно спектральные плотности мощности Ф_X и Ф_N. Задача оценивания экспериментальных данных (фильтрации, предсказания или сглаживания) сводится к получению оценки X(t) по заданному процессу наблюдений Y(t) в форме

= ,

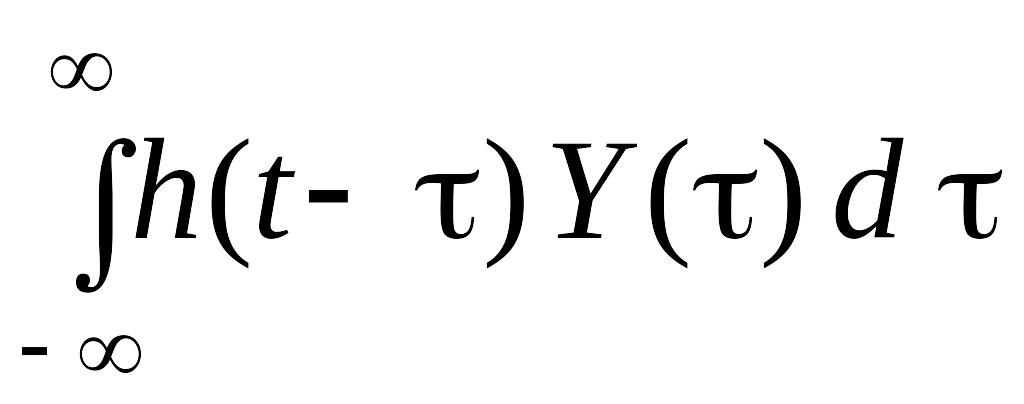где h – импульсная характеристика стационарного линейного фильтра. Качество полученной оценки сигнала характеризуется величиной квадратичного риска, который определяется выражением

E{ =

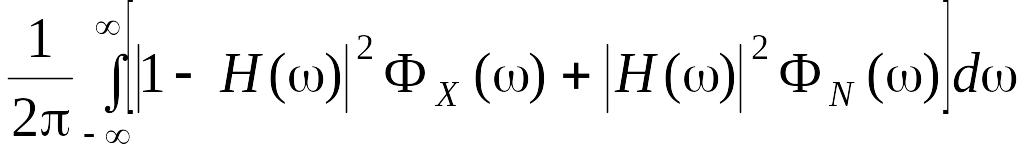= =e(Ф_X, Ф_N; H),

где H – передаточная функция, соответствующая h.

Робастный подход основан на минимизации по H величины падения эффективности фильтра, в наихудшем случае, по критерию:

.

Фильтр, удовлетворяющий данному критерию, является робастным по отношению к классам неопределенности  и .

Для решения этой задачи ищется седловая точка минимаксной игры, т.е. спектральная пара (Ф_X,L, Ф_N,L)   и фильтр H_R, удовлетворяющие условию

= = .

Согласно правому равенству, H_R является оптимальным фильтром для (Ф_S,L, Ф_N,L), то есть

H_R() = Ф_X,L()/(Ф_X,L() + Ф_N,L()).

Таким образом, определение седловой точки включает в себя отыскание пары (Ф_X,L, Ф_N,L), удовлетворяющей данному выражению. Левое равенство показывает, что фильтр H_R достигает наихудшей эффективности на спектральной паре (Ф_X,L, Ф_N,L), для которой он оптимален. Это наихудшее значение e(Ф_X,L, Ф_N,L, H_R) определяет гарантированный уровень эффективности фильтра H_R на классах  и . Так, если оба класса  и  порождаются всеми спектрами, которые отличаются от исходного не более чем на заданную величину , то робастный фильтр имеет вид

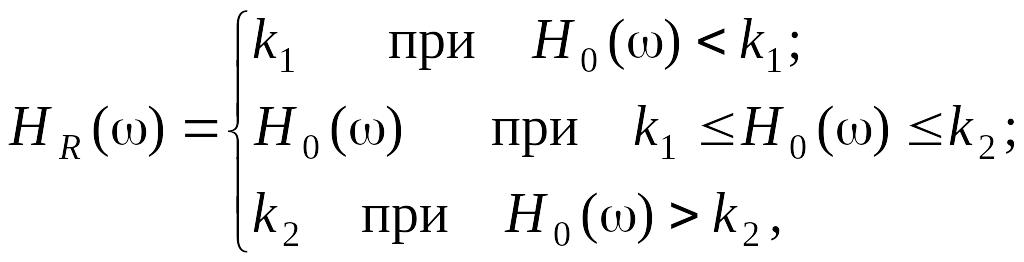
где H₀ = Ф_S/(Ф_S+Ф_N) – исходный фильтр, а константы k₁ и k₂ определяются значением  и конкретным типом использованной модели.

Соответствующее минимальное значение квадратичного риска определяется по формуле

e(Ф_X, Ф_N; H_W) = 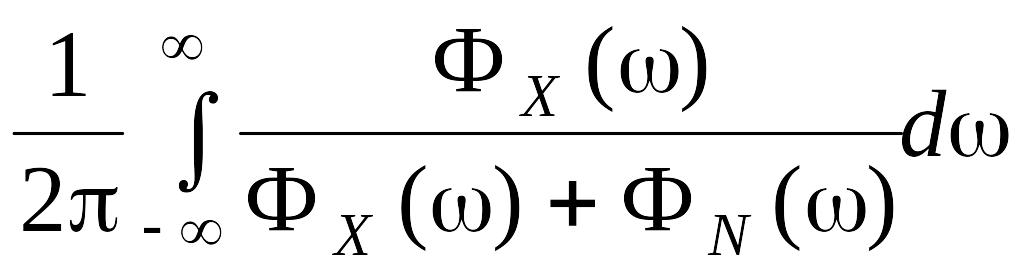= e_W(Ф_X, Ф_N).

Из полученного выражения следует, что для определения структуры алгоритма обработки информации необходимо знание спектра оцениваемого сигнала Ф_X() и шума Ф_N(), сопровождающего его измерение. Однако при измерении эти составляющие сигнала получают в смеси и отделить их друг от друга затруднено.

2. Выбор алгоритма обработки экспериментальной информации. Одним из наиболее широко используемых в обработке сигналов алгоритмов является дискретный фильтр Калмана [53], основанный на линейной модели наблюдений:

Y_n = H_nX_n + V_n, n = 0, 1, ....,

где Y_n – вектор наблюдения размером r для каждого n; H_n – матрица наблюдений; X_n – вектор состояния размером n; V_n – шум наблюдений.

Оптимальные по критерию минимума среднего квадратичного риска оценки X_n и X_n+1 по наблюдениям Y₀, ..., Y_n определяются рекуррентно, в соответствии с известным алгоритмом калмановской фильтрации:

_n+1= F_{n n} + W_n,

где F_n – одношаговая переходная матрица состояний; W_n – шум состояния.

Из общей теории минимаксного подхода к задачам математической статистики известно, что конечно-выборочная дисперсия минимаксными свойствами не обладает, что определяет использование робастных алгоритмов.

Для завершения формулирования требований к синтезируемому АОЭИ учтем, что процесс вычислений необходимо организовать таким образом, чтобы результат можно было не получать каждый раз заново, а только корректировать с учетом очередного поступившего результата измерения. Поэтому целесообразно использовать алгоритмы, в которых вычислитель, перед проведением любого информационного вычисления, располагает информацией о результатах всех предшествующих вычислений, достаточной памятью для хранения этих результатов и достаточным временем для их обработки, т.е. для проведения соответствующего алгоритмического вычисления необходимо использовать не пассивные (неадаптивные), а последовательные (адаптивные) алгоритмы. В данной ситуации радикальным решением является создание процедур с конечной памятью (на скользящем окне). В связи с этим целесообразно использовать рекуррентный метод вычисления в рамках критерия наименьших квадратов на окне, совпадающем с интервалом усреднения результатов измерения и перемещающемся по оси времени в виде “скользящего окна”. Сформулированным требованиям соответствует алгоритм, определенный по эволюционной теореме [53], для вычисления выборочного среднего с конечной памятью на “скользящем окне”, причем в рассматриваемом алгоритме используются усредненные весовые коэффициенты, с учетом всех значений, входящих в рассматриваемое “окно”.

В данном алгоритме в процессе адаптации определяется “окно” усреднения, а поскольку спектр оцениваемого сигнала неизвестен, то используется рекуррентный метод вычисления. Критерием качества результата решения является минимизация среднего риска вычисления на окне, совпадающем с интервалом усреднения результатов измерения и перемещающемся по оси времени при поступлении очередного значения (“скользящее окно”).

Для уменьшения смещений оценки параметра диагностирования предложено, в рамках метода, использовать усредненные весовые коэффициенты с учетом всех значений, входящих в рассматриваемое окно. Алгоритм, основанный на данном методе, состоит из следующих операций:

1. Начальной оценки по критерию минимума эмпирического риска [1], представляющую собой выборочное среднее:

.

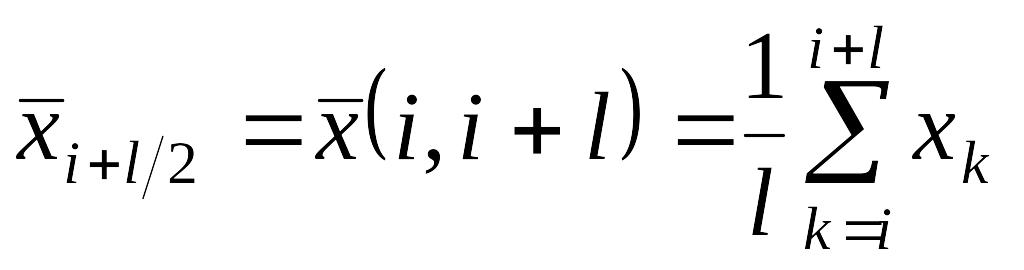2. Определения весового коэффициента предыдущего измерения:

.

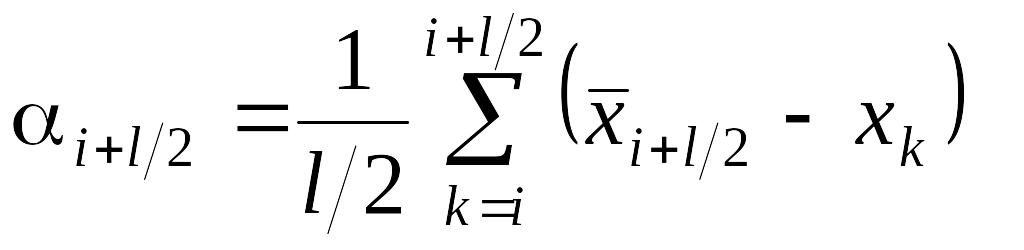3. Определения весового коэффициента последующего измерения:

.

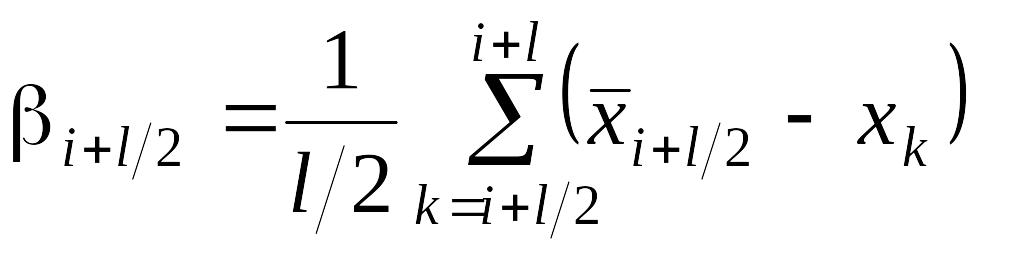4. Определения коэффициента передачи для нового измерения, на основании усреднения текущих и предыдущих весовых коэффициентов:

.

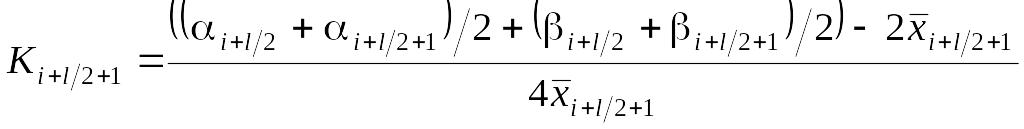5. Нахождения оценки нового измерения, получаемой согласно эволюционной теоремы [74]:

.

6. Принимая во внимание, что погрешности представляют собой некоррелированные случайные величины с нулевым средним и постоянной дисперсией , определяется величина текущего окна, при которой величина эмпирического риска [1, 89, 78] равна

.

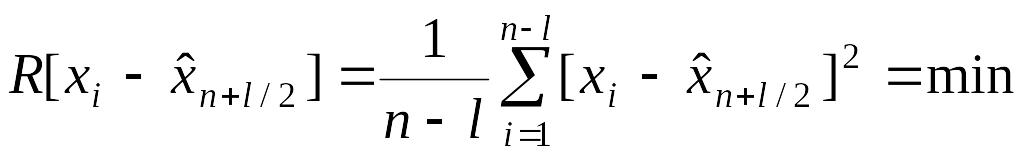Разработанный алгоритм реализован в виде программы для обработки осциллограмм, полученных при диагностировании зоны повреждения силовых КЛ (“ORSK”) [110]. Робастный АОЭИ для обработки осциллограммы диагностирования зоны повреждения силовой КЛ, синтезированный в разд. 6.5, реализован в программе "ORSK"V 2.0. Так, для кабеля СБ-325мм2 на напряжение 6кВ, длиной L_кл=300м, зона поражения которого произошла на расстоянии L_п=100м, получены результаты, представленные на рис. 3.4. При этом получены несмещенные оценки измеряемой величины, что достигается за счет введения в АОЭИ [110] усредненных весовых коэффициентов  и , которые определяются через выборочное среднее, но на соответствующих интервалах “скользящего окна”.

Другим достоинством модифицированного АОЭИ является отсутствие ухода оценок по интервалам измерения, что приводит к более точному отсчету данных интервалов при ОМП. Необходимо отметить увеличение числа операций в модифицированном АОЭИ на скользящем окне, которое ограничивает его применение при оценке параметров измерения в реальном масштабе времени. Вторым ограничением, накладываемым самим АОЭИ, является необходимость использования нечетного количества замеров в рассматриваемых окнах усреднения, что требуется для исключения ухода получаемых оценок по оси времени. Несмотря на указанные недостатки, для обработки экспериментальных данных, полученных в процессе диагностирования зоны повреждения силовых КЛ, предпочтительно применение модифицированного АОЭИ.

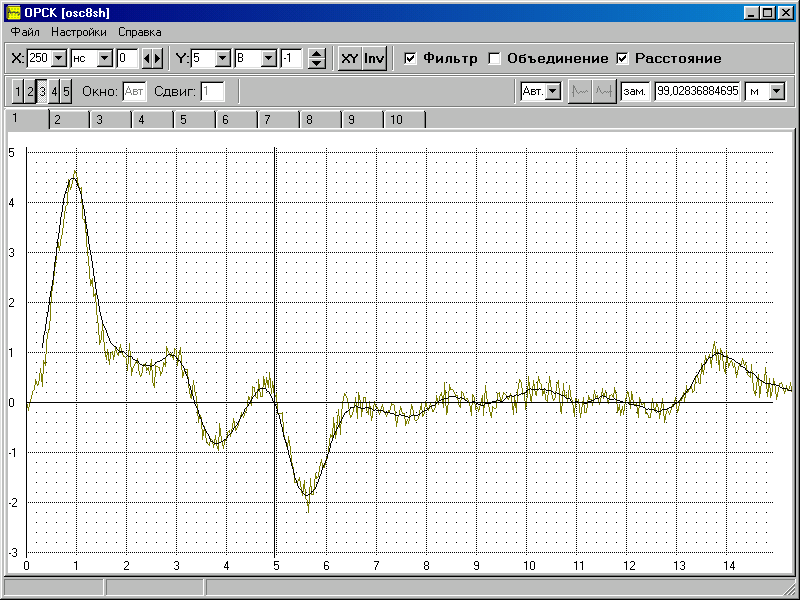
Рис. 3.4. Результаты обработки экспериментальных данных при определении расстояния до места повреждения силового кабеля модифицированным алгоритмом

Данная программа защищена свидетельством об официальной регистрации РОСПАТЕНТом [110].

Задача 3.2. Синтезировать алгоритм обработки экспериментальной информации, получаемой при исследовании акустических характеристик электротехнического оборудования.

Синтезированные в разд. 4.3, 4.4 АОЭИ, а также их робастный тип, полученный в разд. 6.5, можно использовать как при формировании высококачественной идентификационной модели (МИд) исследуемого объекта, так и при высококачественной оценке измеряемого параметра управляемого процесса, а для повышения качества экспериментальных данных на начальных этапах оценки целесообразно использовать алгоритмы, сформулированные выше.

Задача идентификации ЭСВМ включает постановку идентифицирующего эксперимента и решение задачи оценивания экспериментальных данных, полученных в эксперименте. При идентификации ЭСВМ эксперименты должны быть взаимосвязаны общей стратегией проведения. Для измерения параметров в автоматизированной системе научных исследований, контроля и испытаний при разработке и производстве элементов АСУ разработаны и внедрены алгоритмы обработки экспериментальной информации. Программная реализация данного алгоритма использована для автоматизации проектирования и наладки электроприводов корабельных вспомогательных механизмов в автоматизированной системе научных исследований на базе стенда. При этом контролировалась радиальная составляющая вибрационного ускорения ВИД в горизонтальной плоскости a_x. Для этого в верхнем углу вертикальной части основания стенда, к которой непосредственно крепится двигатель, был установлен датчик вибрации. Были получены осциллограммы вибрационного ускорения для различных значений тока питания фазы А при прямом и согласованном положении ротора, которые после обработки синтезированным алгоритмом приведены на рис. 3.5. На рис. 3.5 приведены результаты обработки осциллограмм вибраций для различных значений тока питания фазы А до и после обработки предлагаемыми алгоритмами. При этом линия 1 получена для разных значений риска.

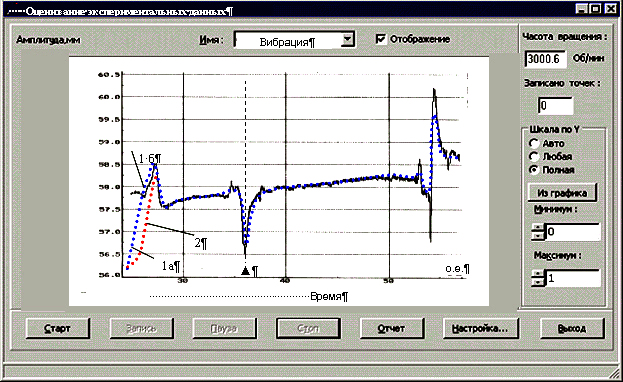
Рис. 3.5. Осциллограммы вибраций для различных значений тока питания фазы А до и после обработки предлагаемыми алгоритмами

На участке 1а риск АОЭИ выбран большим, чтобы быстро достигнуть значения оценки обрабатываемого процесса за счет снижения ее качества, а на участке 1б – равным риску кривой 2. В результате получаются оценки обрабатываемого процесса одинакового качества, но за разное время обработки, т.е. АОЭИ на участке 1 обладает большей эффективностью, что согласуется с выводом разд. 4.9. Синтезированные АОЭИ для исследования ЭСВМ обеспечили точность измерения параметра, не превышающую точность датчиков измерения –2–3%, что, следовательно, позволило более точно оценивать параметры МИд ЭСВМ.

Рис. 3.6. Пьезоэлектрический преобразователь виброизмерительный ДН–3–М1: 1 – основание; 2 – пьезоэлемент ЭП4К-1-3; 3 – винт; 4 – крышка; 5 – масса инерционная; 6 – втулка; 7 - контакт; 8 – втулка; 9 – колпачок; 10 – кольцо.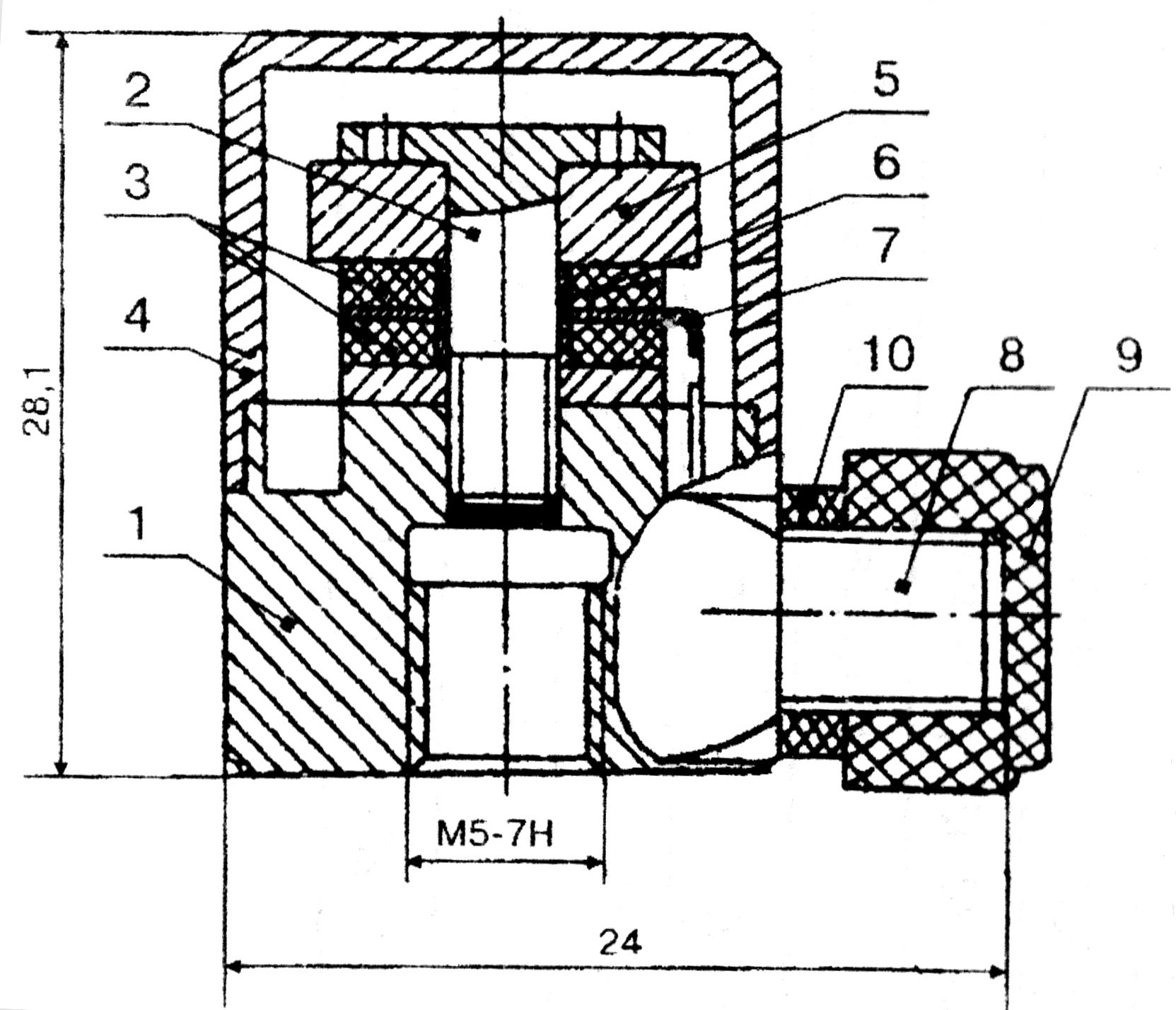

При решении задачи редукции необходимо задавать начальную импульсную переходную функцию первичного преобразователя, которая корректируется и уточняется на этапе идентификации обобщенного алгоритма оценивания. В качестве примера решения данной задачи рассмотрим ее частный случай.

Задача 3.3. Определить начальную импульсную переходную функцию виброизмерительного пьезоэлектрического преобразователя.

Решение задачи. На рис. 3.6 изображено устройство виброизмерительного пьезоэлектрического преобразователя ДН–3–М1 (паспорт 5Ф2.781.102 ПС), который используется в испытательном стенде для оценивания параметров ВИП. При воздействии механических колебаний на основание вибропреобразователя с ускорением а на инерционную массу m действует сила Р. Пьезоэлементы вибропреобразователя испытывают деформации сжатия – растяжения, в результате чего на грани пьезоэлементов, перпендикулярной вертикальной оси, возникают электрические заряды q, пропорциональные действующей силы P, с коэффициентом пропорциональности, равному индексу пьезомодуля а₁₁. Сигнал с кварцевых пластин снимается экранированным кабелем и поступает на измеритель шума и вибраций ВШВ – 003 – М3 (паспорт ИМ 2.745.000 ПС).

Эквивалентная схема преобразователя, соединенного кабелем с измерительной цепью, представлена на рис. 3.7. Произведем оценку параметров элементов данной схемы замещения. Так, собственное сопротивление пьезоэлемента R₀ определяется удельным сопротивлением материала пластин и их поверхностным сопротивлением.

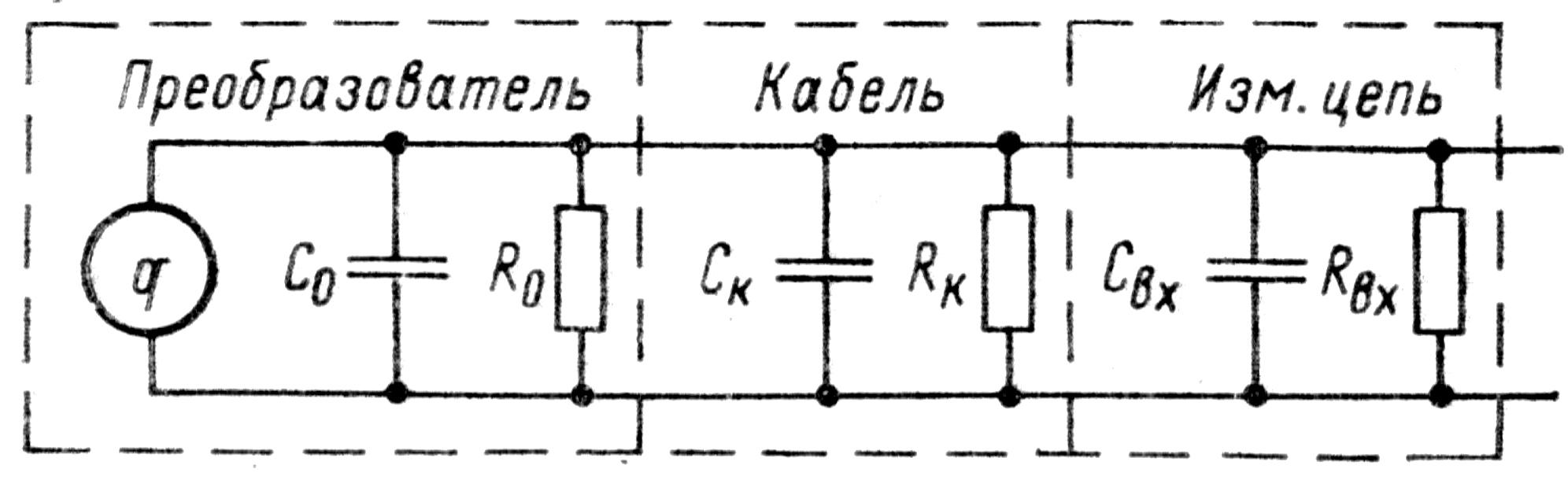
Рис. 3.7. Эквивалентная схема замещения пьезоэлектрического преобразователя: C₀ – емкость между гранями пьезоэлектрика (емкость преобразователя); С_к – емкость кабеля между жилой и экраном; С_вх – входная емкость измерительной цепи; R₀ – сопротивление преобразователя; R_к – сопротивление изоляции кабеля; R_вх – входное сопротивление измерительной цепи

Первая составляющая для кварца (10¹⁵ – 10¹⁶ Ом) значительно больше второй, поэтому определяющим является поверхностное сопротивление, для повышения которого до R = 10⁹  10¹⁰ Ом преобразователь приходится герметизировать, защищая его поверхность от влажности и загрязнения. Электрическое сопротивление изоляции используемого вибропреобразователя ДН–3–М1 и кабеля R_к при нормальных условиях применения не менее 10 ГОм (Под нормальными условиями применения принято: температура окружающего воздуха (205)С, относительная влажность от 30 до 80%, атмосферное давление от 84 до 196 кПа (от 630 до 795 мм рт. ст.)).

Наиболее высокое входное сопротивление R_вх (до 10¹³–10¹⁵ Ом) и входную емкость С_вх (до 20 пФ) измерителя шума и вибраций обеспечивают МДП – транзисторы, однако они имеют высокий уровень шумов. Поэтому для этих целей используют полевые транзисторы с p – n – переходом типа КП303Г, входное сопротивление которого составляет не менее 10¹¹Ом.

Используемый вибропреобразователь ДН–3–М1 имеет электрическую емкость при работе с кабелем длиной 2 м (C₀ + С_к) 1535325 пФ, а с кабелем 5 м 1800370 пФ. Анализируемую схему замещения можно привести к схеме, в которой включены параллельно сопротивление R и емкость С, где сопротивление R равно сопротивлению параллельного соединения R₀, R_к и R_вх, а емкость С = С₀ + С_к + С_вх. Данная схема замещения позволяет определить передаточную функцию пьезоэлектрического преобразователя с подключенной к нему измерительной цепью. Так, изменение силы P(t) создает переменный ток:

i = а₁₁dP(t)/dt,

где а₁₁ – индекс пьезомодуля для грани, перпендикулярной оси Х (вертикальной). Выходное напряжение преобразователя с подключенной к нему измерительной цепью составляет

_вых = ,

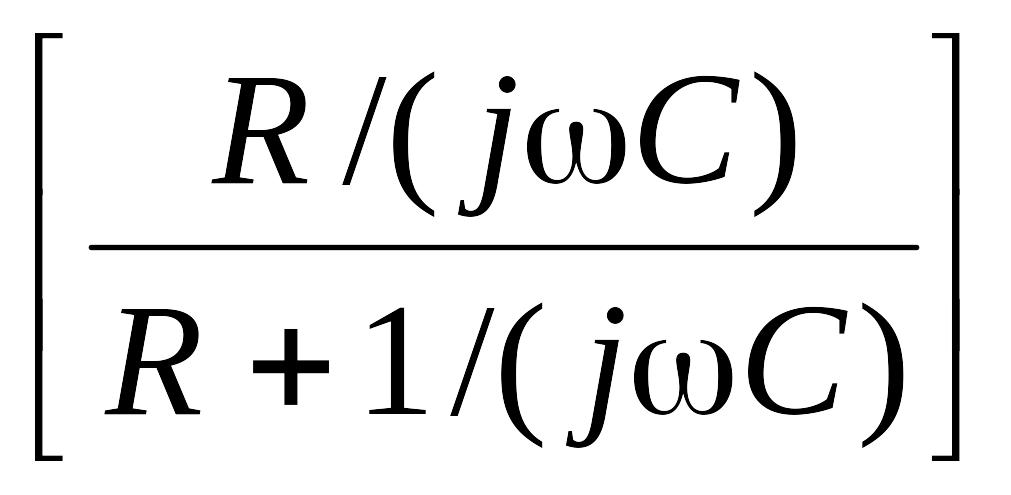где = ja₁₁ .

После простых преобразований получаем

_вых = а₁₁R .

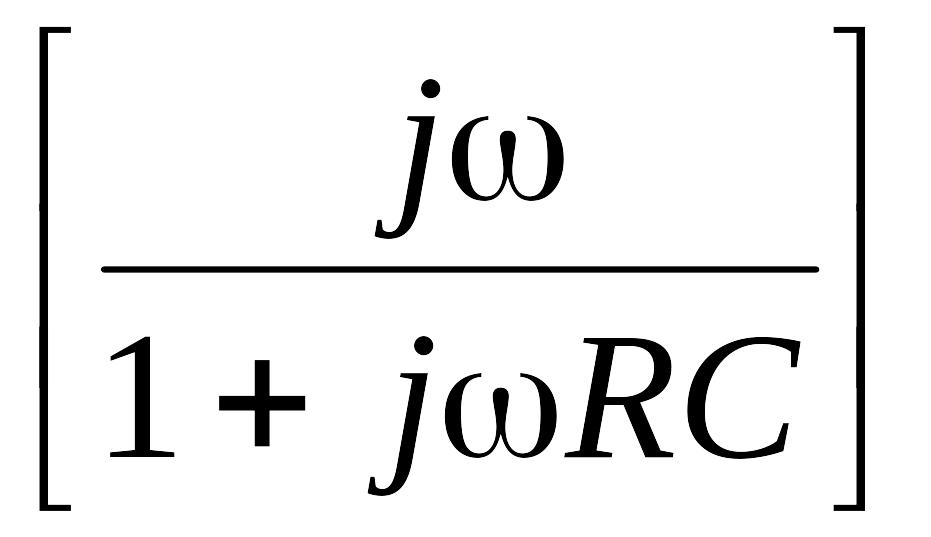Из данного выражения можно получить передаточную функцию виброизмерительного пьезоэлектрического преобразователя в виде

W_пэп(p) = ,

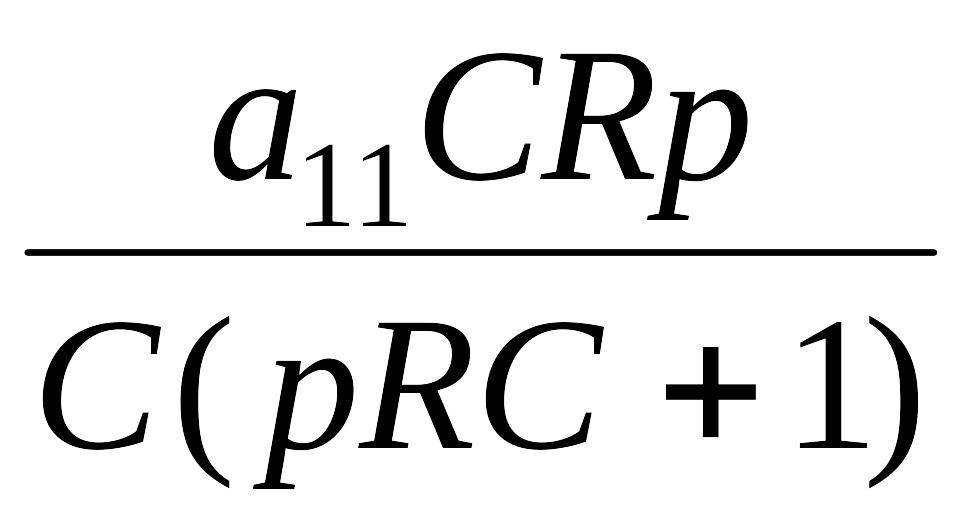которая соответствует передаточной функции неидеального дифференцирующего звена, переходная функция которого имеет вид [111]:

h_пэп(t) = ,

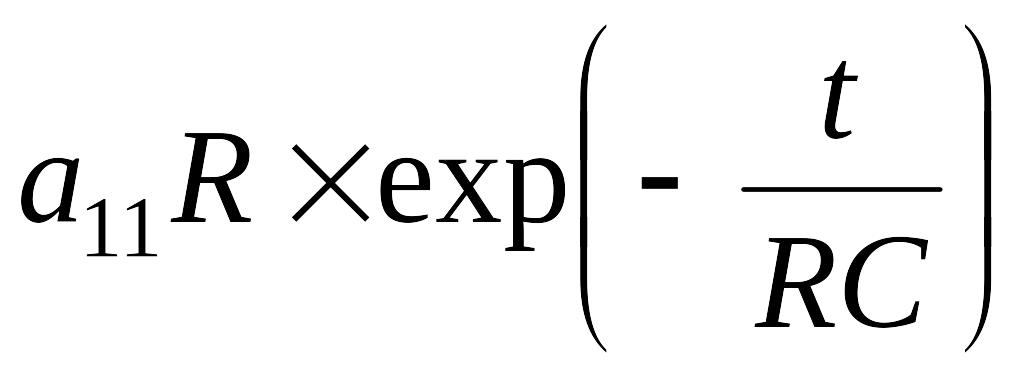а импульсная переходная функция –

k_пэп(t) = – .

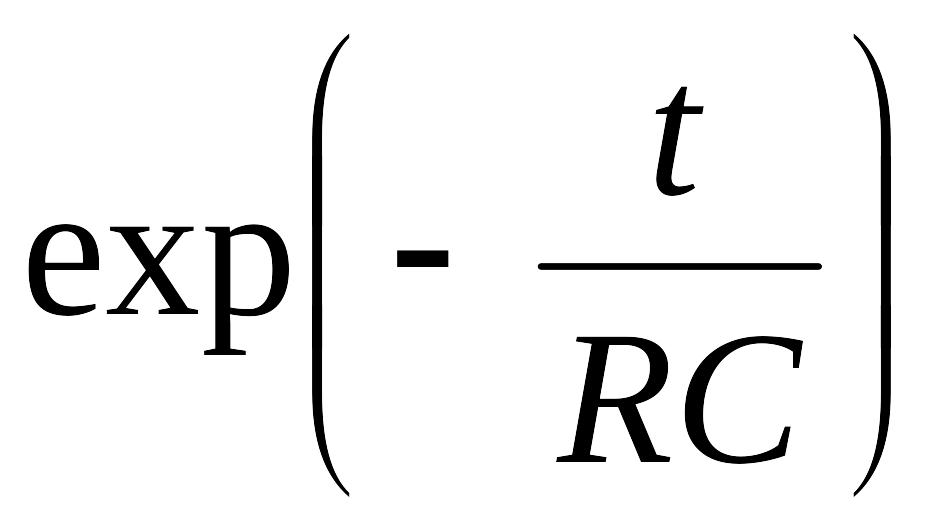Амплитудно-частотная характеристика преобразователя, включенного в измерительную цепь, имеет вид

H_пэп() = ,

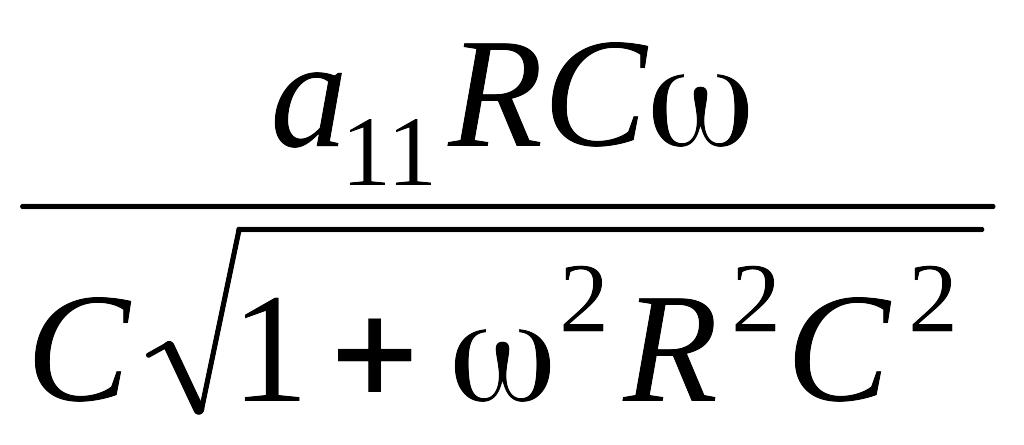а логарифмическая амплитудная характеристика –

20 lg H_пэп() = 20 lg + 20 lg RС– 20 lg .

Данная логарифмическая амплитудная характеристика аппроксимируется при < отрезком низкочастотной асимптоты вида

20 lg + 20 lg RC,

имеющей наклон 20 дб/дек, а при > – отрезком высокочастотной асимптоты – горизонтальной прямой 20 lg , пересекающейся с низкочастотной асимптотой при значении ₀ = . При этом фазо – частотную характеристику в области высоких частот можно представить в виде

 = arctg 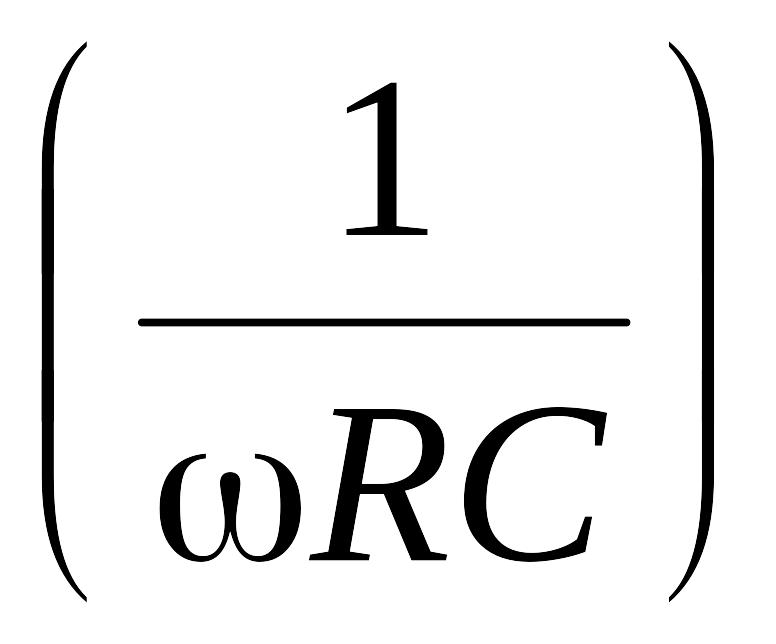= – RC.

Полученные характеристики позволяют определить выходной сигнал пьезоэлектрического преобразователя в виде

() = W() () = a₁₁Rexp[j( – RC)] (),

то есть выходной сигнал виброизмерительного пьезоэлектрического преобразователя ДН–3–М1 по величине пропорционален входному воздействию и сдвинут на соответствующую задержку.

Анализ полученной амплитудно-частотной характеристики показал, что для расширения частотного диапазона измеряемых величин в сторону низких частот (за счет сдвига точки ₀ = ) необходимо увеличивать постоянную времени T = RC. При этом расширение частотного диапазона путем увеличения емкости С осуществляется включением параллельно преобразователю конденсаторов, но из полученного выражения для амплитудно–частотной характеристики следует, что это уменьшает выходное напряжение преобразователя. Увеличение же сопротивления приводит к расширению частотного диапазона без потери чувствительности, однако это требует улучшения качества изоляции и применения усилителей с высокоомным входом.

Подводя итог проведенного исследования виброизмерительного пьезоэлектрического преобразователя ДН–3–М1, можно сделать вывод, что, несмотря на пропорциональность преобразования, данный тип датчика имеет достаточно большую временную задержку. Так, оценки параметров виброизмерительного пьезоэлектрического преобразователя ДН–3–М1 позволили определить постоянную времени RC < 1 с для датчика с усилителем напряжения. Для датчиков с усилителями заряда постоянные времени составляют 10 – 100 с. Однако уже при таких постоянных времени оказывается возможным проводить квазистатическую градуировку пьезоэлектрических датчиков.