3.5. Модификации алгоритма обработки экспериментальных данных

Первая модификация алгоритма. Рассмотренный в разделе 3.4 алгоритм можно путем модификации привести к алгоритму, рассмотренному в разделе 3.2. Для модификации простейшего алгоритма, вместо величины (N) на N-ом такте при задании длины шага S_N для общего выражения алгоритма (3.6), можно использовать изменение этих величин (N) – (N + 1) от шага к шагу, то есть градиент. Для того чтобы определить данную величину, преобразуем уравнение (3.6) к виду

= .

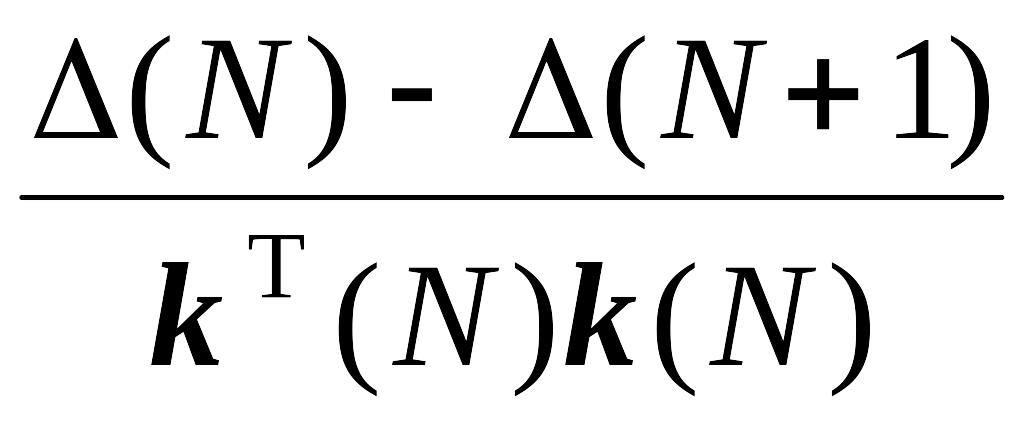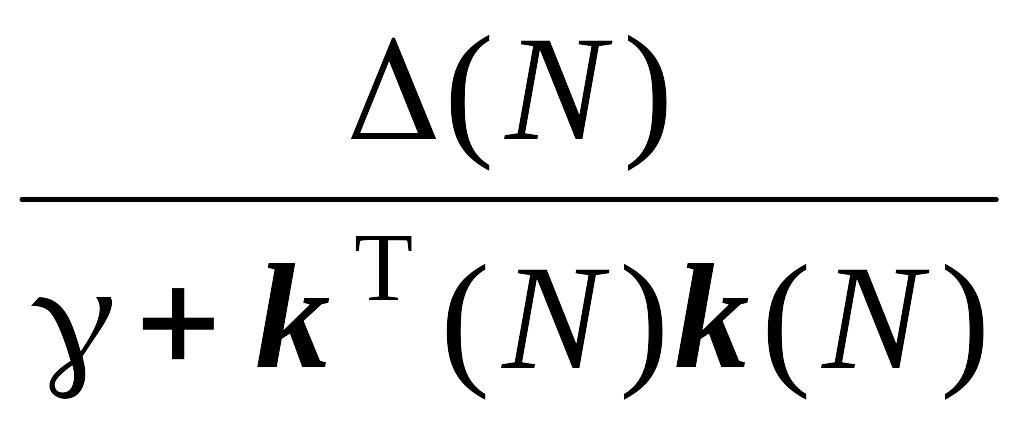Из данного уравнения следует, что если процесс описывается линейным уравнением (3.7), то для получения оценок параметров процесса на основании контроля выходов, можно использовать следующий алгоритм:

x_i(N)=

=x_i(N–1)+_i[y(N)– _i(N–1)x_i(N)][ _i²(N)]^–1k_i(N), (i = 1, 2,...,n), (3.16)

где x_i(N) – оценки параметров измеряемого процесса в N-м такте; _i – весовые коэффициенты (константы). Таким образом, модифицированный алгоритм полностью совпадает с алгоритмом, проанализированным в разделе 3.2.

В векторной форме этот же алгоритм может быть записан в виде

x(N) = x(N – 1) + Г[y(N) – k^T(N – 1)x(N)](k^T(N)k(N))^–1k(N), (3.17)

где Г = 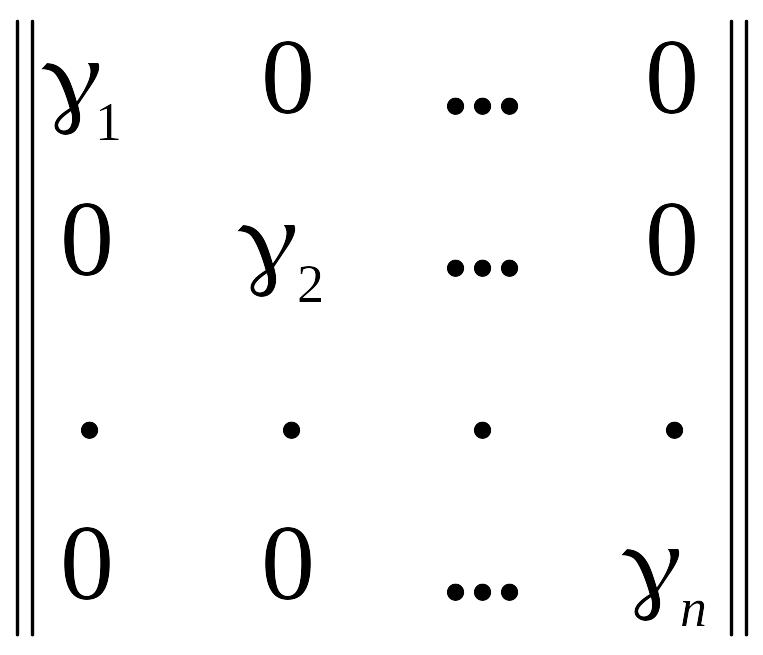– диагональная матрица.

Вторая модификация алгоритма. Целью дальнейшей модификации рассмотренного в разд. 3.4 алгоритма является увеличение его сходимости. Для анализа возможностей данного алгоритма воспользуемся введенным в разделе 3.4 вектором ошибки _x(N), и формулу (3.8) можно переписать в виде

_xi(N)=_xi(N–1)–_i[ _xi(N–1)k_i(N)][ _i²(N)]^–1k_i(N), (i = 1, 2,..., n). (3.18)

Возведя в квадрат обе части равенства (3.18) и упростив их, получим

_x^T(N)_x(N)= _x^T(N–1)_x(N–1){1–[_x^T(N–1)k(N)]²/[^T(N–1)

(N–1)k^T(N)k(N)]}.

В фигурных скобках данного уравнения, как и в уравнении (3. 4) для риска общего алгоритма оценки (3. 5), стоит квадрат синуса угла между векторами _x(N – 1) и k(N), то есть sin²(_x(N –1)k(N)). Таким образом, _x^T(N)_x(N) не больше, чем _x^T(N – 1)_x(N – 1), а сумма квадратов ошибок определения всех коэффициентов не может увеличиться ни при каком изменении воздействий на входе.

Чтобы в произвольном шаге произошло уменьшение ошибки (если она не равна нулю), достаточно, чтобы вектор входных воздействий x(N) не был параллелен предыдущему вектору входных воздействий x(N – 1). В этом случае синус не будет равен единице, и ошибка уменьшится, то есть в модифицированном алгоритме таким образом определяется оптимальное направление s_N поиска оценки результата измерения. В общем случае необходимо, чтобы во входном воздействии чередовались, по крайней мере, n линейно-независимых векторов, и наибольшее быстродействие одношаговый алгоритм (адаптивный) обеспечивает при подаче на входы объекта ортогональных векторов, что возможно только по управляемым входам при проведении активного эксперимента и невозможно по наблюдаемым каналам.

Рассмотренный алгоритм определяет параметры объекта при произвольных начальных условиях, причем сумма квадратов ошибок определения всех параметров монотонно уменьшается. При случайных входных векторах, алгоритм обеспечивает сходимость в среднем квадратическом. Каким бы ни был выбран вектор начальных оценок x(0), если корреляционная матрица входных переменных не вырождена, после достаточно большого количества итерации x(N) сколь угодно мало будет отличаться от вектора x.