3.3. Общий алгоритм оценки измеряемого параметра

Сформулированный в разд. 2.3 идентфикационно- редукционный метод оценивания, позволяет сформировать следующий АОЭИ при минимизации риска:

1. Имеются исходные экспериментальные данные, полученные в результате эксперимента по соответствующему плану _N0 = {x₁,..., x_N0}, для которого матрица M(_N0, ) выражена при всех . Полагаем j = 0.

2. Определяют на основании полученных данных оценку _i(y) в соответствии с соотношением (3.5).

3. Вычисляют оценки, удовлетворяющие минимуму эмпирического риска оценивания результатов измерения для выбранного плана эксперимента _Nj=Arg N_j^–1 –(x_i, ))², и для оценки определяют матрицу М(_Nj, _Nj)=N_j^–1 (x_i, _Nj)f^T(x_i, _Nj).

4. Отыскивается новая точка x_Nj+1 = Arg (x, _Nj, _{N j}), где

(x, , ) = f^T(x, ) f(x, ).

5. Определяется риск стратегии, включающий как стоимость С(x₁, x₂, ..., x_n), так и точность оценки параметра g_n(x₁, x₂, ..., x_n) по основному функциональному уравнению, определяющему бесконечную последовательность функций потерь g_n(x₁, x₂,..., x_N), которая задает соответствующий риск вида [40]:

R_n(x₁, x₂,.., x_N)=

= .

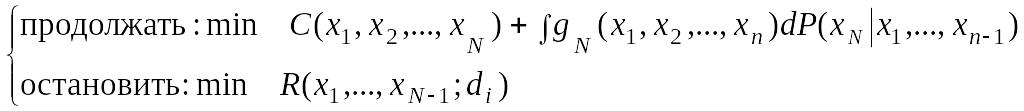6. В случае, если достигнута заданная точность оцениваемого параметра, то алгоритм завершается. В противном случае осуществляется постановка эксперимента в точке x_Nj+1 и получают наблюдение y(x_Nj+1); при этом

_Nj+1=[1–(N_j+1)^–1]_Nj+(N_j+1)^–1(x_Nj+1),

где N_j+1=N_j+1, заменяется j на j + 1 и переходят к пункту 3.

Данный алгоритм доставляет на каждом N – м шаге приближенно максимальное уточнение оценок _N (в смысле выбранного критерия ). Причем на каждом шаге может определяться несколько опорных точек x_N+1,..., x_N+q, повторяя п.п. 4 – 6 с одними и теми же значениями оценок _N. При этом в одной опорной точке проводятся серии наблюдений, длина которых близка к величине _sN/(1 – _s).

Таким образом, при минимизации риска и оценивании параметра x в методах локального поиска получается последовательность точек ₀, ₁,..., ( _i ), при некоторых предположениях сходящаяся к x, для которой риск минимален. Выбор способа построения этой последовательности и минимизация риска зависит от свойств функции f, от информации, которая используется на каждой итерации и от технических средств, которыми располагает исследователь для реализации вычислительных методов. Даже при сравнительно небольшом количестве “избыточных” данных, эффективность найденных правил решения близка к эффективности соответствующих оптимальных байесовых правил, а при увеличении объема полной совокупности данных наблюдения y происходит достаточно быстрая сходимость к результатам, которые имели бы место при отсутствии априорной неопределенности. Общая блок - схема программы формирования оценки, в соответствии с предложенным методом, приведена на рис. 3.1. На структурном этапе формирования оценки в предлагаемом методе синтезируется структура ММИ. Для этого, в соответствии с главой 3, на основании полученных исходных экспериментальных данных, осуществляется выбор количества переменных в исходной ММИ, обеспечивающих предельное значение пропускной способности эксперимента, в котором получены используемые данные.

В соответствии с разд. 3.3 (при последовательном накоплении экспериментальных данных) вычисляются области определения переменных ММИ и риск выбора каждой компоненты ММИ, а в соответствии с разд. 3.6 осуществляется вычисление разделяющей функции между переменными ММИ. Первая итерация алгоритма формирования ММИ является априорной и включает [82]: разбиение признаков на классы (составление априорного алфавита классов); определение наилучших границ классов в априорном признаковом пространстве; выбор алгоритма распознавания, который определяет рабочий алфавит классов и их границы.

При решении сформулированной задачи формирования ММИ целесообразно использовать датчик, важной особенностью которой является возможность обучаться. Формирование ММИ в этом случае сводится к процессу обучения и осуществляется по простым, хорошо отработанным алгоритмам. При этом решаются задачи управления проведением физических экспериментов, задачи распознавания и классификации образов, выявления закономерностей в разных предметных областях.

При обучении осуществляется выработка в обучаемом датчике той или иной реакции на группы внешних идентичных сигналов путем многократного воздействия на датчик внешней корректировки в виде “поощрений” и “наказаний”. Механизм генерации этой корректировки практически полностью определяет алгоритм обучения. Самообучение отличается от обучения тем, что здесь дополнительная информация о верности реакции датчика не сообщается.

Ввод данных контроля для

обучающей выборки

Выбор из них данных и

признаков для анализа на основании пропускной способности модели

Вычисление разделяющей функции

Вычисление интервальных оценок

Определение риска оценки R_di

Вывод

оценки

D = R_di – R_di–1

Определение риска модели контроля R_Mi

>0 (>e) =0 (=e)

D

M = R_Mi – R_Mi–1

Постановка

дискриминирующего

эксперимента

>0 (>d)

M

=0 (=d)

Постановка

отсеивающего

эксперимента

Объединение новых

данных и

обучающей выборки

Рис. 3.1. Общая схема алгоритма формирования оценки

Причем результат самообучения характеризует пригодность выбранного пространства для конкретной задачи обучения распознаванию. Если абстрактные образы, выделяемые в процессе самообучения, совпадают с реальными, то пространство выбрано удачно. Чем сильнее абстрактные образы отличаются от реальных, тем “неудобнее” выбранное пространство для конкретной задачи.

При адаптации осуществляется изменение параметров и структуры датчика, а возможно и управляющих воздействий на основе текущей информации, с целью достижения определенного состояния датчика при начальной неопределенности и изменяющихся условиях эксперимента для получения требуемого качества оценивания результатов измерения. При этом осуществляется обучение, в результате которого датчик постепенно приобретает способность отвечать нужными реакциями на определенные совокупности внешних воздействий.

На параметрическом этапе формирования ММИ, на основании полученных исходных данных измерения, осуществляется, в соответствии с разд. 3.10, определение параметров исходной ММИ с заданным риском. Полученная ММИ позволяет осуществлять постановку дискриминирующего эксперимента, по результатам которого уточняется первичная модель. После этого на базе полученной первичной дискриминированной модели, ставится отсеивающий эксперимент, по результатам которого осуществляется формирование “отсеянной” модели, которая обеспечивает минимизацию в ней количества значимых факторов.

Общая модель адаптивной стратегии статистического оценивания результатов измерения сводится к последовательности одинаковых статистических задач оценивания с измеримым пространством решений ( , D), определяемых в соответствии с последовательностью статистических экспериментов, в каждом из которых истинное значение x трактуется как реализация случайной величины  с некоторым априорно фиксированным распределением G на (_x, В). При этом адаптивная стратегия характеризуется решением об остановки эксперимента s₀ и решением о его продолжении s₁. Относительно распределения G известно только, что оно принадлежит некоторому классу априорных распределений G. Если (x) – априорная плотность параметра x по мере  на (_x,В), то можно ввести образ правила _d, как (Dx) = M_x(Dy^(v)), и его безусловный образ (D) = M^(D) с плотностями распределения (x) и () соответственно. Величина средних потерь при апостериорном подходе определяется как условное математическое ожидание функции потерь L(, ) относительно решающей функции  = _n(Y⁽ⁿ⁾) [8], то есть апостериорный риск при стратегии оценивания Ф = <_s, _d> равен

R() = R(Ф) = E{L(,)} = ,   D,

где (x) = (x) (x)/(), если () > 0 и (x) = 0 при () = 0.