Типовые задачи и примеры их решения

Задача 2.1. Определить риск замены случайной величины х случайной величиной y (согласно выражения 1.1), выборочным пространством  для которых является евклидовое пространство R² двух измерений с элементами Х= (х, y).

Решение задачи. Для решения задачи примем гипотезу H₁, по которой x и y – зависимые переменные с совместной плотностью распределения f(x, y), и гипотезу H₂, по которой x и y – независимые переменные с соответствующими плотностями распределений g(x) и h(y). Тогда значение средней информации в y относительно x можно определить как

I(y:x) = . (2.21)

В частности, если H₁ задает двумерное нормальное распределение с плотностью

f(x, y) = ,

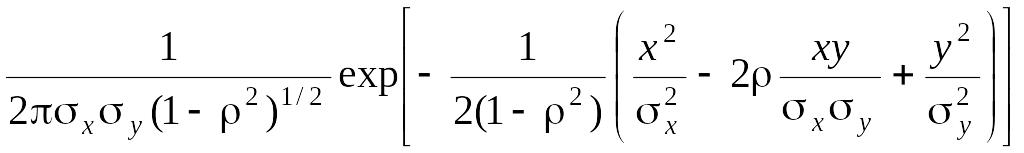а H₂ – произведение частных нормальных плотностей распределения

g(x) = 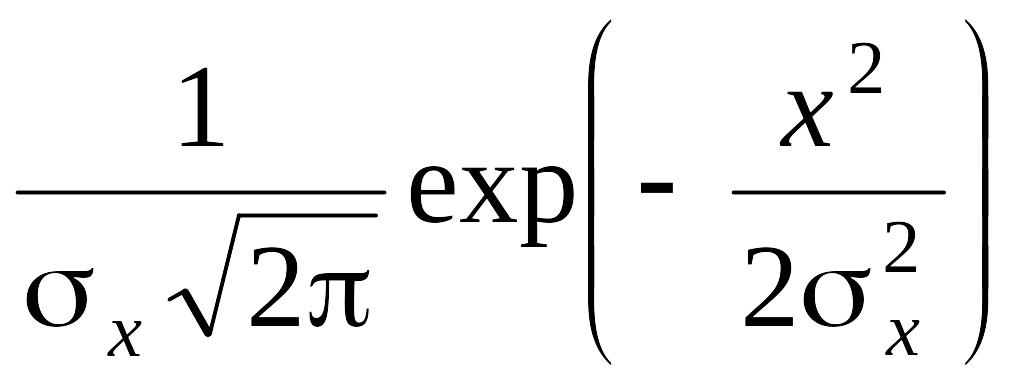h(y) = ,

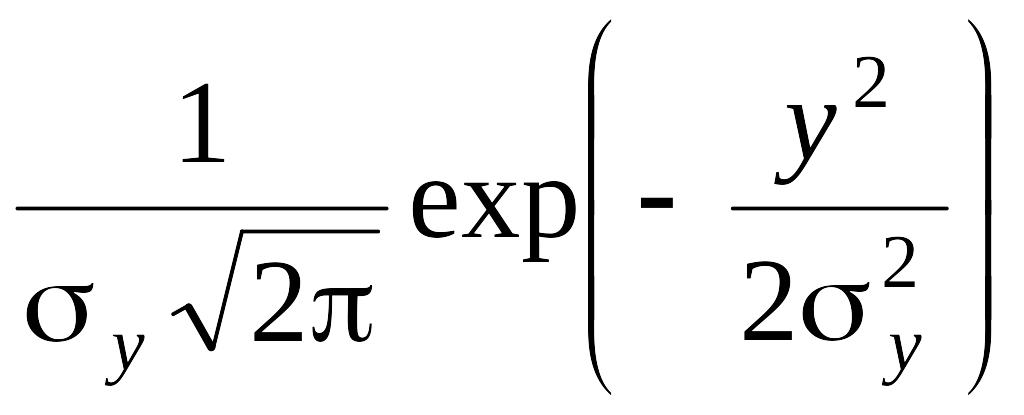то находим

R(x,y)= – = =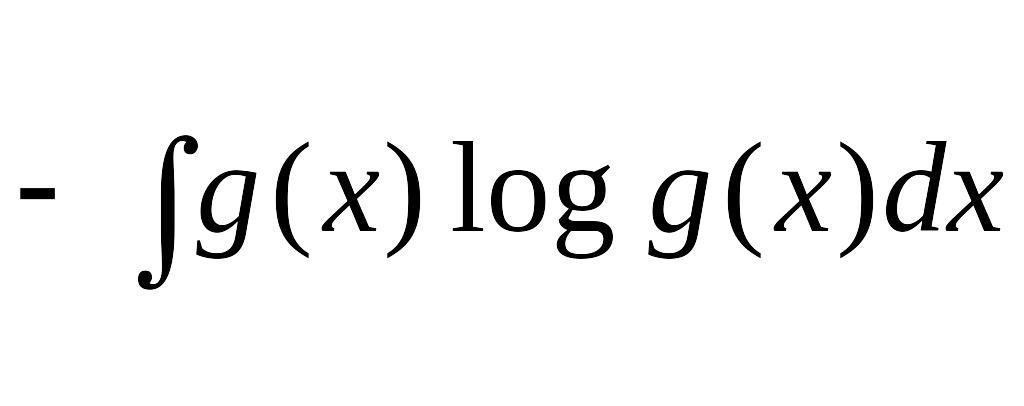

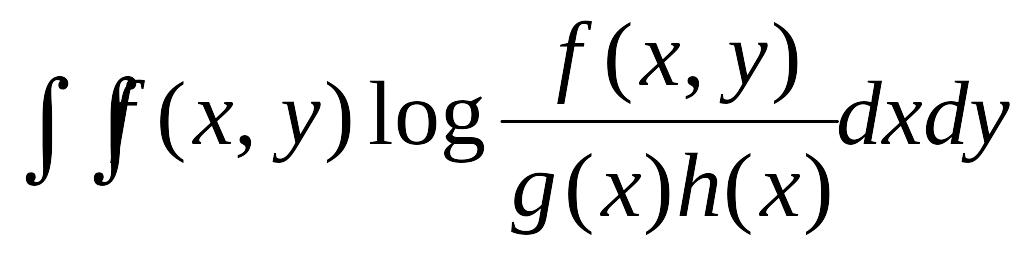= (2.22)

так что R(x, y) является функцией коэффициента корреляции r и изменяется от 0 до ¥, когда изменяется от 0 до 1.

Задача 2.2. Определить приведенный риск передачи сигнала в системе связи на фоне аддитивного шума, обеспечивающий наибольшую информативность (энтропию) при одинаковой мощности излучения.

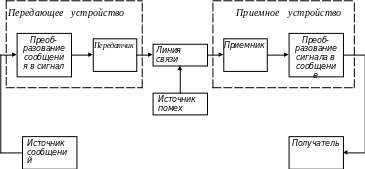
Описание предметной области. Системой связи называется совокупность технических средств для передачи сообщений от источника к потребителю [Теория передачи сигналов: Учебник для вузов/ А. Г. Зюко, Д. Д. Кловский, М. В. Назаров, Л. М. Финк. – М.: Радио и связь. – 1986. – 304с.]. Структура данной системы приведена на рис. 2.4. Этими средствами являются передающее устройство, линия связи и приемное устройство.

Основы современной теории связи заложены в важных статьях Найквиста [Nyquist H., “Certain Factors Affecting Telegraph Speed”, Bell System Technical Journal, April 1924, p. 324; “Certain Topics in Telegraph Transmission Theory”, A.I.E.E. Trans., v. 47, April 1928, p. 617.] и Хартли [Hartley R. V. L., “Transmission of Information” Bell System Technical Journal, July 1928, p. 535.]. Основной задачей связи является восстановление (точное или приближенное) в данной точке сигнала, отправленного в другой. Часто сигнал имеет некое значение, то есть соотносится или коррелирует с заданными состояниями некоторой системы. Однако эти семантические аспекты связи не имеют отношения к инженерной задаче, важно лишь то, что сообщение выбирается из некоторого набора возможных. Система связи должна одинаково хорошо работать со всеми возможными вариантами сообщения, а не только с тем, который будет выбран в действительности – на этапе разработки системы это еще неизвестно.

Рис. 2.4. Структурная схема системы связи

Рассмотрим назначение отдельных элементов этой схемы и проиллюстрируем происходящие в них процессы.

Источник сообщения, создающий сообщение или серию сообщений для связи с приемной станцией. Сообщения могут быть различных типов: а) последовательностью букв, как в телеграфной системе; б) некоторой функцией времени f(t), как в системе телефонной связи; в) функцией времени и других переменных, как в телевизионных системах – такое сообщение можно рассматривать как функцию f(x, y, t) двух пространственных координат и времени, представляющую интенсивность излучения в точке (x, y) в момент времени t на фотокатоде; г) двумя или более функциями времени, к примеру f(x), f(y), f(t), как в случае передачи “трехмерного звука” или просто нескольких сигналов одновременно; д) несколькими функциями нескольких переменных – при передаче цветного телевизионного сигнала мы имеем дело с тремя функциями, f(x, y, t), q(x, y, t), h(x, y, t) определенными на трехмерном множестве (можно рассматривать три этих функции также, как компоненты трехмерного векторного поля в пространстве); кроме того, различные виды сигналов могут возникать при передаче телевизионного изображения совместно со звуком каналом.

Передающее устройство, преобразующее неким образом сигнал и делающее его пригодным для передачи по линии связи. В телефонии это сводится главным образом к преобразованию давления звука в пропорциональный электрический сигнал. В случае телеграфа процесс кодирования сигнала преобразует его в последовательность точек, тире и пробелов в линии связи. В многоканальной PCM-системе различные функции различных голосов должны быть дискретизованы, сжаты, закодированы и, наконец, сведены надлежащим образом в один сигнал. Вокодеры (устройства цифрового кодирования речи), телевидение и частотная модуляция – другие примеры сложных преобразований, которым может быть подвергнуто сообщение при формировании сигнала.

Линия связи, представляющая собой среду, используемую для передачи сигнала от передатчика к приемнику. Это может быть парой проводов, коаксиальным кабелем, радиоволнами определенной частоты, лучом света и т.д.

Приемное устройство, выполняющее задачи, противоположные выполняемым передатчиком, а именно – восстановления сообщения из сигнала.

Получатель – человек (или устройство), для которого сообщение предназначено.

В устройстве преобразования сообщения в сигнал непрерывное сообщение, поступающее с выхода источника, преобразуется в форму для передачи. Проходя через линию связи, сигнал подвергается воздействию различного рода помех, и на вход приемника поступает смесь полезного сигнала и помехи. Приемник обрабатывает эту смесь и принимает решение о том, какой сигнал передавался. С выхода приемника сигнал поступает на устройство преобразования сигнала в сообщение и к получателю приходит сообщение, подобное сообщению на выходе источника.

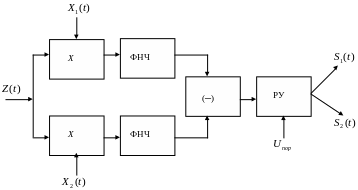
На вход приемника поступает смесь сигнала и помехи Z(t) (рис. 2.5).

Суть когерентного метода приема заключается в том, что на приемной стороне о передаваемом сигнале известно все: частота, фаза, длительность, момент прихода. Поэтому, сигналы Х₁(t) и Х₂(t) – точные копии передаваемых сигналов. Устройства умножения эти копии перемножаются с Z(t). Далее произведения Х₁(t)Z(t) и Х₂(t)Z(t) проходят через ФНЧ, вычитаются в вычитающем устройстве и поступают на вход решающего устройства, где происходит сравнение с пороговым напряжением. Решение принимается в пользу того сигнала, у которого функция взаимной корреляции будет больше.

Ниже рассмотрены некоторые общие задачи, имеющие отношение к системам связи. При этом различные вышеупомянутые элементы представляются математическими величинами, отвлекаясь от их физической сущности.

Рис. 2.5. Структурная схема приемника

Решение. Предположим, что x является переданным сигнальным напряжением, а y – полученным сигнальным напряжением, состоящим из передаваемого сигнального напряжения и аддитивного шума, т.е. y = x +n, где n – шумовое напряжение. Шум и передаваемый сигнал можно считать независимыми, так что

f(x, y) = g(x) h(y|x) = g(x) h(y – x). (2.23)

Риск R(x, y) в соответствии с равенством (2.21) является мерой связи между полученным и переданным сигналами и является в таком случае характеристическим свойством канала связи. В соответствии с экстремальным свойством для нормального закона распределения [96] получаем

f(x,y)=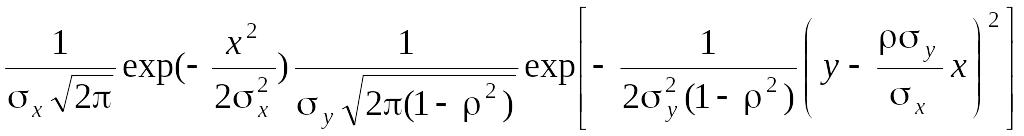 ,(2.24)

то сравнивая (2.24) и (2.23) видим, что h(y|x) = h(y – x), если

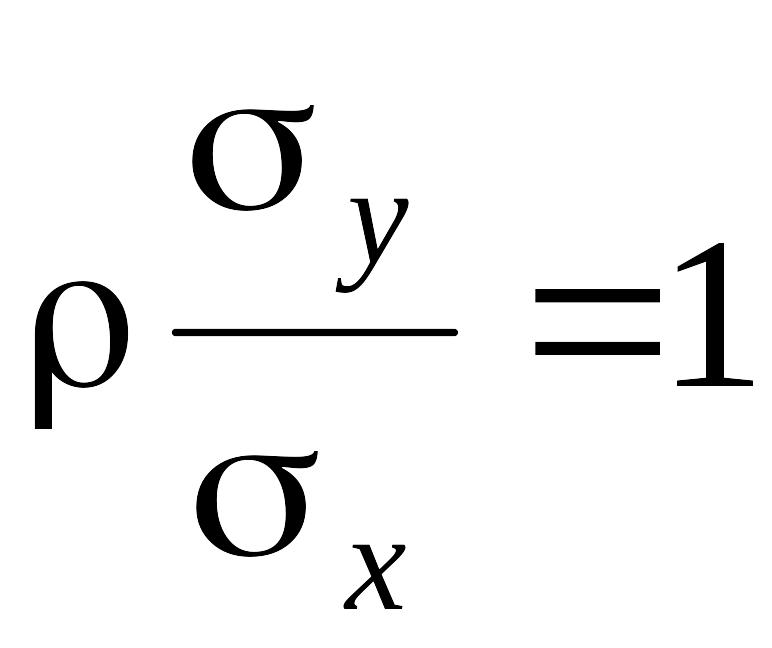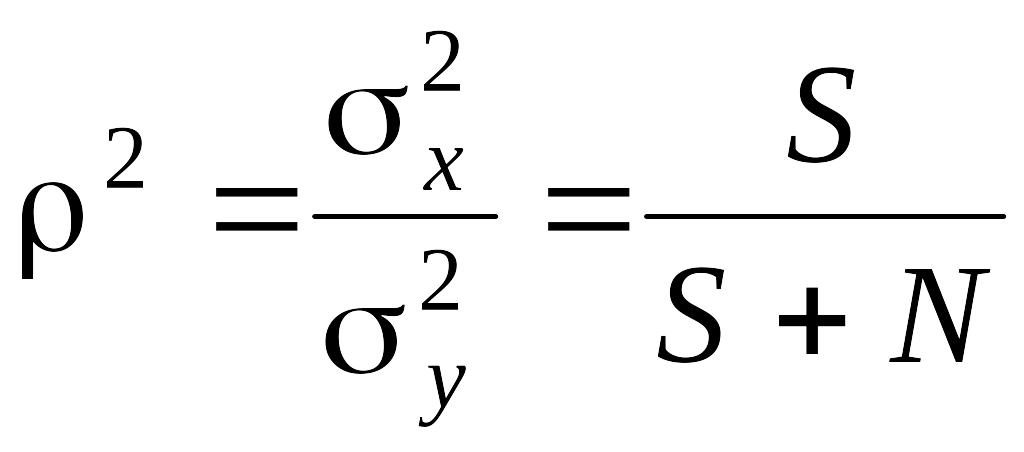, , (2.25)

где S = E(x²) – средняя мощность передаваемого сигнала, N = E(n²) – мощность шума. Подставляя величину r² из равенства (2.25) в (2.22) и (2.23), найдем, что потери средней информации в полученном сигнале относительно переданного равны, т.е. приведенный риск

R(x, y) = ,

где k_шс = – коэффициент шум / сигнал.

Задача 2.3. Определить риск выделения переменных модели измерения, обеспечивающих наибольшую энтропию среди всех распределений с одним и тем же ограниченным интервалом возможных значений непрерывной случайной величины.

Решение. Требование обеспечения наибольшей энтропии при выделении переменных модели измерения определяет то, что при измерении искомые подобласти, формируемые в процессе измерения по искомой модели измерения и соответствующие гипотезам H₁ и H₂, характеризуются равномерным законом распределения и в общем случае определяются на интервалах 0 £ x £q₁, 0 £ x £ q₂, q₁ < q₂, причем q₁ < q₂ и

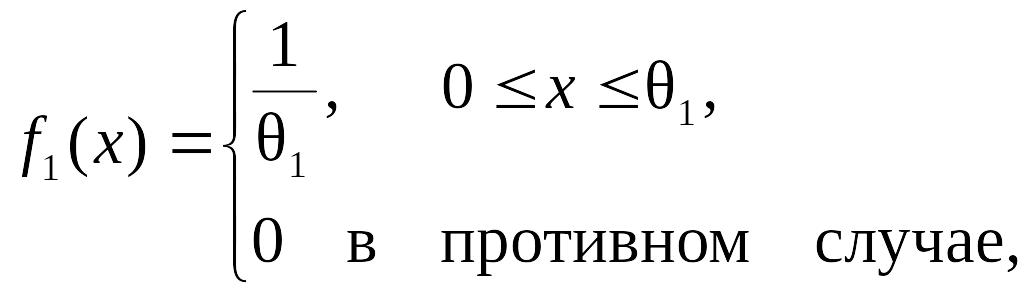
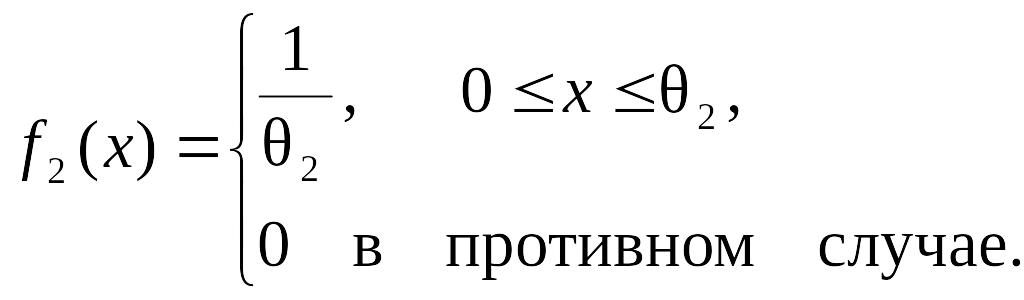
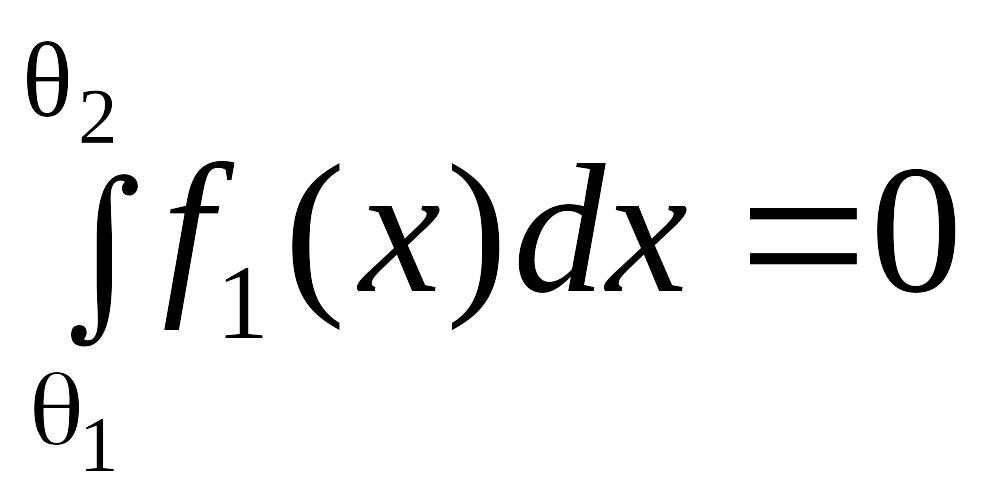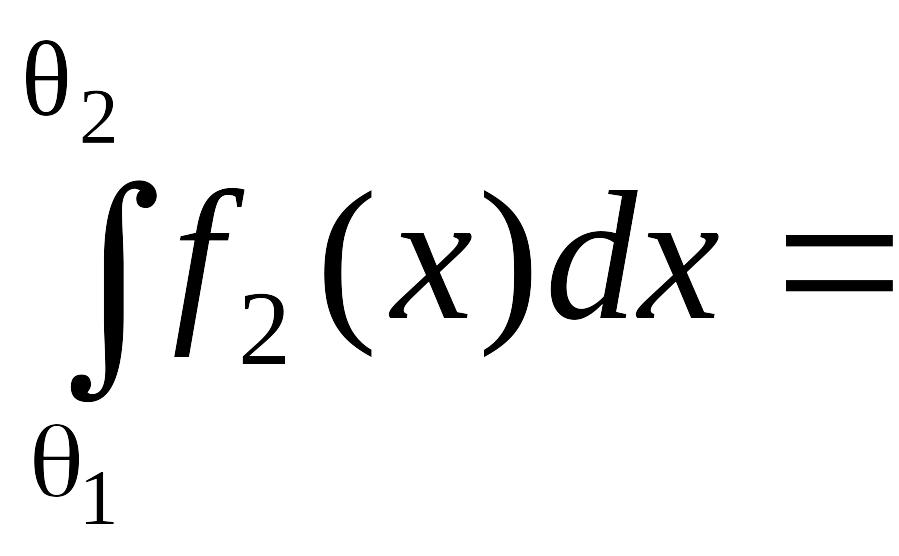
Поскольку для интервала E = {x: q₁ £ x £ q₂} вероятность m₁(E) = , а m₂(E) = 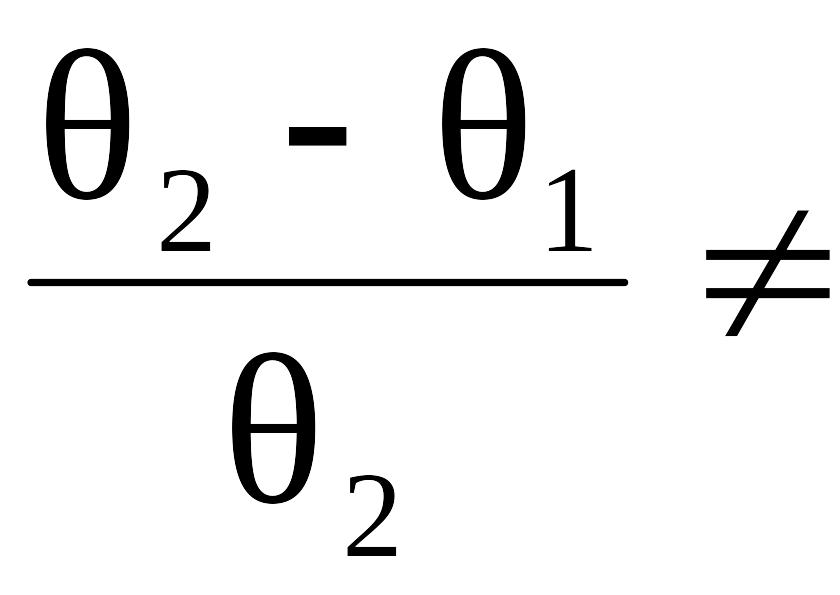0, то m₂ не является абсолютно непрерывной относительно m₁, но мера m₁ абсолютно непрерывна относительно m₂, так как m₁ = 0, когда m₂ = 0. Однако обе меры m₁ и m₂ абсолютно непрерывны относительно меры Лебега. Данное ограничение приводит к тому, что риск формирования достаточной статистики разбиения R(x), определенный в виде функционала расхождения в качестве критерия качества формирования статистики разбиения, вырождается в функционал различия, поскольку изменяется исходное предположение об однородности семейства мер. При этом

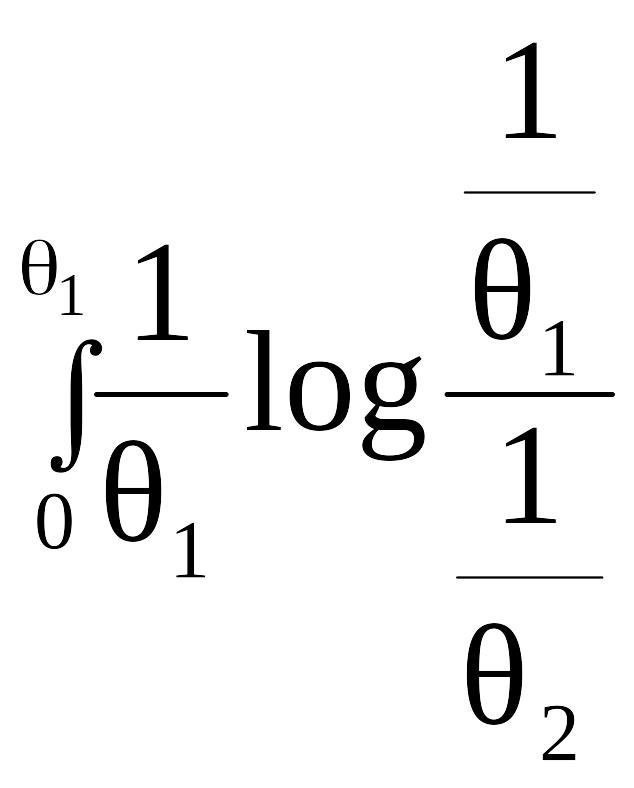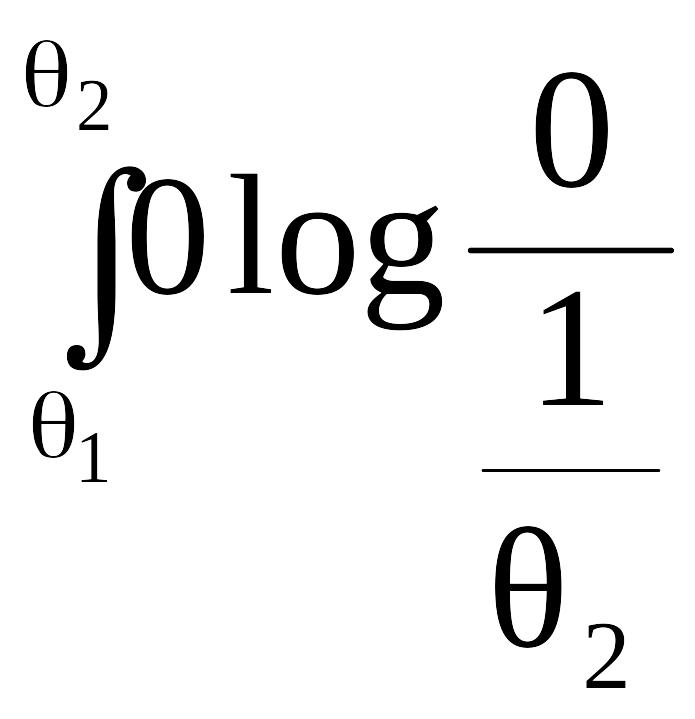R(x) = dx + dx = ,

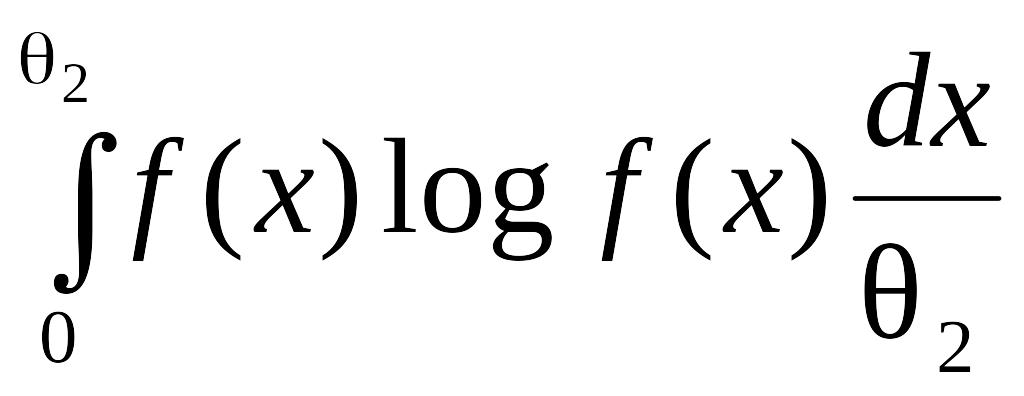где f(x) = при 0 £ x £q₁ и f(x) = 0 при q₁ £ x £ q₂, так что, учтя введенное выше смещение, получаем

R(x) = log = (logq₂ – logq₁) = H_h(q₂) – H_h(q₁), (2.26)

где H_h(q_i) – мера информации по Хартли разбиения соответствующей выборки.

Задача 2.4. Определить риск передачи сигнала на фоне аддитивного шума, относящегося к классу всех положительных непрерывных случайных величин с одним и тем же математическим ожиданием, и имеющего наибольшую энтропию.

Решение. В соответствии с экстремальным свойством экспоненциального закона распределения для решения данной задачи определим риск для экспоненциальной популяции f_i(x) = exp[– (x – _i)] (_i x  ) и f_i(x)= 0 (– < x < _i), i = 1, 2, ₁ > ₂. Находим, что

R(y, x) = log e – 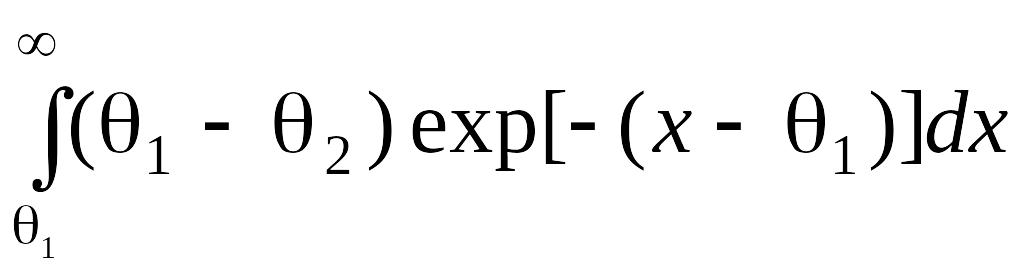= log e – ₁

xp(–x) x log edx = log e

и для выборки О_n в n независимых наблюдений R(y, x; О_n)= n R(y, x; О₁) = n(₁–₂). Известно, что если  – пространство выборок в n независимых наблюдений и Y = T(x) = min(x₁, x₂, …, x_n), то g_i(y)=n exp[–n(y – _i)], _i y  , и нулю в противном случае, i = 1, 2, является достаточной статистикой.

Задача 2.5. Определить риск для пуассоновской популяции.

Решение. Рассмотрим пуассоновские популяции с параметрами ₁, ₂. Находим, что

I(1:2) = ,

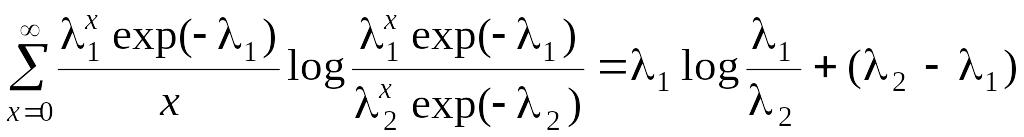и для случайной выборки О_n в n независимых наблюдений

I(1:2; О_n)=n I(1:2; О₁) = ,

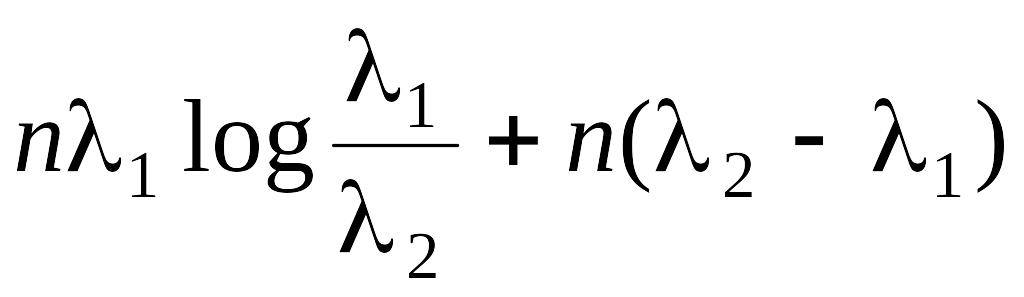и, следовательно, статистика является достаточной статистикой для пуассоновских популяций.

Определение риска оценки позволяет осуществлять синтез стратегии выбора оценок, что иллюстрируется примерами использования функционала риска при параметрическом синтезе структуры измерительного устройства.

Задача 2.6. Осуществить выбор статистики оценки вероятности сбоя P_н.с устройства контроля технологического параметра с алгоритмом последовательного его оценивания. При разработке методики оценки P_н.с устройства контроля с распределенным регистрирующим контуром датчиков необходимо учесть, что величина P_н.с для разных датчиков не постоянна, поскольку зависит от разброса параметров каждого датчика. В то же время надежность оценки P_н.с. для обеспечения равных условий ее определения целесообразно выбрать от датчика к датчику одинаковой.

Описание предметной области. Функционал риска характеризует качество измерительного процесса. Чтобы продемонстрировать возможности, которые представляет функционал риска при параметрическом синтезе элементов измерительного устройства, рассмотрим использование функционала риска при синтезе измерителей скорости, которые функционируют в специализированных электрофизических установках, предназначенных для разгона метаемого объекта. Необходимость разработки таких установок определяется возрастающей опасностью поражения Земли из космоса крупными космическими телами. Такая опасность вызывает необходимость разработать противометеоритную систему защиты Земли, с помощью которой производится запуск метаемого объекта. При столкновении метаемого объекта с крупными космическими телами последние уничтожаются или разрушаются, либо переводятся на траекторию движения, исключающую поражения ими Земли. Одним из основных элементов этой системы являются электродинамические установки высокоскоростного метания объектов, на которых с помощью рельсотрона и осуществляется разгон метаемого объекта. В настоящее время за рубежом (США) возобновились работы по созданию электродинамических установок высокоскоростного метания объектов. Установки подобного типа могут быть использованы также и для доставки на орбиту Земли полезного груза (путем создания на их базе так называемого космического лифта). В этом случае электродинамические установки высокоскоростного метания объектов обеспечивают вывод на заданную орбиту Земли микрокосмических летательных аппаратов. Кроме того, данные установки могут быть использованы при исследовании состояния твердых тел в условиях высоких давлений, при испытаниях противометеоритной защиты космических аппаратов, при экологически чистом запуске микрокосмических летательных аппаратов и зондов с борта космических аппаратов для изучения космических объектов, для инициирования путем соударения при термоядерном синтезе и в других областях науки и техники.

Механизм работы электродинамических установок высокоскоростного метания объектов заключается в том, что микрокосмические летательные аппараты, взаимодействуя с разгоняемым плазменным сгустком (плазменным поддоном или поршнем), образуют совместно объект управления. Формирование плазменного поддона осуществляется путем разряда конденсаторной батареи на металлическую фольгу (затравку, установленную в начале направляющих электродинамических установок высокоскоростного метания объектов), которая при этом взрывается, образуя плазму. Полученная плазма, ускоряясь, движется по направляющим рельсотрона, установленным на изоляторах, под действием протекающего в цепи тока и ускоряет метаемый объект. При этом электродинамическая сила, создающая ускорение плазмы, приложена к электронной компоненте плазмы, так как радиальный ток в направляющих рельсотрона переносится легкими электронами, а не тяжелыми ионами. Как только под действием электродинамических сил электроны сдвигаются вдоль направляющих, возникает продольное электрическое поле, которое заставляет ионы двигаться вслед за электронами. Сила, приложенная к электронам, в конечном счете накачивает энергию в ионную компоненту. Этот механизм накачивания энергии позволяет эффективно осуществлять ускорение метаемого объекта на электродинамических установках высокоскоростного метания.

В настоящее время данная технология позволяет осуществлять на базе электродинамических установок высокоскоростного метания объектов проекты по ускорению метаемого объекта массой 1 г до скорости 12, 15, 20 и 25 км/с. Причем в комбинированной электрогазодинамической установке (при максимальном токе 400 кА, длине ускорителя 0,9 м и массе метаемого объекта 1,3 г) в воздухе, при атмосферном давлении, стабильно достигалась скорость 4,5 – 5 км/с. При увеличении тока до 500 кА в модернизированном ускорителе достигалась скорость (с частичным разрушением метаемого объекта) до 7,4 км/с.

Для обеспечения высокого качества решения баллистических задач, стоящих перед электродинамическими установками высокоскоростного метания объектов, необходимо, чтобы на вход системы управления разгоном метаемого объекта поступала высокоточная информация о достигнутой на установке скорости. В связи с этим при проектировании системы управления электродинамическими установками высокоскоростного метания объектов должна решаться в первую очередь задача проектирования измерительно-информационного комплекса по критерию, который обеспечивает минимизацию погрешности оценки, достигнутой в процессе разгона скорости. Кроме этого погрешность достигаемой при разгоне скорости определяется и качеством исполнительного органа (рельсотрона). Таким образом, погрешность решения баллистической задачи определяется точностью измерения скорости и качеством системы разгона рельсотрона.

Необходимые высокие эксплуатационные характеристики системы управления электродинамическими установками высокоскоростного метания объектов непосредственно определяются высоким качеством измерительно-информационного комплекса системы управления процессом разгона. При этом коммутации высоких энергий в системе управления порождают мощные помехи, воздействующие на измерительно-информационный комплекс и увеличивающие вероятность нарушения процесса управления, что резко снижает качество решения электродинамической установкой высокоскоростного метания объектов заданной баллистической задачи. Задача обеспечения высокого качества управления электродинамической установкой высокоскоростного метания объектов в рамках системы управления разгоном объекта предъявляет высокие требования к измерительной информации о достигнутом на электродинамической установке высокоскоростном метании объектов. В связи с этим при проектировании систем управления разгоном одной из первых должна решаться задача синтеза устройства контроля линейной скорости с распределенным регистрирующим контуром. Данное устройство контроля линейной скорости обеспечивает первичный сбор и обработку измерительной информации о разгоняемом объекте, на основании анализа которой система и принимает решение по управлению разгоном микрокосмических летательных аппаратов. Проектируемое устройство контроля линейной скорости должно обеспечивать высокую надежность используемой измерительной информации для принятия решения по управлению разгоном метаемого объекта с целью минимизации погрешности оценки, достигнутой в процессе разгона скорости. Причем функционирование данных установок сопровождается, как уже отмечалось, мощными коммутациями, которые вызывают появление мощных помех, действующих на информационные каналы устройства контроля линейной скорости.

Среди различных методов измерения линейной скорости движущегося объекта наиболее распространенным является времяпролетный метод (рис. 2.6). Он сводится к измерению временного интервала t_i, в течение которого объект перемещается между фиксированными координатами заданной траектории движения. По результатам измерения t_i вычисляется средняя скорость перемещения V_ср на заданном i-м интервале x пути между двумя соседними заданными координатами (местами установки датчиков положения объекта) по формуле

V_cpi =x/t_i.

При этом фиксация моментов прохождения объектом заданных координат в устройстве измерения скорости осуществляется распределенным регистрирующим контуром, состоящим из N датчиков положения с блоками формирования импульсного выходного сигнала. Расчет скорости по измеренным интервалам времени t_i осуществляется вычислительным блоком устройства измерения скорости.

Рис. 2.6. Структурная схема устройства контроля линейной скорости: Д_i – датчики регистрации объектов; ЭОД – элемент объединения датчиков; УОИС – устройство обнаружения информационного сигнала; ИВИ – измеритель временных интервалов; ВЫЧ – вычислитель; УОИ – устройство отображения информации

Решение. Для решения данной задачи сравним риски классической оценки P_н.с. с другими статистиками её оценки. При этом учтем, что каждый канал регистрации устройства контроля с РРК, заданный соответствующим датчиком Д_i, определяет процесс регистрации сигнала, который характеризуется случайной величиной X_i. Величина X_i реализуется либо событием А – правильное срабатывание выходного формирователя УОИС от сигнала датчика Д_i, либо событием В – сбой при наличии сигнала на выходе датчика Д_i с вероятностями (1–P_н.с), P_н.с.. Полное событие для всего УКЛС X = (X₁,..., X_N) определяется всевозможными сочетаниями C элементарных событий A и B для всех N каналов регистрации X = (X₁,..., X_N) = A^{N–k k}, где k – количество сбоев работы устройства контроля. Таким образом, вероятность события X = (X₁,..., X_N) имеет биномиальное распределение с параметрами (P_н.с., N)

Р_р{X=k}=C , k = 0, 1,…, N

и исходная задача оценки P_н.с. эквивалентна задаче оценки вероятности биномиального распределения по однократному наблюдению величины X.

Классическая оценка для P_н.с. как частость события сбоя устройства контроля

= N^–1 _i, (2.27)

как известно, является несмещенной, а ее риск, учитывая, что Е_pP_н.с.= P_н.с, равен

R_W( ; P_н.с.) = Е_p( )² – Е_p(P_н.с.)² = N^–1P_н.с.(1 – P_н.с.),

то есть надежность оценки P_н.с выходного формирователя УОИС устройства контроля по классической статистике зависит от P_н.с. и будет меняться от датчика к датчику. Для устранения недостатка P_н.с выходного формирователя УОИС устройства контроля применяют для оценки байесову статистику, которая имеет вид

T = =

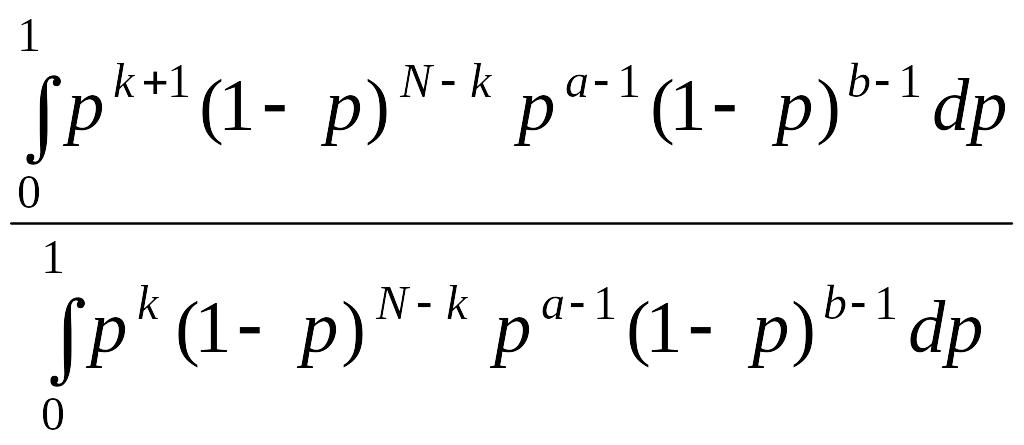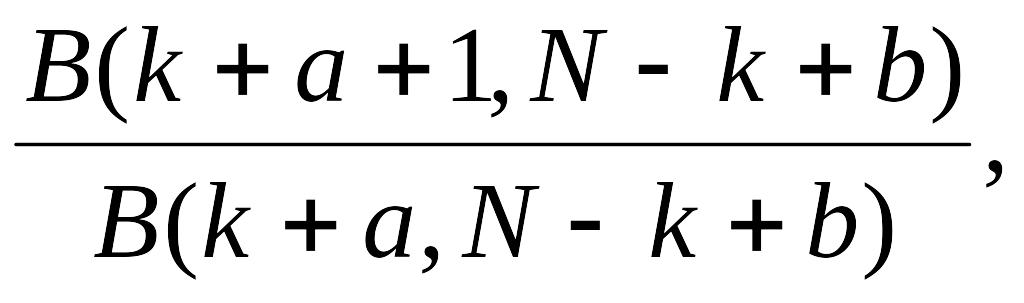
где B(.,.) – бета - функция [56]. Воспользовавшись выражением для бета – функции через гамма – функцию Г(.), получаем

T = = ,

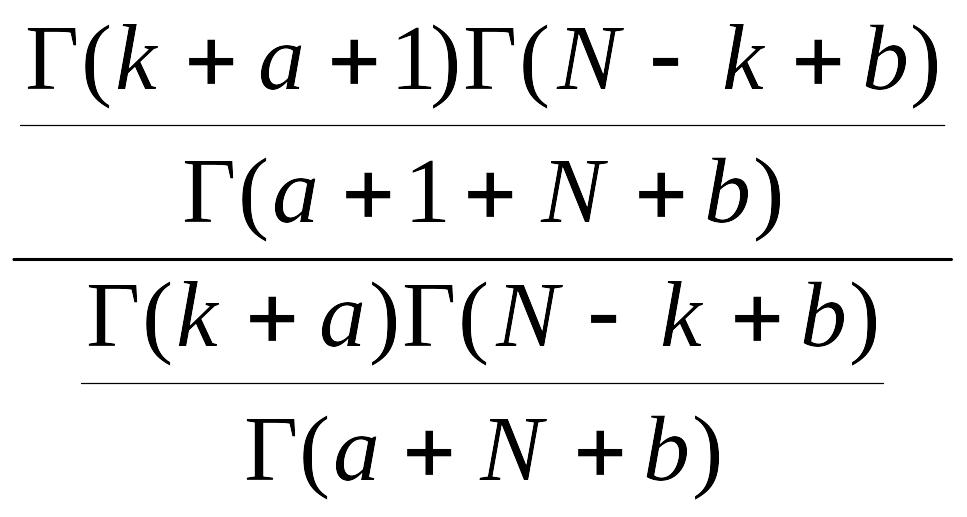где a, b – произвольные постоянные, а k = _i. Для обеспечения постоянства риска в данной статистической задаче примем а= b = =2^-1 . При этом байесовская оценка вероятности сбоя преобразуется к виду

T = 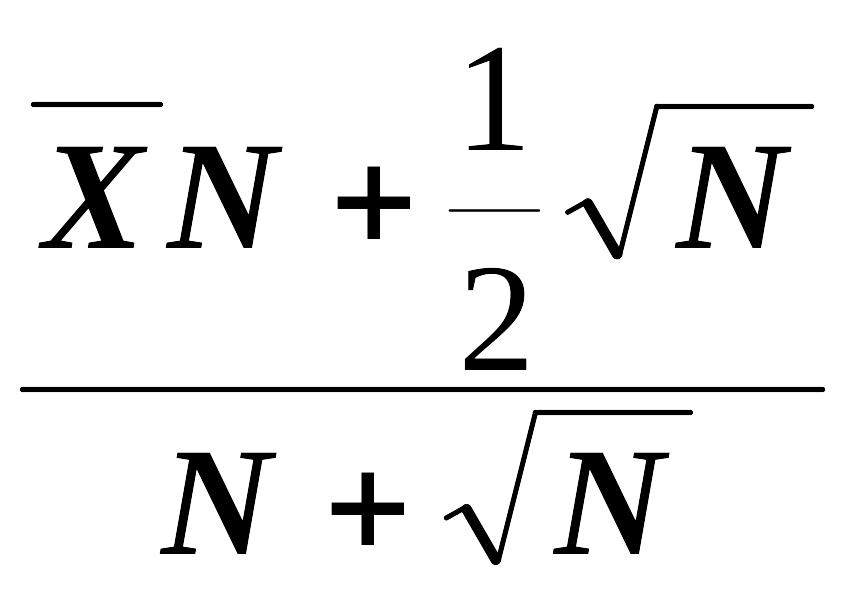= + (2( ))^–1, (2.28)

для которой риск постоянный и равен [59, 3]:

R_W(T; P_н.с.) = (2(1 + ))^–2.

Статистика (2.28) в отличие от статистики (2.27) (рис. 2.7) обеспечивает одинаковую надёжность оценки вероятности сбоя каждого канала УОИС устройства контроля. Определим области рационального использования полученных статистик, для чего исследуем области, в которых риск статистики T меньше риска классической , то есть N^–1P_н.с.(1 – P_н.с.))  (2(1+ ))^–2, которое имеет следующее решение:

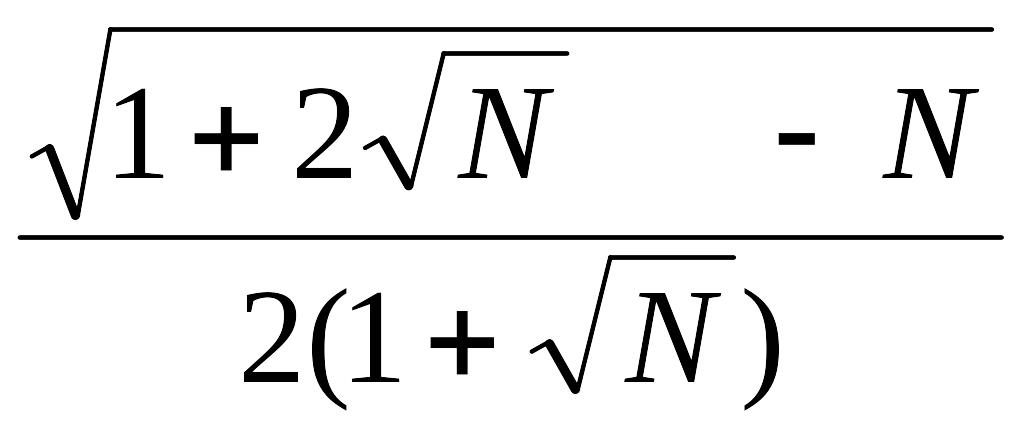 =a_N.

P

R_W( ; P_н.с.), R_W(T; P_н.с.)

Рис. 2.7. Риски оценки параметра контроля по классической P (непрерывная линия) и P модифицированной (штриховая линия) статистикам

Причем оценки параметра контроля по классической P и модифицированной P статистикам в зоне а_N отличаются незначительно (рис. 2.8).

Полученные в результате проведенного анализа выражения позволяют сформулировать следующую методику оценки P_н.с. В простейшем случае, в рамках предлагаемой методики, в качестве статистики для оценки P_н.с. может быть выбрана классическая статистика в соответствии с выражениями (2.27). Однако для обеспечения независимости риска от оцениваемого параметра (P_н.с выходного формирователя УОИС УКЛС) статистика оценки P_н.с. устройства контроля скорости должна определяться выражением (2.28). Причем стандартная статистика , в соответствии с выражением (2.27), обладает меньшим риском, чем статистика T, в соответствии с выражением (2.28), в области >а_N и большим риском в области < а_N, где a_N = 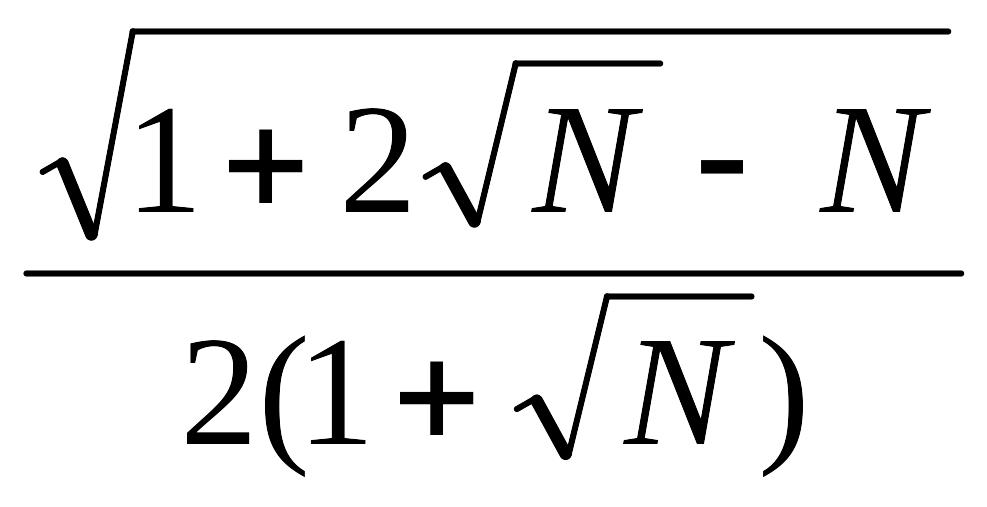. При малых N оценка Т лучше, чем , но с ростом N, наоборот, оценка предпочтительнее Т всюду, кроме интервала, длина которого стремится к нулю как N^{– 1/4}.

N

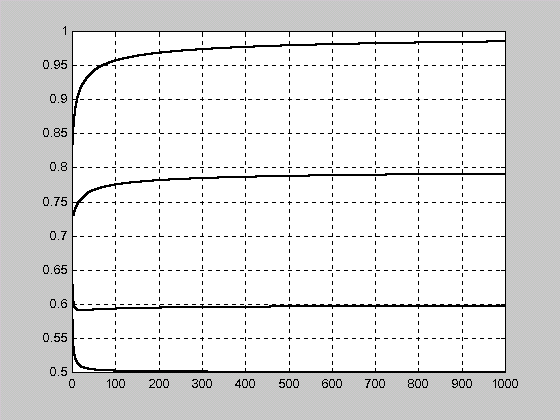
P , P

Рис. 2.8. Оценка параметра контроля по классической (штриховая линия) P и модифицированной P (непрерывная линия) статистикам

Задача 2.7. Определить закон изменения риска оценки при введении в устройство дополнительного информационного параметра.

Решение. Кроме снижения риска оценки за счет выбора соответствующей статистики определения оценки, возможно снижение риска путем использования дополнительного информационного параметра. Рассмотрим данный вариант снижения риска. Для этого выберем Y=(Y₁, ..., Y_m)– m независимых одинаково распределенных наблюдений на одномерном евклидовом пространстве R¹ с общим распределением P_() и рассмотрим задачу оценки функции E_Y_t= P_(dy). Оценка измеряемого параметра, полученная по статистике =m^-1 ,– несмещенная. Если дополнительно предположить, что E_Y_t²< для всех , и выбрать квадратичную функцию потерь, то риск статистики =m^-1 равен

R( ; )=E_(Y_i – ())²= m^-1E_(Y_i – ())²,

а риск одного из наблюдений Y_i

R(Y_i; )=E_(Y_i – ())² R( ; ).

Таким образом, при m > 1 величина риска измерения уменьшается по закону гармонической последовательности:

R( ; )= m^-1R(Y; ).