2.6. Асимптотическое оценивание пропускной способности математической модели измерения

При последовательном накоплении измеряемой информации возможно асимптотическое оценивание пропускной способности в соответствии с теоремой.

Теорема 2.6.1. Пропускная способность многопараметрической ММИ

П(P_i; f_i)  ,

где ₂( ) =1 – ,  = P(x  EH₂), ₁(E) = 1 – ,  = P(x  H₁).

Доказательство. Поскольку для устройства измерения лишь только одна k – я переменная является доминирующей, то из приведенной выше теоремы следует = 1 = P_k, а предельный объем модели равен

П(P_i; f_i) = _i(x_i)logf_i(x_i)/f(x₁,..., x_N)d(x).

В частности, для модели, состоящей из двух обособленных (независимых) переменных x_i  E и x_j  , получаем

П(P_i; f_i)= _i(x_i)logf_i(x_i)/f(x_i, x_j)d(x) _i(x _i)dx_i)logd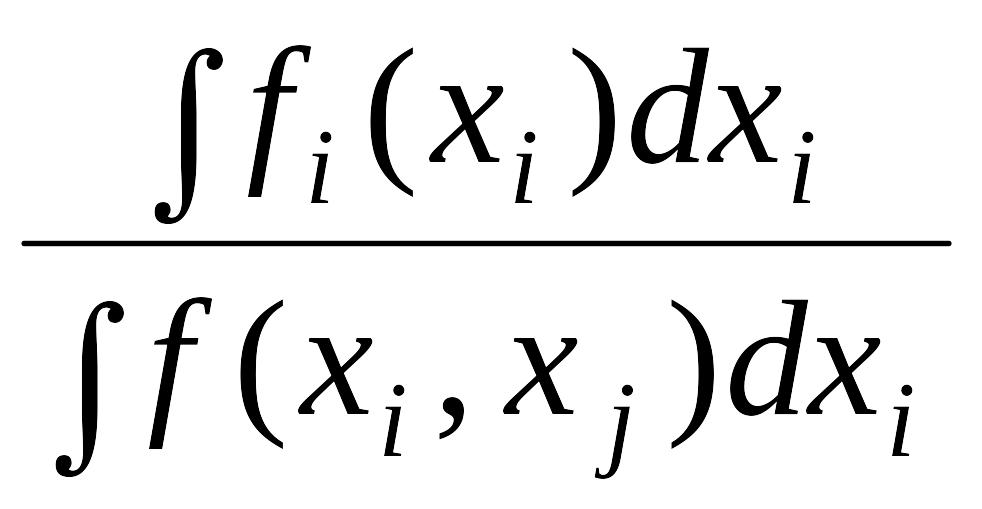 x_j

 _i(x _i)dx_i)log  = ,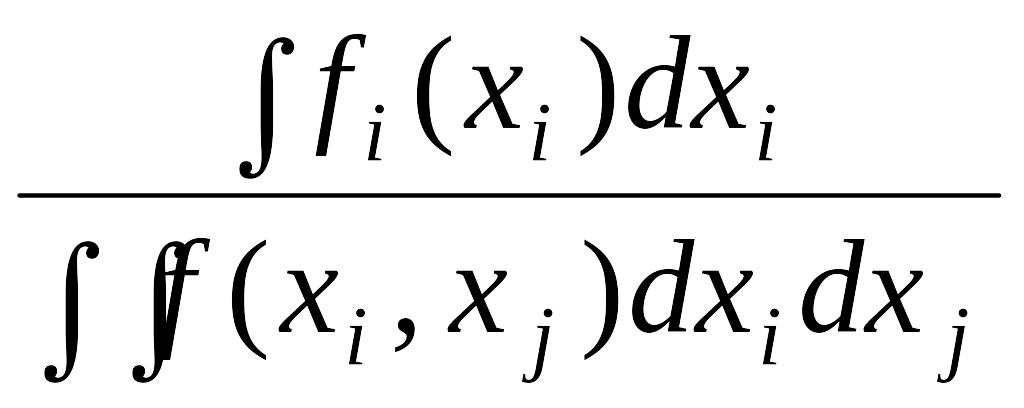

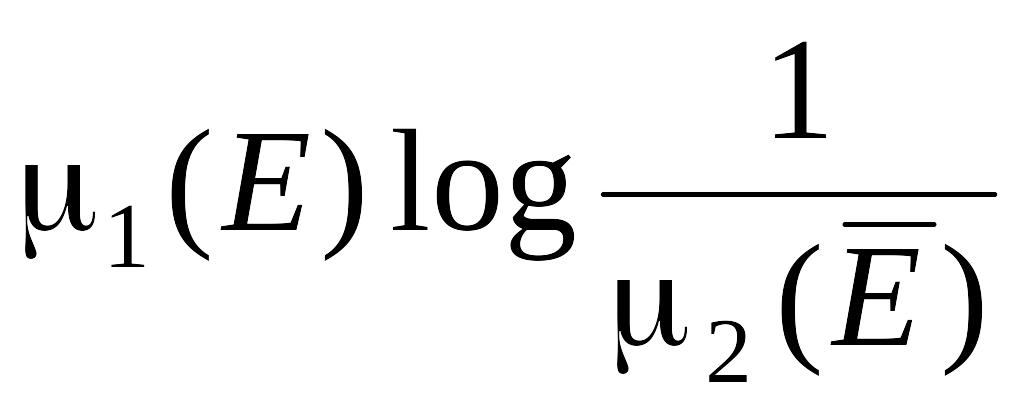где ₂( ) =1 – ,  = P(x  EH₂), ₁(E) = 1 – ,  = P(x  H₁).

Полученная в теореме 2.6.1 зависимость пропускной способности многопараметрической ММИ от вероятностей ошибок первого и второго рода приведена на рис. 2.1. Из данной зависимости следует, что при последовательном накоплении измеряемой информации увеличение ошибок требует увеличения пропускной способности устройства измерения.

R()

=1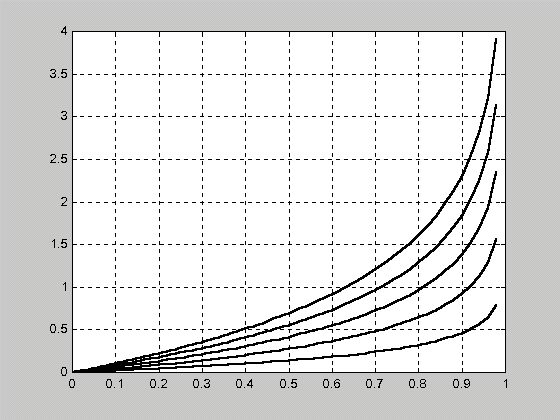

=0,8

=0,6

=0,4

=0,2



Рис. 2.1. Зависимость пропускной способности многопараметрической ММИ от вероятностей ошибок первого и второго рода при последовательном накоплении информации контроля

2.7. Асимптотический метод выделения признаков модели измерения

Выделение общей ММИ сводится к определению каждого из ее признаков, т.е. выделение соответствующего класса, который определяется областью определения этого признака в общей области определения всей модели. Таким образом, задача выделения признака ММИ, постановка которой приведена в разд. 3.3, заключается в разбиении области определения общей ММИ на области определения каждого признака. В частном случае, если область определения двухпризнаковой общей модели (пространство выборок в n независимых наблюдений) X разбита на непересекающиеся множества E и (Е = 0, X = E ) индикатором множества _E(x). Причем процедура разбиения заключается в том, что если выборка xE (_E(x)=1), принимается гипотеза H₁ (отвергается H₂), и если выборка x (_E(x)=0), принимается гипотеза H₂ (отвергается H₁). Гипотеза H₂ рассматривается как нулевая гипотеза, а E является критической областью. Вероятность неправильного принятия гипотезы H₁, ошибка первого рода, равна =P(xE₁H₂)=₂(E₁), а вероятность неправильного принятия гипотезы H₂, ошибка второго рода, равна  = P(x E₂H₁) = ₁(E₂).

При этом риск разбиения, в соответствии с теоремой 3.1 [66], которая определяет условия минимума различающей информации, для статистики Т(x)=_E(x) определяется выражением

R_р(1:2) 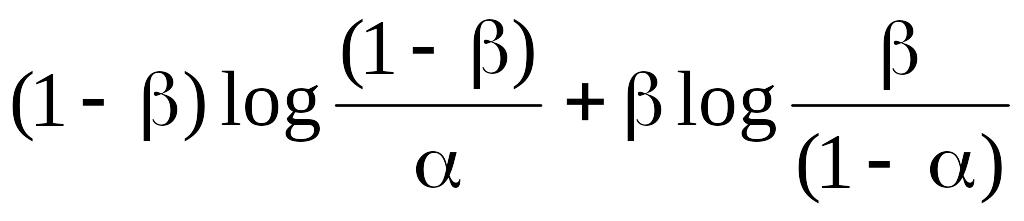 (2.20)

с равенством, совпадающим с минимумом, при

f₁(x) =

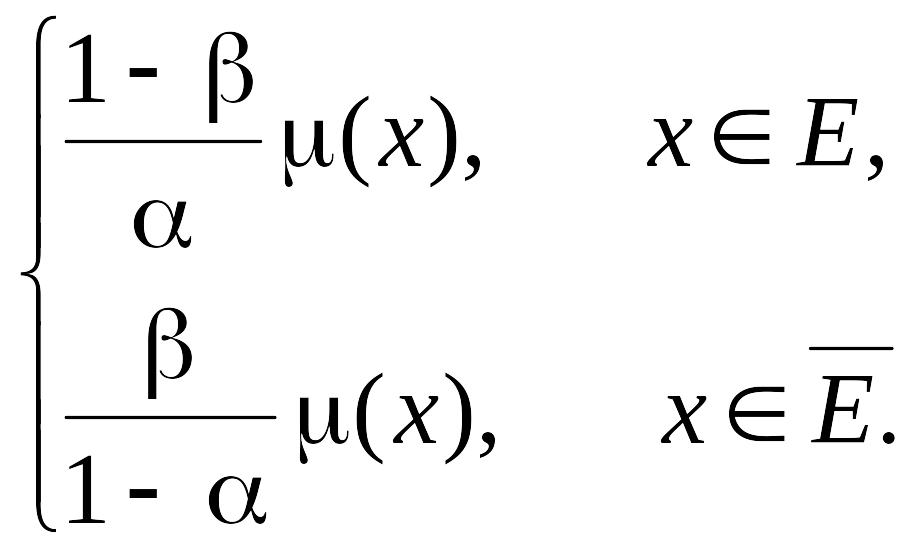
Установленные в данном выражении зависимости риска разбиения от вероятности ошибки первого и второго рода при последовательном накоплении информации измерения приведены на рис. 2.2 и 2.3 соответственно.

Данные выражения позволяют разбивать пространства X с ошибками ,  без потери информации, поскольку это разбиение достаточное. Причем риск выбора модели для соответствующих переменных при заданных значениях ошибок их идентификации ,  по областям определения можно получить, равным нулю (рис. 2.2, 2.3). В общем случае, если E_i  S, i = 1,2,..., E_i  E_j и X = E_i, т.е. если Х разбито на попарно непересекающиеся множества E₁, E₂,..., то в соответствии со следствием 3.3.2 [66]

R_р(1:2)  ,

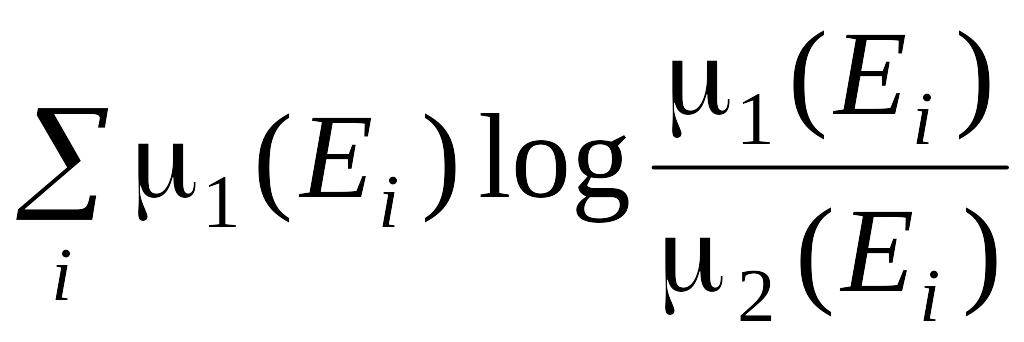а равенство достигается при условии

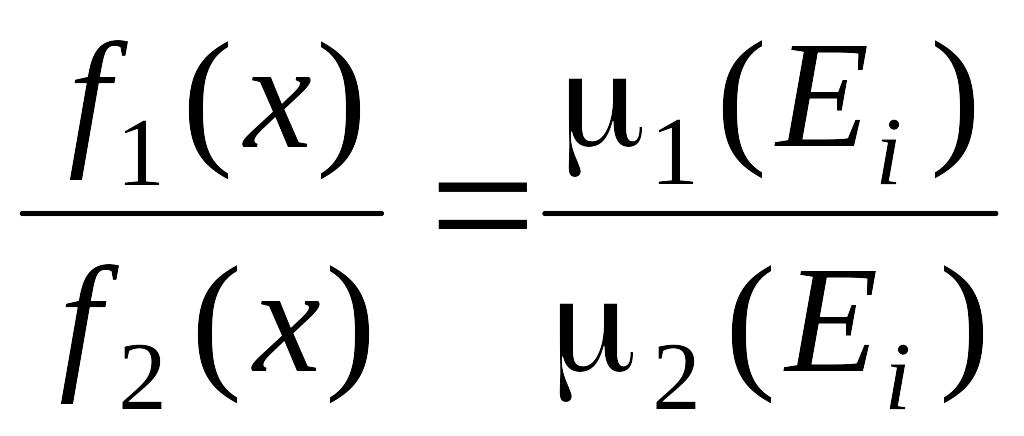
для x  E_i, i = 1, 2,...

R()



Рис. 2.2. Зависимость риска разбиения от вероятности ошибки первого рода при последовательном накоплении измерительной информации

=0,2

=0,4

=0,6

=0,8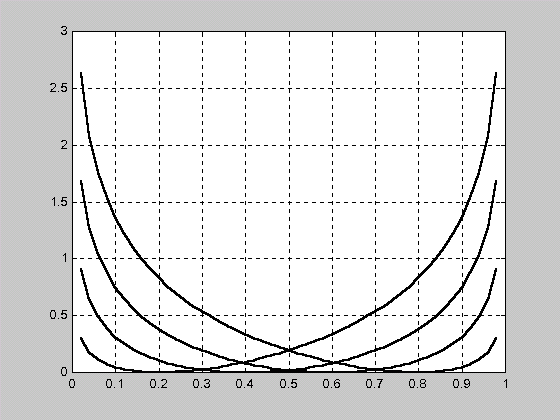

R()



Рис. 2.3. Зависимость риска разбиения от вероятности ошибки второго рода при последовательном накоплении измерительной информации

=0,2

=0,4

=0,6

=0,8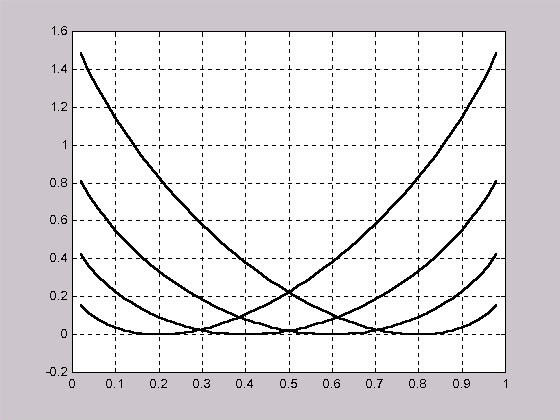

При оценке качества асимптотического выделения признака ММИ методом последовательного анализа, необходимо использовать теорему 4.3.1 [66], которая совпадает с выражением, полученным в разделе 3.8.

Теорема:

R_р(O_n) = nR_р(O₁)  log + (1 – )log ,

где O_n – выборка в n независимых наблюдений, а O₁ – выборка, состоящая из одного наблюдения.

Для фиксированного значения , скажем ₀, 0 < ₀ < 1, нижняя граница минимума всех возможных  = _n* получается из формулы

R_р(O₁)  n^–1₀log + (1 – ₀)log .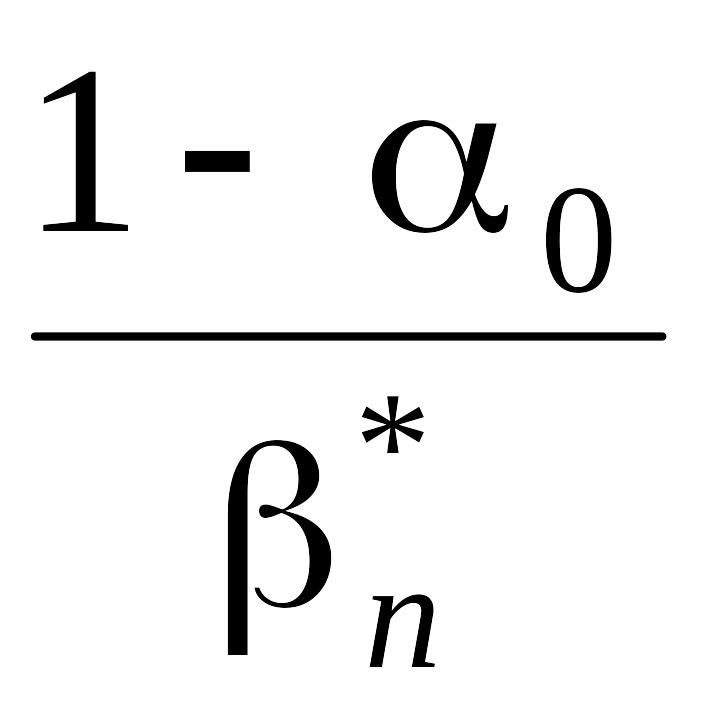

Аналогично, для фиксированного значения ₀, 0<₀<1, нижняя граница , _n* получается из формулы

R_р(O₁)  n^–1₀log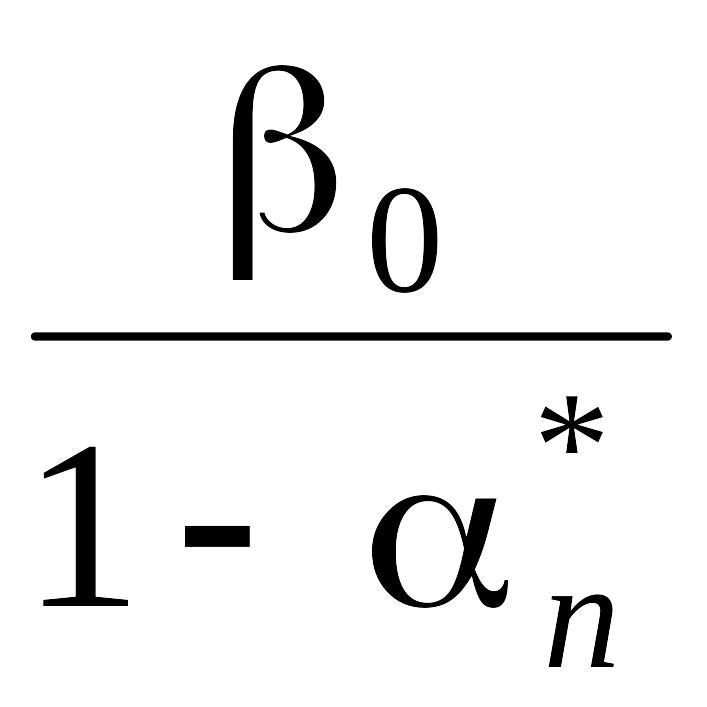 + (1 – ₀)log .

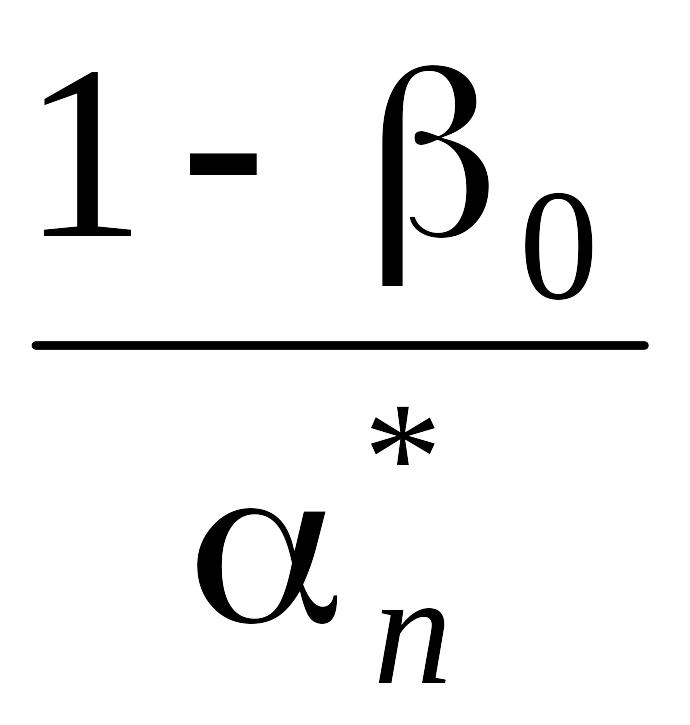Величины R_р(1:2; X)/R_р(1:2; Y) и R_р(2:1; X)/R_р(2:1; Y) могут быть использованы (для больших выборок) как мера относительной эффективности конкурирующих переменных X и Y в том смысле, что

R_р(1:2; X)/R_р(1:2; Y) = n_y/n_x или R_р(2:1; X)/R_р(2:1; Y) = N_y/N_x,

где n_x, n_y и N_x, N_y – соответственно объемы выборок, необходимых для того, чтобы получить для данного ₀ то же _n* и для данного ₀ – то же _n*.