2.5. Оценка информационного объема и риска модели измерения

Определение количества информационных переменных ММИ. Пропускная способность П статистического эксперимента, полученная в соответствии с его теоретико-информационной моделью [3], позволяет определить количество информационных переменных ММИ, необходимых для получения достаточной входной информации. Для этого определим объём передачи информации модели как разность между энтропией входов (априорной неопределенностью) и средней условной энтропией входов на выходе (апостериорная неопределенность), причем в общем случае каждый из входных параметров характеризуется вероятностью его появления на i-м входе P_i:

П(P_i, f₁,..., f_n) = H(y) – H(yx),

где априорная неопределенность H(y) и апостериорная неопределенность H(yx) определяются следующими выражениями:

H(y)=– P(H₁)logP(H₁)–....–P(H_n)logP(H_n)= –P₁logp₁–...–P_nlogp_n, (2.16)

H(yx)=– P(H₁x)logP(H₁x)+P(H_nx)log(H_nx))f(x)d(x), (2.17)

в которых f(x) = P₁f₁(x) + P₂f₂(x) +...+ P_nf_n(x). Мера связи между входными и выходными переменными, используя последние выражения для (2.16) и (2.17), определяется в виде

П(P_i; f_i) = P₁f₁(x)log + ... + P_nf_n(x)log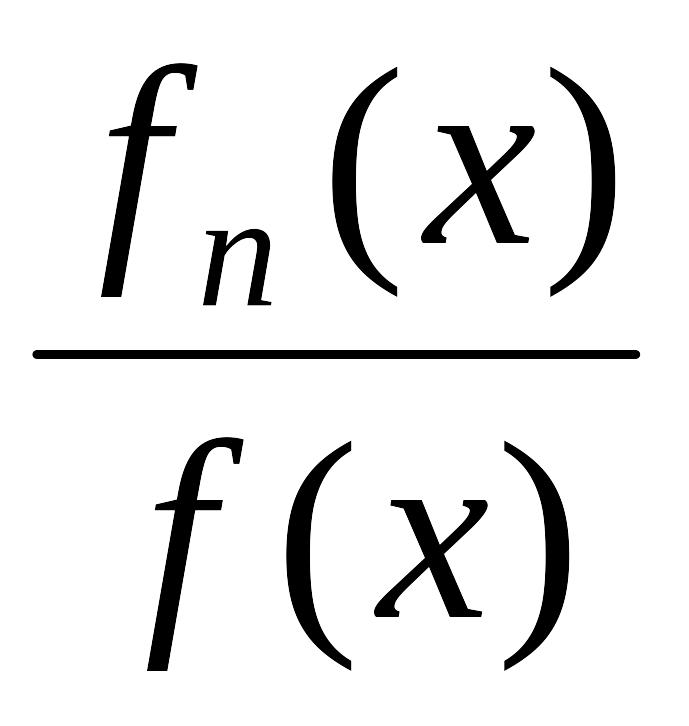 }d(x)  0,

где P(H, x)d(x) = P(Hx)f(x)d(x) – совместная вероятность H и x. Отметим, что _i(H, x)log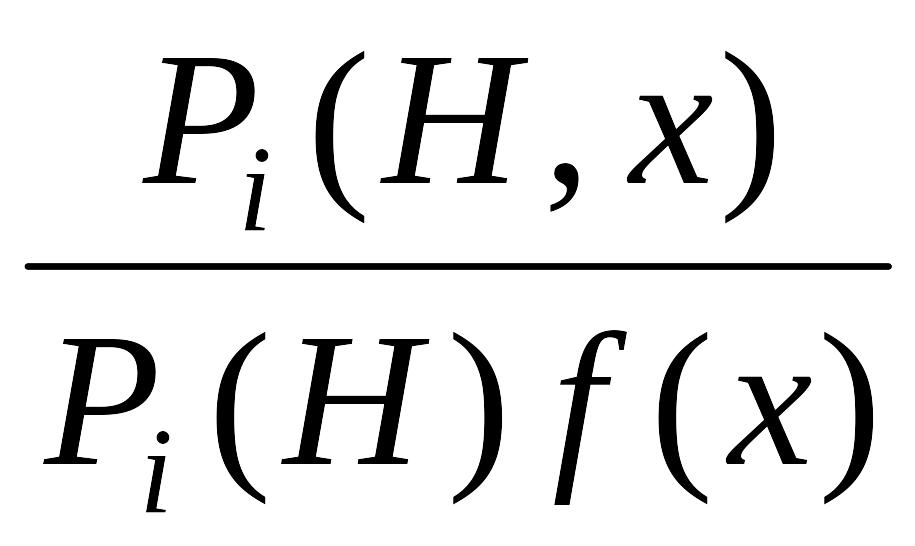 d(x) может быть определена как средняя информация в X относительно H.

Исследуем выражения для априорной информации в виде пропускной способности модели. Пусть f_i(x), i = 1, 2,..., n – плотности распределений, принадлежащих однородному семейству вероятностных мер, а P_i, i = 1, 2,..., n, таковы, что

P₁ + P₂ +...+ P_n = 1. (2.18)

Теорема 2.5.1. Максимум величины

П(P_i; f_i) = P_if_i(x)log ]d(x)

по всевозможным наборам P_i достигается для таких P_i, что

₁(x)log d(x) = ₂(x)log d(x)=...= _n(x)log ]d(x) (2.19)

и П(P_i, f_i) = n равен этой общей величине.

Доказательство. Взяв производную от dП(P_i; f_i)/dP_i (учтя выражение (2.18)) и приравняв ее к нулю получаем, что

_j(x)log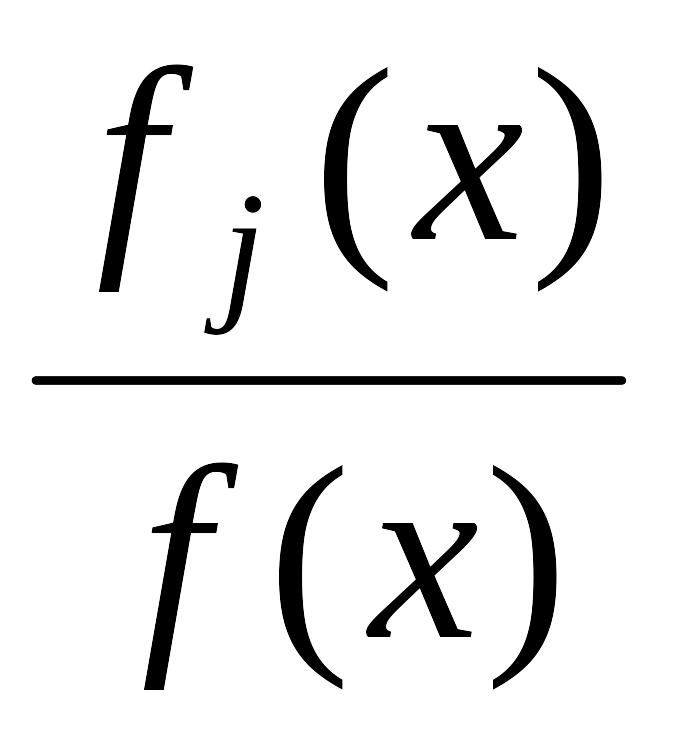 d = _if_i(x)[log ]d. =

= _if_i(x) f_i(x) 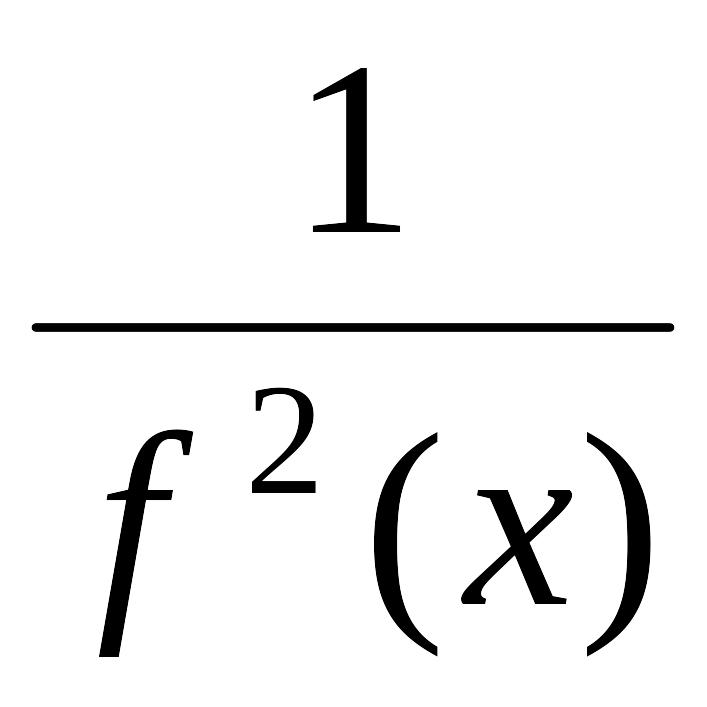f_j(x)d. = _j(x)d = 1.

Из данного выражения и следует условие (2.19). Из данной теоремы вытекает следствие, которое связывает структуру ММИ и пропускную способность эксперимента, соответствующего ММИ.

Следствие 2.5.1. Многопараметрическая модель измерения, включающая n признаков с плотностями распределения f₁(x),..., f_n(x), i = 1, 2,..., n, характеризуется максимальной пропускной способностью при условии равенства расхождений между моделью и каждым её признаков.

Определение риска синтеза многопараметрической линейной ММИ. Пусть в общем случае f_i(x_i), i = 1, 2,..., n – плотности распределения признаков x_i ММИ, а f(x₁, х₂,..., х_n) – плотность распределения, порожденная линейной ММИ

y = a₁ x₁ + a₂х₂ +...+ a_nх_n + a₀,

причем p(x₁, х₂,..., х_n) есть плотность распределения, порожденная истинной ММИ, принадлежащая к тому же семейству вероятностных мер [84]. При этом ММИ определяет теорема эмерджентности, доказательство которой приведено в [3].

Теорема (эмерджентности) 2.5.2. Для различения истинной модели измерения, заданной посредством плотности распределения p(x₁, х₂,..., х_n), линейная модель, которая состоит из n признаков с плотностями распределения f₁(x₁),..., f_n(x_n), данная посредством плотности распределения f(x₁, х₂,..., х_n), содержит информацию меньшую или равную сумме информации, доставляемой признаками модели, т.е.

f_i(x_i)logf_i(x_i)/p(x₁, х₂,..., х_n)]d(x_i) 

 f(x₁, х₂,..., х_n)logf(x₁, х₂,..., х_n)/p(x₁, х₂,..., х_n)]d(x₁, х₂,..., х_n)

с равенством при условии .

Поскольку многопараметрическая ММИ, удовлетворяющая данной теореме, обладает максимальной пропускной способностью, то она характеризуется минимальным риском для линейной модели. В связи с этим, воспользовавшись введенным в разд. 2.1 понятием риска ММИ параметра и используя свойство аддитивности функционала риска, можно сформулировать следствие.

Следствие 2.5.2. Минимальный риск R_ЛМ многопараметрической линейной ММИ для признаков с интенсивностью риска каждой компоненты модели _i характеризуется интенсивностью риска:

.

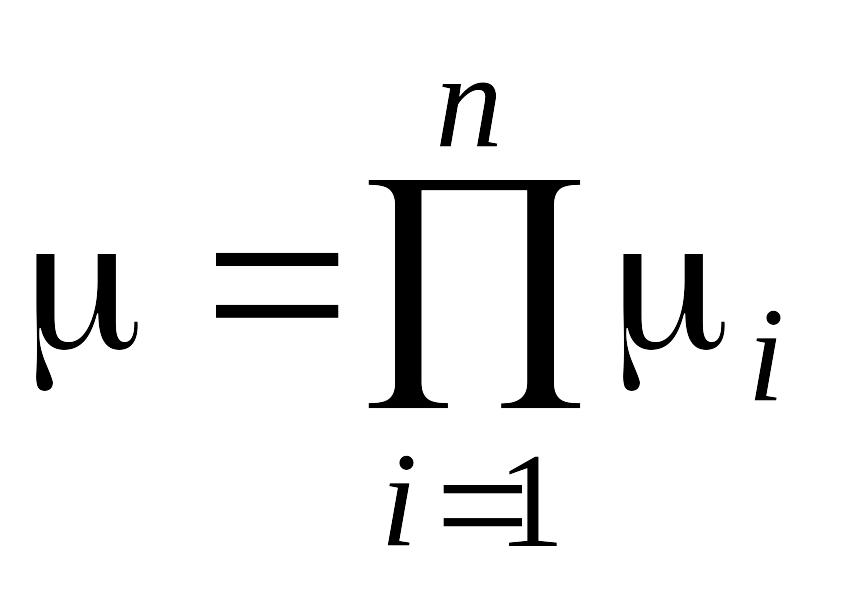Риск многопараметрической линейной модели измерения задается предельным значением риска выбора модели измерения параметра, которое получено в разд. 1.5 и определяется интегральными вероятностными параметрами.