2.4. Расчет информационной меры изоморфности

Расчет риска выбора модели по формулам §2.3 и равенствам (2.1), (2.2) и (2.3) показывает, что для построения байесовской оценки ^б необходимо полное статистическое описание процессов х и у, т. е. использование функции p(x) и условной плотности распределения вероятностей p(Y |х). Обычно известны числовые характеристики законов распределения, поэтому представляет интерес получение приближенных методов расчета, базирующихся на использовании характеристик, получаемых при определении вычислительной модели АОЭИ. При оценке состояния объекта по его модели при статистике T(x) можно использовать предельное значение риска, которое, в соответствии с теоремой о минимуме различающей информации [66] для двух плотностей распределения (произвольной f₁(х) и фиксированной плотности распределения (х) случайной величины х  Х), достигает минимум при

f(x) = (x)exp[–kT(x) – l – 1],

где k, l – произвольные коэффициенты Лагранжа.

Из данного выражения следует, что плотность вероятности f(x) порождает экспоненциальное семейство распределений, определяемое посредством (x). При этом нормированный риск модели не превышает

R₁  Q – logМ₂(), (2.12)

где М₂() = (х)еxpT(x)dх; Q = (x)f(x)dx = dlogM₂()/d.

При решении задачи выбора переменной модели, представим определяемую переменную статистикой T(x) = _E(x) в виде характеристической функции (индикатор множества [0, х₀), то есть _E(x) = 1 для х[0, х₀) и _E(x) = 0 для х > x₀).

При этом из выражения (2.12) предельное выражение для нормированного риска при

М₂() = (х)еxp_E(x)dх = еxp (x)dx

и Q = 1 имеет вид

R₁   – log [еxp (x)dx] = –log (x)dx. (2.13)

Для окончательного получения выражения для оценки риска выбора модели определим интенсивность риска, для чего введем одну из широко распространенных моделей риска – модель пропорционального риска, которой соответствует линейная зависимость (x, x₀) = x (x₀). Введенное понятие риска при пропорциональной его модели, позволяет сформулировать теорему, определяющую скорость выхода параметров, характеризующих состояние объекта за заданный уровень x₀ [79].

Теорема 2.4.1. Условное математическое ожидание M^* параметра x изменяется за заданный уровень x₀ для пропорциональной модели риска со скоростью dM^*(x)/dx (определяемой по формуле (2.14)).

Доказательство. Пусть f(x) – плотность распределения параметра в начальный момент в неоднородной группе некоторых объектов. Обозначим через А(х₀) = (s)ds интегральную интенсивность, тогда согласно формуле Байеса, для условной плотности распределения имеем

f(x|х > х₀) = f(x)exp[–xА(х₀)]/ (x)exp[–xА(х₀)]dx,

а для

M^*(х₀) = f(x) exp[–xА(х₀)]dx/ (x)exp[–xА(х₀)]dx.

Дифференцирование величины M^*(х₀) по х₀ дает

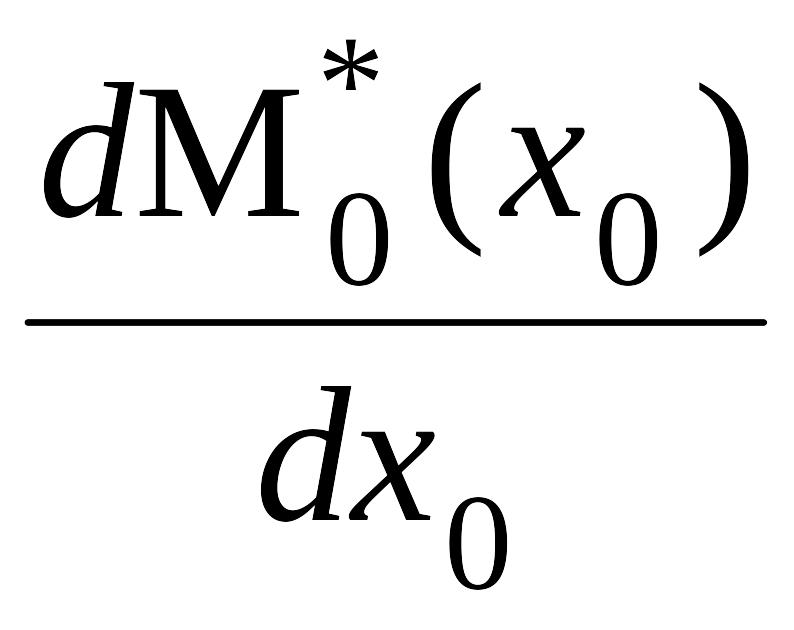= [– ² (х₀)f(x)exp[–xА(х₀)]dx]/[ (x)exp[–xА(х₀)]dx] +

+  (х₀)f(x)exp[–xА(х₀)]dx]²/[ (x)exp[–xА(х₀)]dx]².

После простых преобразований получаем

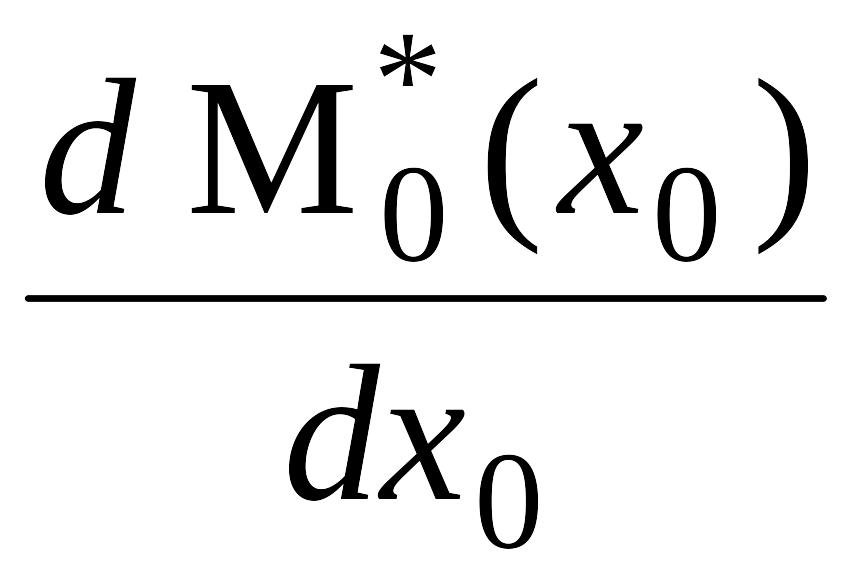= – (х₀) ₀², (2.14)

где ²₀ = Е{(M – M^*(х₀))²|х > х₀} является условной дисперсией величины M^* и поэтому неотрицательной функцией параметра х. Поскольку производная функции M^*(х₀) отрицательна, то средняя величина выхода на интервале задания M^* убывает при увеличении х₀.

Из выражения (2.14), используя условия нормирования, имеем

1 – 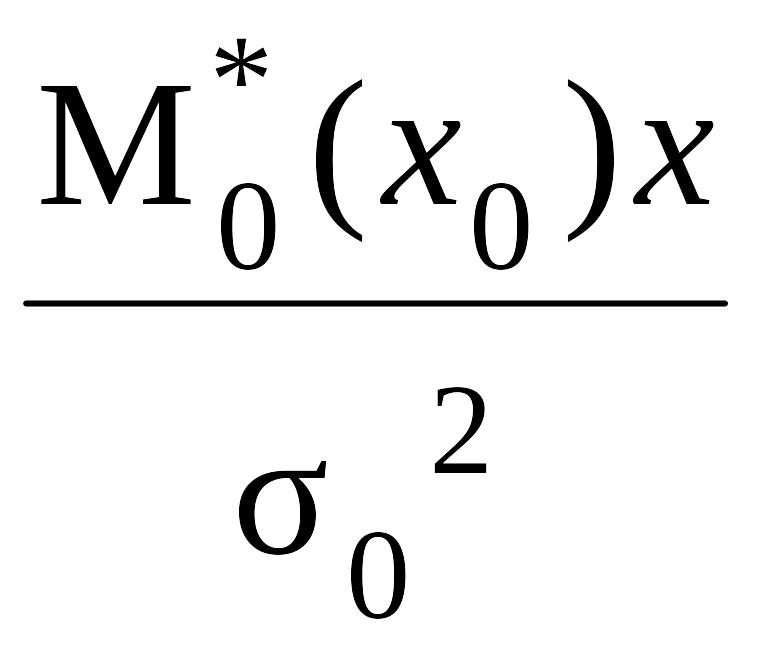= (х₀, x)dx₀. (2.15)

Полученная мера степени изоморфности дает возможность количественно оценить степень наших знаний о ПП по полученной в результате идентификации математической модели. Достоинство этой меры степени изоморфности модели состоит в том, что для ее расчета используются величины, которые определяются при идентификации. Причем поскольку оценки, определяющие параметры  и М , характеризуются риском оценивания, то можно утверждать, что риск выбора модели определяется риском оценки данных параметров, который, в свою очередь, может быть оценен функционалом эмпирического риска [42, 1, 80].