2.2. Формирование критерия качества гомоморфной математической модели измерения

Целью формирования ММИ ПП А (рис. 1.1) является его описание M_А на каком - либо формальном языке, позволяющее изучать поведение реального ПП при помощи формальных процедур [4]. ММИ M_А должна воспроизводить отношения, существующие в ПП, и частично ему гомоморфна. Формально ММИ для ПП А {E_А, R_А}, который характеризуется множеством объектов E_А и отношений R_А на множестве данных объектов, можно представить в виде M_А {E_M, R_M}, где E_M, R_M – элементы модели, соответственно множество объектов E_M ММИ и отношений R_M на E_M.

Формирование конкретной ММИ из общей осуществляется в соответствии с желаемым уровнем ее адекватности реальному ПП. Уровень адекватности достигается путем воспроизведения свойств и отношений, существующих в реальном ПП, на его ММИ. Для синтеза модели сложных ПП или датчика в целом осуществляется ее декомпозиция на совокупность ММИ E , разработка ММИ каждого элемента общей ММИ, введение их иерархии, потоков информации между ними и их согласование.

Если определены алгебраические описания ММИ M_А={E_M, R_M} и ПП А = {E_А, R_А}, то при построении модели M_А имеет место нечеткость отображения E_А, R_А в E_M, R_M. Адекватность модели M_А ПП осуществляют путем сравнения выходов y_M ММИ M_А и выходов y_А ПП А при известном входе. Причем через величину разности y= y_M – y_А можно определить функцию потерь, которая служит оценкой точности ММИ и определяет ее риск [1], а адекватность ММИ ПП можно выразить количественными оценками:

К_э(e ) = ^k, 0   1, k = , k* – количество элементов;

К_о(Г , ) = ^k, 0   1, l = , l* – количество отношений.

При этом значение  имеет смысл оценки истинности отражения в e , а  – истинности отражения отношения в Г . Если объекты моделирования и отношения имеют разную важность (веса a^k, b^l) в ММИ M_А, то в качестве оценки адекватности ММИ M_А ПП А, полученной путем композиции составляющих общей модели, следует использовать выражение

K_A = [ К_э(e )][ К_о(Г , )] = [ ^k] [ ^k], (2.7)

где = 1, = 1, 0  K_A 1.

2.3. Информационная мера степени изоморфности модели

Полученный общий показатель качества ММИ может быть использован для целенаправленного ее поиска в соответствии с работами [76, 84]. В качестве характеристики состоятельности выбора элемента модели заданного ПП по экспериментальным данным в выражении (2.1) используется понятие надежности как вероятности ошибочно отвергнуть модель на основании экспериментальных данных y. При этом модель М рассматривается как параметр распределения y и решается задача проверки гипотезы М = М₀ против любой из альтернатив М  М, где М₀ – модель, используемая для интерпретации результатов измерения y, М – класс альтернативных моделей. Качество АОЭИ определяется надежностью выбора ММИ, то есть изоморфностью модели результатам эксперимента, и надежностью самой операции редукции измерения, которые определяются соответствующими рисками.

Для введения меры, характеризующей степень изоморфности выбранной ММИ, воспользуемся основными положениями теории информации [66]. Риск, характеризующий принятую модель М₀  М, определяется, в том числе, уровнем неопределенности в предсказании результата, к которому может привести выбранная модель М₀ при оценке состояния объекта. Задача выбора элемента модели ПП относится к классу задач по распознаванию образов, т.е. концептуально выбор элемента ММИ сводится к распознаванию состояния X_i объекта (образа) и выбор конкретного решения на основании распознанного состояния X_i по заданной классификации стандартных моделей М. Таким образом, рассматриваемая задача принятия решения относится к классу задач обучения распознаванию образов.

В задаче выбора элемента модели функция потерь равна нулю (принята правильная модель) либо величине ошибочно принятой оценки модели (принята неправильная модель). Эта особенность задачи минимизации риска выбора элемента модели и определяет специфику данного класса задач. Определённый таким образом риск для задачи классификации позволяет, исходя из общего определения риска, приведенного в разд. 1.2, представить риск выбора элемента модели в следующем виде [80]:

R_М() = R₀ = R₀ R₁,

где R₀ – квадрат принятой оценки модели; R₁ – приведенный риск.

Для конкретизации введенного в соответствии с данным выражением понятия приведенного риска выбора элемента модели, рассмотрим функцию S(x₀) = P(х>х₀), определяющую вероятность преодоления уровня х₀ [87]. Если F(х) функция распределения случайной величины Х, то

S(х₀) = 1 – F(х₀). (2.8)

Если функция распределения F(х) абсолютно непрерывна, то обозначим через f(х) соответствующую плотность распределения случайной величины. Интенсивностью риска по элементам с распределением F(x) назовем функцию (х, x₀), характеризующую совместную плотность вероятности параметра x при условии его выхода за заданный предел x₀, которая определяется выражением (в соответствии с теоремой Байеса):

(х, x₀) = [f(x)f_2|1(x > x₀|x)]/[ (x)f_2|1(x > x₀|x)dx],

где f_2|1(x > x₀|x) – представляет собой функцию-индикатор множества x>x₀. В связи с чем

(x)f_2|1(x > x₀|x)dx = f_2|1(x>x₀|x) (x)dx

и, следовательно,

(х, x₀) =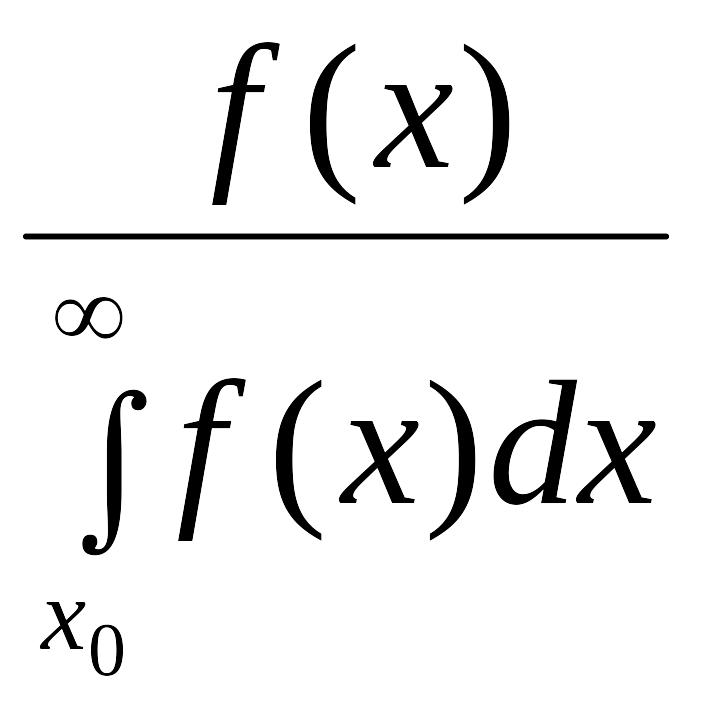 = 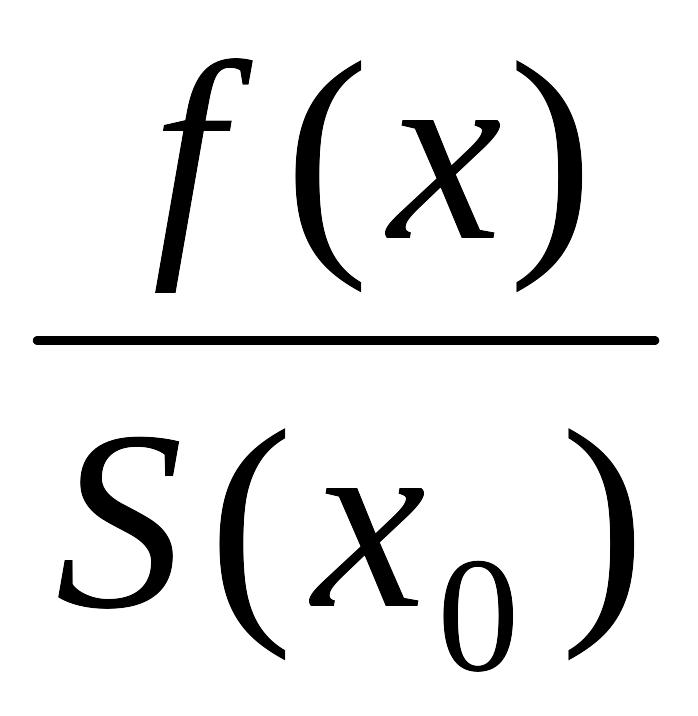. (2.9)

При этом для функции S(x₀) из уравнения (2.9), с учетом выражения (2.8), следует

S(х₀) = exp[– (х, x₀)dx]. (2.10)

Интенсивность риска характеризует вероятность выхода переменной за предел х₀ на малом интервале [x₀, x₀ + x), при условии его достижения значения х₀ P(x₀ x < x₀ + x|x > x₀) = = (x₀) x + o(x).

Определение. Под интегральной интенсивностью риска при выборе по экспериментальным данным элемента ММИ М₀М, с заданной областью ее значений D₀, понимается условная вероятность P(xD₁D₀) попадания выходных параметров выбранной модели М₀ в диапазон D₁D₀.

Таким образом, интегральная интенсивность риска выбора элемента модели характеризуется, при выбранной оценке модели, вероятностью P(x  D₁D₀) при условии, что объект находится в заданном исходном диапазоне D₀ (условная вероятность), и диапазоном D₁, в который может попасть выходной параметр модели. Интегральная интенсивность риска определяет вероятность неправильной идентификации параметра x по экспериментальным данным и равна вероятности ошибки первого рода [114].

Продифференцировав равенство (2.10) по x₀, получаем

dS(x₀)/dx₀=– (x₀)exp[– (х,x₀)dx].

После несложных преобразований имеем [ln f(x₀) – ln (x₀)] = (x, x₀)dх.

Усреднив интегральную интенсивность риска на интервале [0, х₀) по распределению f(х), получаем выражение для приведенного риска:

R₁^*(x₀) = (х₀) (x,x₀)dхdх₀ = (х₀)ln dх₀. (2.11)

Таким образом, усредненный приведенный риск на заданном интервале усреднения [0, х) совпадает с выражением для энтропии Кульбака–Лейблера [66], то есть равен “функции различения” между статическим распределением f(x) и интегральной интенсивностью риска (x), которая равна плотности вероятности выхода переменной x за заданный предел x₀, что совпадает и с интуитивным пониманием риска. Подобно можно определить риск каждого элемента модели и ее отношений, что в итоге позволяет определить риск общей модели по выражению (2.1). Полученная информационная мера изоморфности (2.11) может быть обобщена для статических многомерных и динамических моделей. При этом входными переменными модели является векторная случайная величина X (Х₁,..., Х_i,..., Х_n), а выходными – векторная случайная величина Y (Y₁,..., Y_j,..., Y_m). Тогда риск j-й выходной переменной будет равен

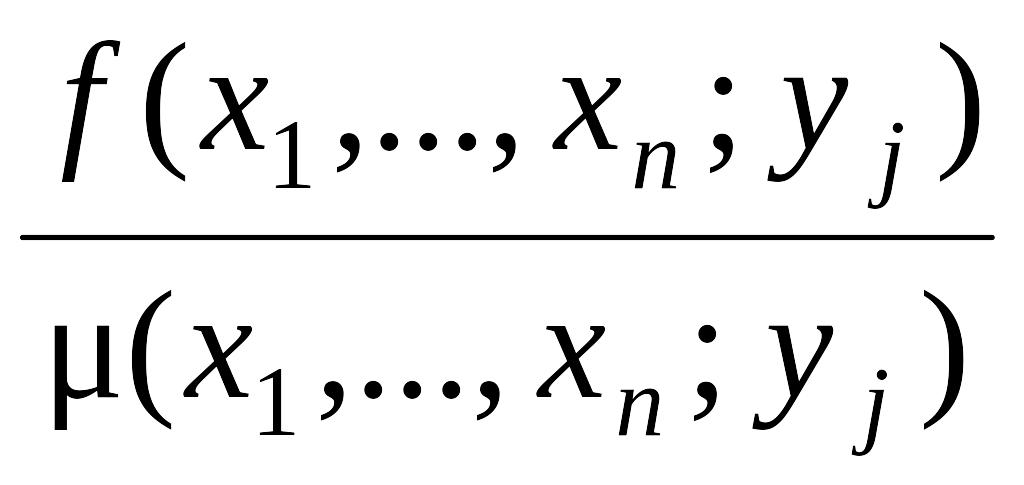R_M{Х₁,..., Х_n; Y}= R₀ (х₁,..., х_n; у_j)log dхdу.

Согласно определению, величина R_M(Х₁,..., Х_n, Y_j} характеризует неопределенность выходной величине АОЭИ, которая определяется по вектору входных величин при рассмотрении их совместного влияния на параметр Y_j. Данное выражение согласуется с выражением (2.7), которое определяет надежность композиционной модели.