Учет влияния насыщения на параметры.

При расчете влиянии параметров предыдущих режимов можно было не учитывать влияния насыщения, так как токи в этих режимах относительно малы и потоки рассеяния не создают заметного паде­ния напряжения в стали зубцов. При увеличении скольжении свыше критического и в пусковых режимах токи возрастают, и потоки рас­сеяния увеличиваются. Поэтому в расчетах задаются предполагаемой кратностью увеличение тока, обусловленной уменьшением индук­тивного сопротивления из-за насыщения зубцовой зоны. Ориентировочно для расчета пусковых режимов, принимают К_нас=1,1-1,4.

15. Средняя МДС обмотки, отнесенная к одному пазу об­мотки статора:

;

	, А	uп	а		kоб1	Z1	Z2	Fп.ср, А
Пример	26.584	28	2	1	0,958	48	38	3,357·103
Расчет
Расчет

где u_п - число эффективных проводников в пазу (п.2.2.6.),

а - число параллельных ветвей.

2.9.16. Коэффициент для определения фик­тивной индукции потока рассеяния в воздушном зазоре:

;

	СN	δ, м	t1, м	t2, м
Пример	0,978	0,0005	0,012	0,015
Расчет
Расчет

где  - воздушный зазор, выбранный в п.2.4.1.;

t₁ и t₂ - зубцовые деления статора и ротора (п.2.2.4. и п.2.4.4.).

17. Фиктивная индукция потока рассеяния в воздушном зазоре:

;

	СN	δ, м	Fп.ср, А	Вфδ, Тл
Пример	0,978	0,0005	3357	4,29
Расчет
Расчет

2.9.18. Коэффициент магнитной проводимости пазового рас­сеяния обмотки статора с учетом насыщения.

По полученному значению B_ и по таблице 46 находим отношение потока рассеяния при насыщении к потоку рассеяния не насыщенной машины, характеризуемой коэффициентом х_δ:

;

	с1	t1, м	bш1, м	хδ
Пример	3,698·10-3	0,012	0,0037	0,56
Расчет
Расчет

2.9.19. Вызванное насыщение от полей рассеяния уменьшение коэффициента проводимости рас­сеяния полузакрытого паза статора:

;

где h_ш1 - размер паза в штампе;

h₁ - размер паза в свету с учетом припуска на сборку.

	с1	h1, м	bш1, м		hш1, м
Пример	3,698·10-3	0,001	0,0037	0,229	0,002
Расчет
Расчет

2.9.20. Коэффициент магнитной проводимости пазового рассеяния обмотки статора с учетом насыщения:

;

	λп1нас	λп1	Δλп1нас
Пример	1,231	1,459	0,229
Расчет
Расчет

где _п1 - проводимость, рассчитанная без учета насыщения (п.2.6.17.).

2.9.21. Коэффициент магнитной проводимости дифференциального рас­сеяния обмотки статора с учетом влияния насыщения:

;

	λд1нас	λд1	хδ
Пример	0,879	1,569	0,56
Расчет
Расчет

где _д1 - коэффициент магнитной проводимости дифференциаль­ного рассеяния обмотки статора без учета влияния насыщения (п.2.6.16.).

2.9.22. Индуктивное сопротивление обмотки статора с учетом влияния на­сыщения:

	х1нас	х1	λп1нас	λд1нас	λп1	λд1	λл1
Пример	0,57	0,717	1,231	0,879	1,459	1,569	1,444
Расчет
Расчет

где _л1 - коэффициент магнитной проводимости лобового рассея­ния обмотки статора без учета влияния насыщения,

x₁ - индуктивное сопротивление фазы обмотки статора.

2.9.23. Коэффициент магнитной проводимости пазового рас­сеяния обмотки ротора с учетом насыщения:

;

	с2	t2, м	bш2, м	Хδ
Пример	6,03	0,015	0,0015	0,56
Расчет
Расчет

2.9.24. Уменьшение коэффициента проводимости рассеяния паза ротора:

	с2	hш2, м	bш2, м
Пример	6,03	0,0007	0,0015	0,374
Расчет
Расчет

2.9.25. Коэффициент магнитной проводимости пазового рассеяния обмотки ротора с учетом насыщения:

;

	λп2ξнас	λп2ξ	Δλп2ξнас
Пример	1,678	2,052	0,229
Расчет
Расчет

2.9.26. Коэффициент магнитной проводимости дифференциального рассеяния обмотки ротора с учетом влияния насыщения:

;

	λд2нас	λд2	хδ
Пример	1,167	2,084	0,56
Расчет
Расчет

2.9.27. Приведенное индуктивное сопротивление фазы обмотки ротора с учетом насыщения и вытеснения тока:

;

	х'2нас	х'2	λп2ξнас	λд2нас	λп2	λд2	λл2
Пример	0,64	1,016	1,678	1,167	2,781	2,084	0,6
Расчет
Расчет

2.9.28. Сопротивление взаимной индукции обмоток статора и ротора в пусковом режиме:

;

	х12п, Ом	х12, Ом	Fц, А	Fδ, А
Пример	42,513	29,049	1071	731,521
Расчет
Расчет

где x₁₂ - сопротивление взаимной индукции обмоток ста­тора и ротора (п.2.8.1.); F_ц - суммарное магнитное напряжение магнитной цепи машины (на пару полюсов) (п.2.5.16.);

F_ - магнитное напряжение воздушного зазора (п.2.5.7.).

2.9.29. Коэффициент с_1пнас.

;

	с1пнас	х1нас	х12п
Пример	1,01	0,57	42,513
Расчет
Расчет

2.9.30. Активная составляющая сопротивления правой ветви Г-образной схемы замещения (см. рис.23 ).

;

	с1пнас	r1, Oм	r'2ξ	s	aп
Пример	1,01	0,401	0,269	1	0,67
Расчет
Расчет

2.9.31. Реактивная составляющая сопротивления правой ветви Г - образной схемы замещения.

;

	с1пнас	x1нас, Oм	x'2ξнас	bп
Пример	1,01	0,57	0,64	1,22
Расчет
Расчет

2.9.32. Ток в обмотке ротора.

;

	I'2п	U1нф, Oм	ап	bп
Пример	169,103	220	0,67	1,22
Расчет
Расчет

2.9.33. Ток в обмотке ротора с учетом коэффициента с_1пнас.

;

	I1п, А	I´2, A	x12п	с1пнас	ап	bп
Пример	128,953	169,103	42,513	1,013	0,67	1,22
Расчет
Расчет

2.9.34. Ток в обмотке ротора в относительных единицах.

;

	I1п*	I1п, А	I1н, А
Пример	4,444	128,953	29,018
Расчет
Расчет

где I_1н – номинальный ток обмотки статора (п.2.2.5.).

2.9.35. Относительное значение момента М_п*.

;

	Мп*	I´2п, А	I´2н, А	KR	sн	s
Пример	1,254	158,026	26,584	1,411	0,025	1
Расчет
Расчет

2.9.36. Для определения тока повторим расчет пунктов 2.9.4. - 2.9.13., для s=s_н=0,025.

;

	ξ	hc, м	sн
Пример	0,32	0,031	0,025
Расчет
Расчет

;

где находим по рис.25

находим по рис.26

	hr, м	hc, м	φ	φ´
Пример	0,03	0,031	0,05	0,99
Расчет
Расчет

;

	qr, м	b1p, м	br, м	hr, м
Пример	0,173·10-3	7,8·10-3	3,6·10-3	0,03
Расчет
Расчет

;

	br, м	b1p, м	b2p, м	h1p, м	hr, м
Пример	3,553·10-3	7,8·10-3	3,6·10-3	0,025	0,03
Расчет
Расчет

;

	qr, м	qс, м	kr
Пример	0,173·10-3	0,177·10-3	1,023
Расчет
Расчет

;

	KR	rc, Ом	r2, Ом	kr
Пример	1,016	3,645·10-5	5,377·10-5	1,023
Расчет
Расчет

	r´2ξ	KR	r´2
Пример	0,194	1,016	0,191
Расчет
Расчет

;

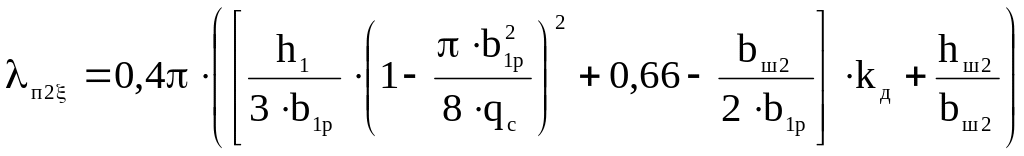	λп2ξ	h1, м	b1р, м	qc, м	bш2, м	hш2, м	kД
Пример	2,521	0,03	7,8·10-3	0,177·10-3	1,5·10-3	0,7·10-3	0,99
Расчет
Расчет

;

	λп2ξ	λл2	λд2	λп2	Кх
Пример	2,521	0,6	2,084	2,781	0,952
Расчет
Расчет

;

	х´2ξ	Kх	х´2
Пример	0,967	0,952	1,016
Расчет
Расчет

;

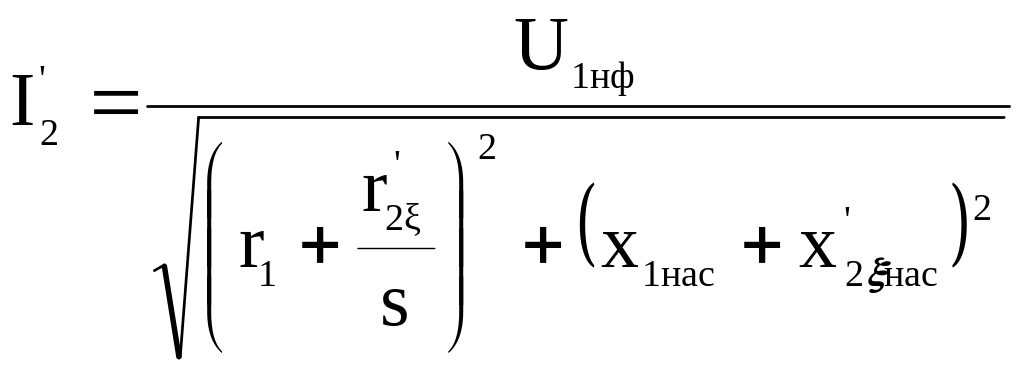	I´2, A	U1нф, В	r1, Oм	r´2ξ, Oм	sн	x 1нас, Oм	x´ 2ξнас, Oм
Пример	26,903	220	0,401	0,194	0,025	0,57	0,64
Расчет
Расчет

2.9.37. Критическое скольжение

;

	sкр	r´2	х1нас	с1нас	х´2ξнас
Пример	0,159	0,191	0,57	1,015	0,64
Расчет
Расчет

Формуляр расчета пусковых характеристик асинхронного двигателя.

№ п/п.	Расчетная формула	Единица	Скольжение
			1	0,9	0,8	0,7	0,6	0,5	0,4	0,3	0,2	0,1
1.	ξ	-
2.	φ	-
3.		-
4.		-
5.		Ом
6.	=’	-
7.		-
8.		Ом
9.		Ом
10.		Ом
11.
12.		Ом
13.		Ом
14.		А
15.		А
16.		-
17.		-

При скольжении s=1 расчитать ток и момент пусковые, при этом ток пусковой не больше заданного, а момент не меньше.

I* M*
4
3 2
2
1 1
S

0.4

0.6

0.8

0.2

1.0

0

0

49