
- •Технические характеристики си
- •1 Магазины индуктивности и емкости
- •2 Измерительный генератор
- •3 Цифровой частотомер
- •4 Многозначная мера напряжения
- •2 Опыт 1. Измерение емкости конденсатора с использованием явления резонанса
- •3 Опыт 2. Измерение емкости конденсатора методом замещения Цель расчета
- •4 Опыт 3. Измерение емкости конденсатора методом обратного замещения
- •2 Оценим предельное значение погрешности результата измерения. При расчетах используем методику примера опыта 2. Погрешность определим по формуле
- •5 Опыт 4. Измерение частоты дифференциальным методом
- •2 Для оценки предельной погрешности вычислим слагаемые правой части уравнения (5.3)
- •6 Опыт 5. Измерение напряжения методом уравновешивания
2 Оценим предельное значение погрешности результата измерения. При расчетах используем методику примера опыта 2. Погрешность определим по формуле
|
(4.1) |
где
–
![]() погрешность
настройки при выполнении первого этапа
измерения;
погрешность
настройки при выполнении первого этапа
измерения;
![]() погрешность
настройки второго этапа;
погрешность
настройки второго этапа;
![]() абсолютная
погрешность установки максимального
значения на магазине емкостей;
абсолютная
погрешность установки максимального
значения на магазине емкостей;
![]() погрешность
установки на втором этапе.
погрешность
установки на втором этапе.
2.1 Определим слагаемые уравнения (4.1)
|
(4.2) |
где
![]() .
Если частоты
и
совпадают,
то принимаем ,
.
Если частоты
и
совпадают,
то принимаем ,
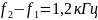 т.е. эта разность равна половине значения
ступени младшей декады частоты генератора.
Подставим выражение для
в
формулу (4.2)
т.е. эта разность равна половине значения
ступени младшей декады частоты генератора.
Подставим выражение для
в
формулу (4.2)
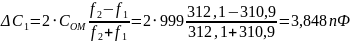

 где
–
предел допустимой основной погрешности,
см. раздел технические
характеристики СИ.
где
–
предел допустимой основной погрешности,
см. раздел технические
характеристики СИ.
 Подставим
вычисленные значения в формулу (4.1)
Подставим
вычисленные значения в формулу (4.1)

3 Оценим комбинированную стандартную неопределенность результата измерения по формуле
![]()
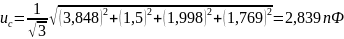
4 Запишем результат измерения
· с указанием расширенной неопределённости
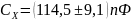 ·
с указанием комбинированной стандартной
неопределённости
·
с указанием комбинированной стандартной
неопределённости
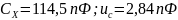
Вывод: Сравним характеристики неопределенности результатов измерений опытов 1, 2, 3. Точность измерения емкости в опыте 3 выше, чем в опыте 1, но ниже, чем в опыте 2. Увеличение погрешности по сравнению с опытом 2 объясняется тем, что погрешность установки значения меры емкости присутствует дважды при настройке в резонанс на первом и втором этапах измерения.
5 Опыт 4. Измерение частоты дифференциальным методом
Цель расчета
· Рассчитать частоту генератора по результатам измерений, полученных дифференциальным методом; · Рассчитать комбинированную стандартную и расширенную неопределенности; · Записать результаты измерения с указанием неопределенности.
Таблица 5.2 – Результаты измерения
Первое измерение |
Второе измерение |
||
|
|
|
|
51 |
125600 |
52 |
874400 |
1 Для вычисления результата измерения используем формулу (5.1) или формулу (5.2).
2 Для оценки предельной погрешности вычислим слагаемые правой части уравнения (5.3)
 где
где
![]() –
предел относительной погрешности
генератора.
Абсолютную погрешность
частотомера определим по формуле
–
предел относительной погрешности
генератора.
Абсолютную погрешность
частотомера определим по формуле
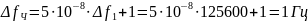
По
сравнению с погрешностью
![]() составляющей
составляющей
![]() можно
пренебречь.
Предельное значение
погрешности результата измерения
можно
пренебречь.
Предельное значение
погрешности результата измерения
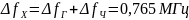 3
Стандартную неопределенность результата
измерения определим по формуле
3
Стандартную неопределенность результата
измерения определим по формуле
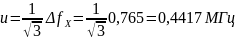 4
Запишем результат измерения
4
Запишем результат измерения
· с указанием расширенной неопределённости
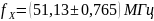 ·
с указанием комбинированной стандартной
неопределённости
·
с указанием комбинированной стандартной
неопределённости

Вывод. Дифференциальный метод позволил измерить частоту, значение которой превышает предел измерения частотомера.
6 Опыт 5. Измерение напряжения методом уравновешивания
Таблица 6.1 – Результат измерения и параметры схемы
Результат
измерения напряжения
|
Параметры схемы |
|
Номинальное
значение
|
Номинальное
значение
|
|
19,847 |
|
107 |
Примечание к таблице 6.1.
Параметры схемы в соответствии с вариантом задаются при запуске программы выполнения опыта. Границы отклонения действительных значений сопротивлений и от номинальных значений равны 1%.
При
нулевом показании гальванометра
потенциалы точек
![]() и
и
![]() равны,
следовательно, уравнение измерения
можно записать в следующем виде
равны,
следовательно, уравнение измерения
можно записать в следующем виде
![]()
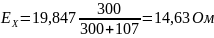
На рис. 6.2 приведена эквивалентная схема исследуемой электрической цепи.
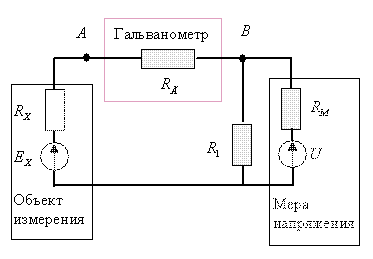 Рисунок
6.2 – Эквивалентная схема
Рисунок
6.2 – Эквивалентная схема
В соответствии с этим уравнением расширенную неопределенность результата измерения можно определить по формуле
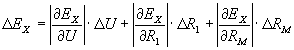
где
![]() –
граница абсолютной погрешности меры
напряжения. Граница
определяется
по заданной относительной погрешности
меры напряжений;
–
граница абсолютной погрешности меры
напряжения. Граница
определяется
по заданной относительной погрешности
меры напряжений;
![]() и
и
![]() –
границы отклонения действительных
значений сопротивлений
и
от
номинальных.
–
границы отклонения действительных
значений сопротивлений
и
от
номинальных.

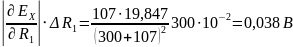
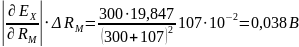
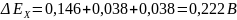
Результат измерения с расширенной неопределенностью:.


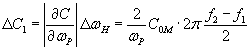 ,
,