Распределение домашних хозяйств России

по числу совместно проживающих их членов

Число членов дом. хозяйств, чел. xi	Число домашних хозяйств, fi
1 2 3 4 5 и более	192 262 226 205 115
Итого	1000

Номер медианы (1000+1)/2 = 500,5. Частоты необходимо накапливать до тех пор, пока накопленная частота не будет равна номеру медианы или не превысит его.

Таблица 4.2

Распределение домашних хозяйств России

по числу совместно проживающих их членов

Число членов дом. хозяйств, чел. xi	Число домашних хозяйств, fi	Накопленные частоты, Si
1 2 3 4 5 и более	192 262 226 205 115	192 454 680
Итого	1000

Так, 192 домашних хозяйств имеют не более одного члена, 454 домашних хозяйства – не более 2 членов, а 680 домохозяйств – не более 3 членов, т.е. 455-е, 456-е, 457-е, 458-е, 459-е, 500-е и 501-е домохозяйство состоят из 3 человек. Таким образом, медиана данного ряда равна 3 человекам, т.е. половина домохозяйств состоит из менее чем три человека, а другая половина – из более чем три человека.

Для интервального вариационного ряда медиана находится по формуле:

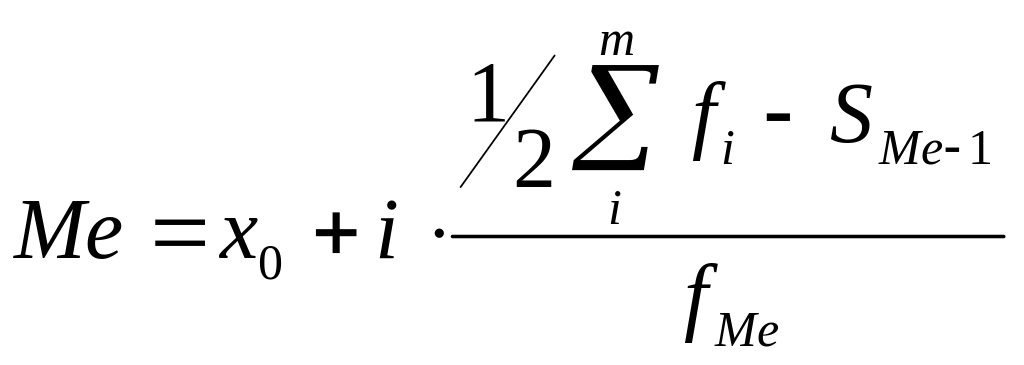, (5.8)

где x₀ - нижняя граница медианного интервала;

i - длина медианного интервала;

S_Me-1 - накопленная (кумулятивная) частота предмедианного интервала;

f_Ме - частота медианного интервала.

В симметричных рядах распределения значения моды и медианы совпадают со средней величиной: , а в умеренно асимметричных они соотносятся следующим образом: .

Рассмотренные обобщающие показатели центра распределения не вскрывают характера последовательного изменения частот, поэтому в анализе закономерностей распределения используются также ранговые (порядковые) показатели: квартили и децили.

Квартили (Q) – это значения вариантов признака, которые делят упорядоченный ряд по объему на четыре равновеликие части. Таких величин в ранжированном ряду будет три:

- первая квартиль (Q₁);

- вторая квартиль (Q₂);

- третья квартиль (Q₃).

Вторая квартиль является медианой.

Расчет квартилей основывается на кумулятивных частотах (частостях) с использованием следующих формул:

,

где , , - место квартиля (определяется для нахождения квартильного интервала),

,

,

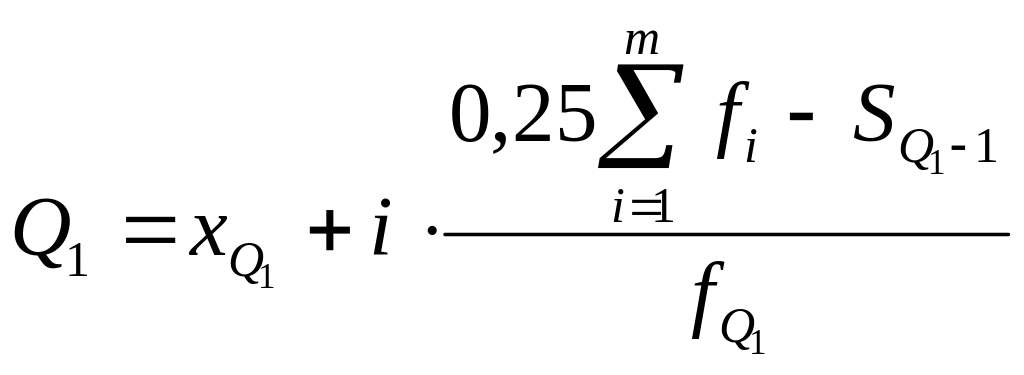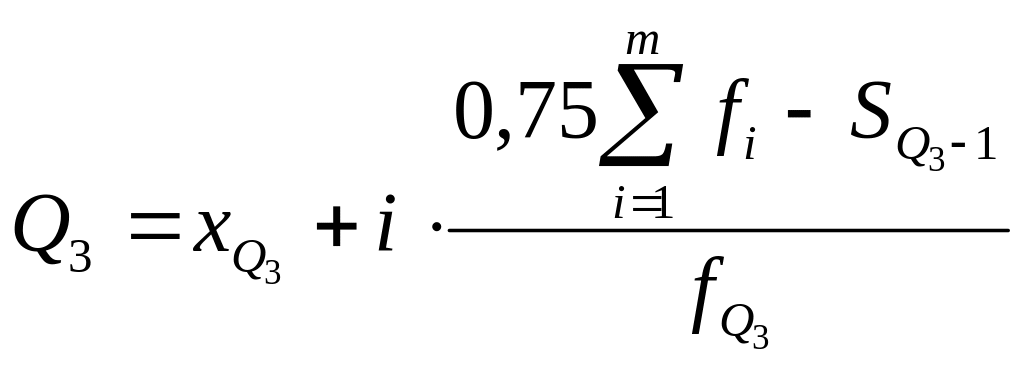где – первый или нижний квартиль,

– третий или верхний квартиль;

и – нижняя граница квартильного интервала соответствующего квартиля;

– величина (шаг) интервала;

– накопленная частота интервала, предшествующего первому (нижнему) квартилю;

– накопленная частота интервала, предшествующего третьему (верхнему) квартилю;

и – частоты квартильного интервала.

Децили – это значения вариантов, которые делят упорядоченный ряд по объему на десять равных частей. В ряду распределения выделяют девять децилий, медиана при этом является одновременно пятым децилем.

Расчет основан на кумулятивных частотах (частостях) и определяется по формулам:

,

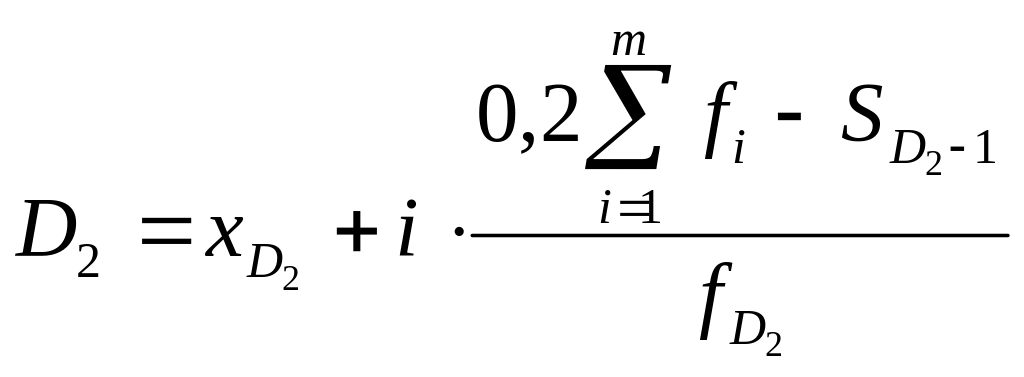
и т.д.

.

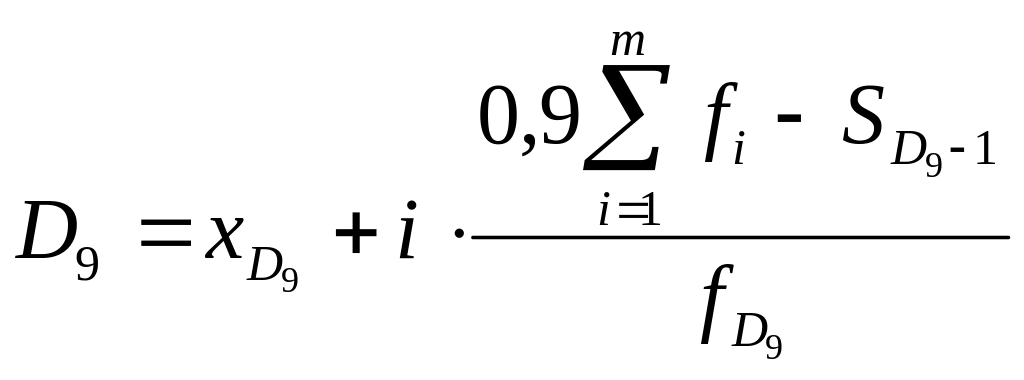Пример. Дан интервальный ряд распределения 50 учащихся по росту. Определить верхний и нижний квартиль, медиану и значения первого и девятого децилий.

Таблица 4.3