6. Относительный показатель сравнения (опСр) представляет собой соотношение одного и того же абсолютного показателя, характеризующего разные объекты (предприятия, области, страны):

Показатель, характеризующий объект А

ОПСр = --------------------------------------------------------------------- .

Показатель, характеризующий объект Б

Пример: объем производства компании «Феникс» составил за 2007г. 315 тыс. изд., а ее конкурента – 303 тыс. изд., необходимо рассчитать ОПСр.

ОПСр=315/303=1,039, т.е. объем производства за 2007 год компании «Феникс» составил 103,9% по сравнению с ее конкурентом.

3.2 Виды и свойства средних величин

Наиболее распространенной формой статистических показателей, используемой в социально-экономических исследованиях, является средняя величина. Средняя величина - это обобщенная количественная характеристика признака в статистической совокупности в конкретных условиях места и времени. Средняя величина отражает уровень признака, приходящийся на единицу совокупности.

В статистике используются различные виды средних величин. Расчет большинства конкретных статистических показателей основан на использовании средней агрегатной, средней арифметической или средней гармонической. Кроме указанных средних существуют и другие: геометрическая, хронологическая, квадратическая и т.д.

Пример: по представленным данным необходимо рассчитать среднюю заработную плату в целом по трем предприятиям:

Таблица 3.1

Заработная плата предприятий

Предприятие	Численность ППП, чел.	Месячный ФЗП, тыс. руб.	Средняя заработная плата, руб.
А	1	2	3
1 2 3	270 121 229	564,84 332,75 517,54	2092 2750 2260
Итого	620	1415,13	?

Средняя заработная плата находится через отношение совокупного фонда заработной платы к общей численности ППП.

Если в распоряжении имеются данные только гр. 1 и 2 табл. 3.1, то расчет можно провести по формуле средней агрегатной:

руб.,

где ;

x_i – i-й вариант осредняемого признака;

f_i – вес i-го варианта.

В том случае, если даны данные о средней заработной плате и численности ППП, необходимо использовать формулу средней арифметической взвешенной:

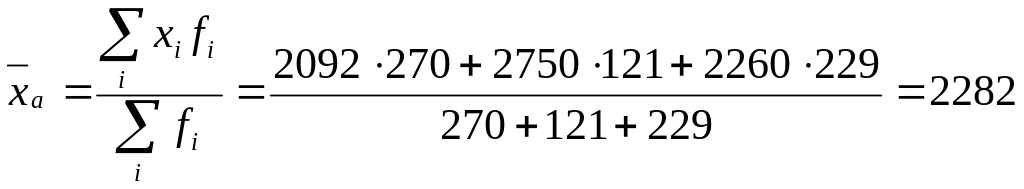руб.

Числитель формулы в данном случае позволяет рассчитать суммарный фонд заработной платы по всем предприятиям.

В отдельных случаях вес (f) представляет собой произведение двух или даже трех значений.

В тех случаях, когда:

- информация о весах отсутствует или

- каждый вариант признака встречается один раз или

- веса равны между собой,

то используется формула средней арифметической простой: ,

где n – объем совокупности.

В том случае, если бы была известна информация только о средней заработной плате на каждом из трех предприятий, расчет сводился бы к применению формулы: руб.

Допустим теперь, что в распоряжении находится информация гр. 2 и 3 табл. 3.1. В результате нам известен размер фонда заработной платы на каждом предприятии, средняя заработная плата, но не известна численность ППП. Численность ППП на каждом предприятии можно найти путем деления фонда заработной платы на величину средней заработной платы. Тогда расчет сводится к применению средней гармонической взвешенной:

,

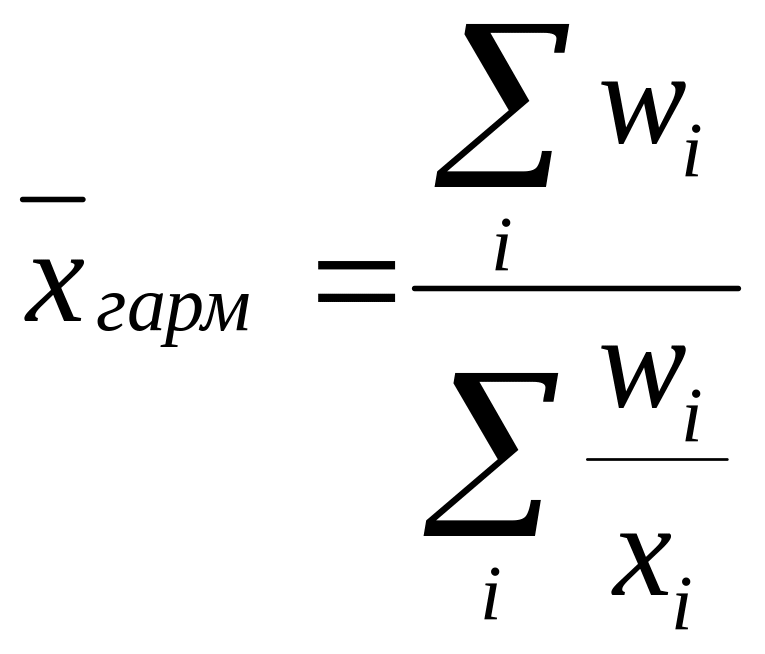где w_i – веса для обратных значений x_i.

руб.

При равенстве весов (w) расчет среднего показателя может быть произведен по средней гармонической простой: .

Основные свойства средней арифметической:

• Произведение средней на сумму ее частот равно сумме произведений отдельных вариантов на эти частоты.

• Сумма отклонений индивидуальных значений средних от средней арифметической равно нулю.

• Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины.

• Величина средней арифметической не изменится, если вес каждого варианта умножить или разделить на одно и то же число.

Следствиями этого свойства являются следующие утверждения:

а) если веса всех вариантов равны между собой, то взвешенная средняя равна простой средней

б) в качестве весов средней вместо абсолютных показателей можно использовать их удельные веса в общем итоге (доли, % ).

• Если все варианты признака увеличить или уменьшить на одно и то же число или в одно и тоже число раз, то также соответственно увеличится или уменьшится и средняя величина.

Средние показатели могут рассчитываться по дискретным и интервальным вариационным рядам. При этом расчет производится по средней арифметической взвешенной. Для дискретного ряда данная формула используется так же, как и в рассмотренном примере. В интервальном же ряду для расчета определяются середины интервалов.

Лекция 4: Показатели вариации

При изучении социально-экономических явлений и процессов статистика встречается с разнообразной вариацией признаков, характеризующих отдельные единицы совокупности. Величины признаков колеблются под воздействием различных причин и условий. Исследование вариации является составным элементом статистического анализа. В статистической практике для изучения и измерения вариации используются различные показатели (меры) вариации в зависимости от поставленных задач, к ним относятся:

- частотные показатели;

- показатели центра распределения;

- показатели степени вариации;

- показатели формы распределения.

4.1 Частотные показатели и показатели центра распределения

Частотными показателями любого ряда распределения являются абсолютная численность i-й группы – частота f_i и относительная частость d_i, где .

Кумулятивная (накопленная) частота S_i (частость S_d) характеризует объем совокупности со значениями вариантов, не превышающих Х_i. Кумулятивные частотные показатели образуются последовательным суммированием абсолютных или относительных частот, например: S₁= f₁; S₂= f₁ + f₂; S₂= f₁ + f₃ + f₂ и т.д.

Плотность частоты (частости) представляет собой частоту, приходящуюся на единицу интервала, т.е. или , где h_i – величина интервала. Данный показатель используют, если интервалы вариационного ряда неравные и нужно рассчитать моду.

Теперь остановимся на показателях центра распределения и показателях степени вариации.

К показателям центра распределения относят среднюю, моду и медиану.

Средняя величина характеризует типичный уровень признака в совокупности. По данным вариационного ряда распределения средняя рассчитывается как арифметическая взвешенная.

Мода – значение признака, наиболее часто встречающееся в исследуемой совокупности (в вариационном ряду). Во многих случаях это величина наиболее характерна для ряда распределения и вокруг нее концентрируется большая часть вариантов.

Для дискретного ряда мода находится непосредственно по определению, по максимальной частоте или частности.

Для интервального ряда с равными интервалами сначала определяется модальный интервал, которому соответствует максимальная частота. Значение моды внутри модального интервала определяется по формуле:

, (5.6)

где x_о – нижняя граница модального интервала;

i - длина модального интервала;

f_{Мо – 1}, f_Мо, f_Мо+1 - частота (частности) модального, предмодального и послемодального интервала.

Медианой – называют такое значение признака, которое приходится на середину ранжированного (упорядоченного) ряда. Таким образом, это вариант, который делит ряд распределения на две равные по объему части.

Медиана, как и мода, не зависит от крайних значений вариантов, поэтому применяется для характеристики центра в ряду распределения с неопределенными границами. Для определения медианы в ранжированном ряду необходимо в начале найти номер медианы: ; затем используют кумулятивные частоты S_i или частность S_d.

В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.

Рассмотрим пример: в таблице исходя из наибольшего значения частоты определяем, что типичное число членов домашних хозяйств (самое распространенное значение) – 2 человека. Из 1000 домашних хозяйств 262 состоят всего из 2 человек (262 – максимальная частота ряда, а 2 – значение признака, которое встречается чаще всего, оно и является значением моды).

Таблица 4.1