1. Общее быстродействие  O(n^2).

2. Сортировка происходит на месте.

3. Неустойчивая.

4. Поведение неестественное.

 Сортировка вставками не относится к категории быстродействующих, поскольку единственный вид операции обмена, который она использует, выполняется над двумя соседними элементами, в связи с чем элемент может передвигаться вдоль массива лишь на одно место за один раз. Например, если наибольший элемент оказывается в конце массива, потребуется сделать N шагов, чтобы поместить его в надлежащее место. Сортировка методом Шелла представляет собой простейшее расширение метода вставок, быстродействие которого выше за счет обеспечения возможности обмена местами элементов, которые находятся далеко один от другого (элементы перемещаются большими скачками).

 

Идея метода:

В исходном массиве выделяю группы элементов. Каждая группа сортируется методом вставки. По ходу работы алгоритма размеры таких групп увеличиваются, пока все элементы массива не войдут в одну группу. Группой массива называется последовательность элементов, номера которых образуют арифметическую прогрессию с разностью h, которая называется шагом группы.

Основной вопрос - это выбор последовательности шагов. Существует достаточное количество исследований этого вопроса, и предложено большое количество методик выбора этой последовательности для разного числа элементов. Самый простой способ: h = n/2-1.

 Один из способов реализации сортировки методом Шелла заключается в том, что для каждой выделенной группы элементов независимо используется сортировка вставками на каждом из h подмассивов. Несмотря на очевидную простоту этого процесса, возможен еще более простой подход именно благодаря тому, что подмассивы независимы. В процессе h-сортировки массива мы просто вставляем элемент среди предшествующих ему элементов в соответствующем h-подмассиве, перемещая большие по значению элементы вправо. Эта задача решается путем использования программы сортировки вставками, при которой каждый шаг перемещения по массиву в сторону увеличения или уменьшения равен h, но не равен 1. С учетом данного обстоятельства программная реализация сортировки методом Шелла сводится всего лишь к тому, что для каждого значения шага осуществляется проход по массиву, характерный для сортировки вставками.

Пример

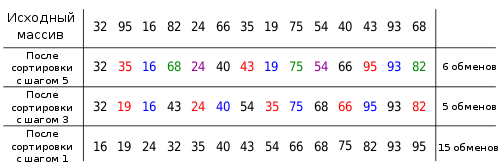
Пусть дан список и выполняется его сортировка методом Шелла, а в качестве значений (шага) выбраны .

На первом шаге сортируются подсписки , составленные из всех элементов , различающихся на 5 позиций, то есть подсписки , , , , .

В полученном списке на втором шаге вновь сортируются подсписки из отстоящих на 3 позиции элементов.

Процесс завершается обычной сортировкой вставками получившегося списка.

 Пирамидальная сортировка

 Общее быстродействие O(n*log(n)). Быстрая сортировка.

1. Сортировка на месте.

2. Неустойчивая.

3. Поведение неестественное.

Назовем пирамидой бинарное дерево высотой k, в котором все узлы имеют максимальный уровень k или k-1, то есть дерево является сбалансированным. При этом уровень k-1 заполнен полностью, а уровень k заполнен слева направо. 

Для пирамиды выполняется свойство: каждый элемент меньше либо равен родителю. Самым простым способом хранения пирамиды является массив. Соответствие между графическим представлением пирамиды и массивом осуществляется по правилам: в a[0] помещается корень дерева. Левый и правый сыновья элемента a[i]-го хранятся в ячейках, a[2*i+1] и a[2*i+2]. Таким образом, для массива, хранящего в себе пирамиду, выполняется свойство, что a[i]>=a[2*i+1] и a[i]>=a[2*i+2].

  Такой способ хранения имеет следующие преимущества:

• Для организации не используется дополнительная память.

• Узлы хранятся от вершины и далее вниз уровень за уровнем. Узлы одного уровня хранятся в массиве слева направо.

Чтобы воспользоваться пирамидальной сортировкой, необходимо выполнить 2 действия:

• по исходному массиву построить пирамиду,

• произвести сортировку.

 

Построение пирамиды

 Возьмем исходный массив.

44_55_12_42_94_18_06_67

 Построение пирамиды начнется с элементов a[k] и a[n], где n - количество элементов в массиве, а k =n/2, так как эта часть массива удовлетворяет свойству пирамиды (родитель больше или равен ребенку) по той причине, что эти элементы просто не имеют детей.

Далее будем расширять часть массива, обладающую свойством пирамиды. Для этого используется следующая процедура:

• начинаем двигаться от элемента k-1 до 0,

• смотрим на сыновей i-го элемента и выбираем наибольшего из них,

• если выбранный элемент больше чем a[i], то меняем его с a[i] местами, после чего опять переходим к шагу 3, рассматривая новое положение a[i]-го в массиве.

Пример построения пирамиды приведен на рисунке 1. Закрашенные элементы показывают, что данный элемент удовлетворяет правилу пирамиды.

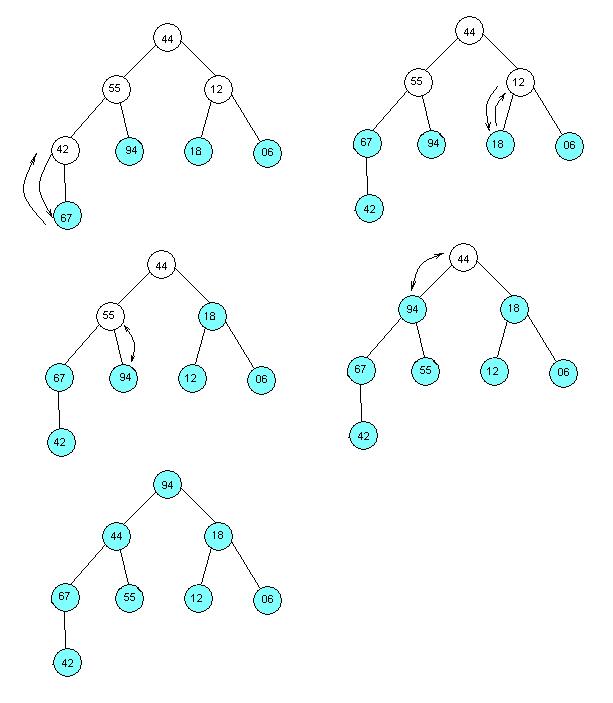
Рисунок 1. Построение пирамиды.

 

Сортировка

 Как видно из свойств пирамиды, в корне всегда находится максимальный элемент. Отсюда следует алгоритм:

• Берем максимальный элемент в корне и меняем его местами с последним неотсортированным элементом. После этого он находится на правильной позиции, и в дальнейшем алгоритме уже не участвует.

• Берем элемент, находящийся в вершине и для него выполняем алгоритм по построению пирамиды.

• Выполняем шаги 1 и 2, пока не останется неотсортированных элементов.

Поразрядная сортировка (RadixSort)

• Общее быстродействие O( n + m )

• Использует дополнительную память

• Устойчивая

• Не естественная

Поразрядная сортировка существенно отличается от описанных ранее.

Во-первых, он совсем не использует сравнений сортируемых элементов.

Во-вторых ключ, по которому идет сортировка разбивается на части (разряды). Например, при сортировке слов, слова можно разделить на буквы, при сортировке чисел, их можно поделить на цифры.

Для сортировки необходимо задать два дополнительных параметра:

k – количество разрядов в самом длинном ключе

m – разрядность данных (количество возможных значений для каждого разряда ключа).

Например, при сортировке русских слов m=33 (количество букв русского алфавита), k – количество букв в самом длинном слове.

При сортировке десятичных чисел m=10 (10 цифр от 0 до 9), k – максимальное количество цифр в числах участвующих в сортировке, для диапазона от 0 до 5000 k=4.

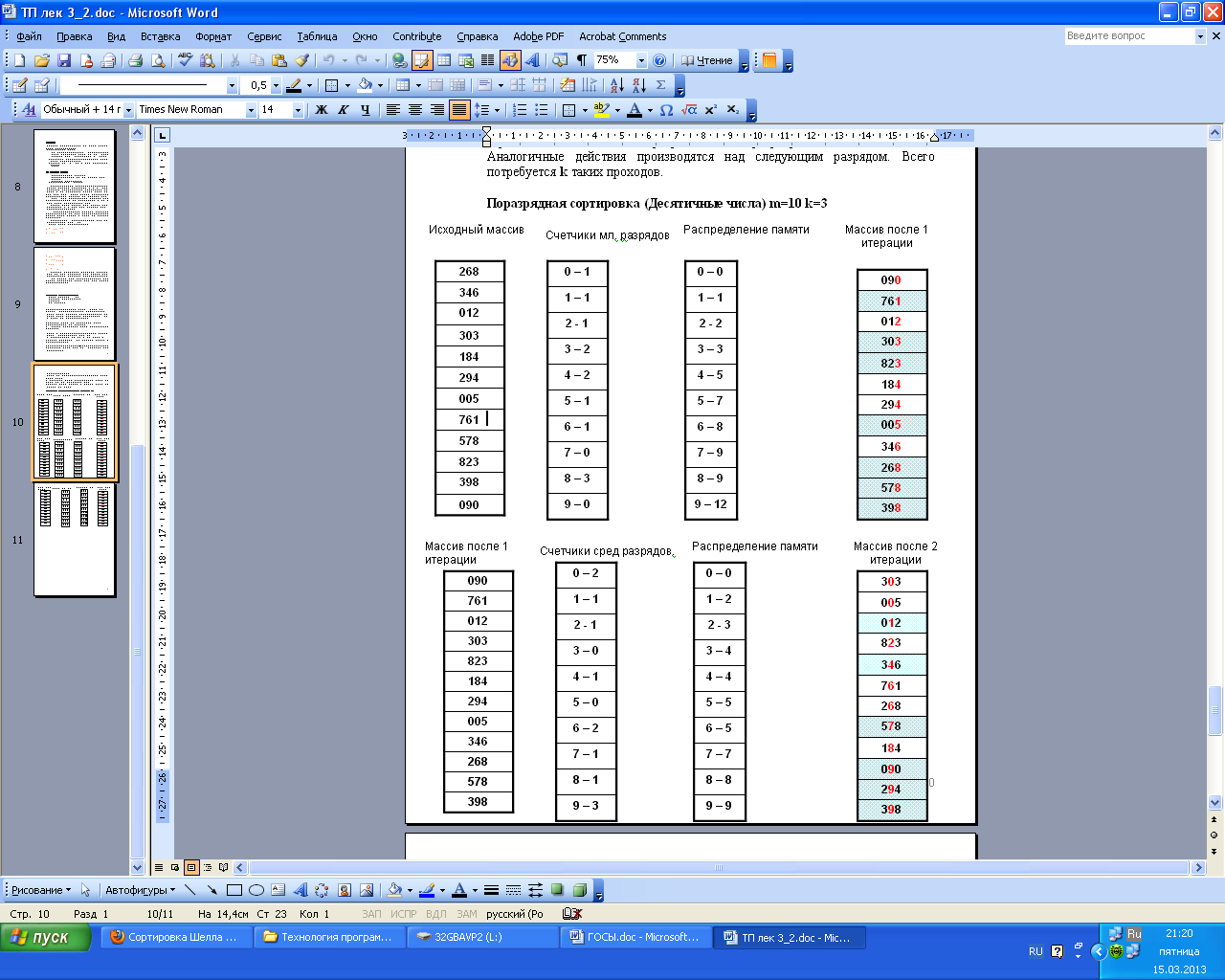
Основная идея заключается в выделении m счетчиков, которые ведут подсчет сколько чисел из исходного массива имеют в соответствующем разряде одинаковое значение.

Сортировка двухпроходная.

На первом этапе подсчитываются количество чисел имеющих, одинаковые значения в разряде.

На втором этапе на основании информации полученной на первом этапе строится новый массив, отсортированный по разряду.

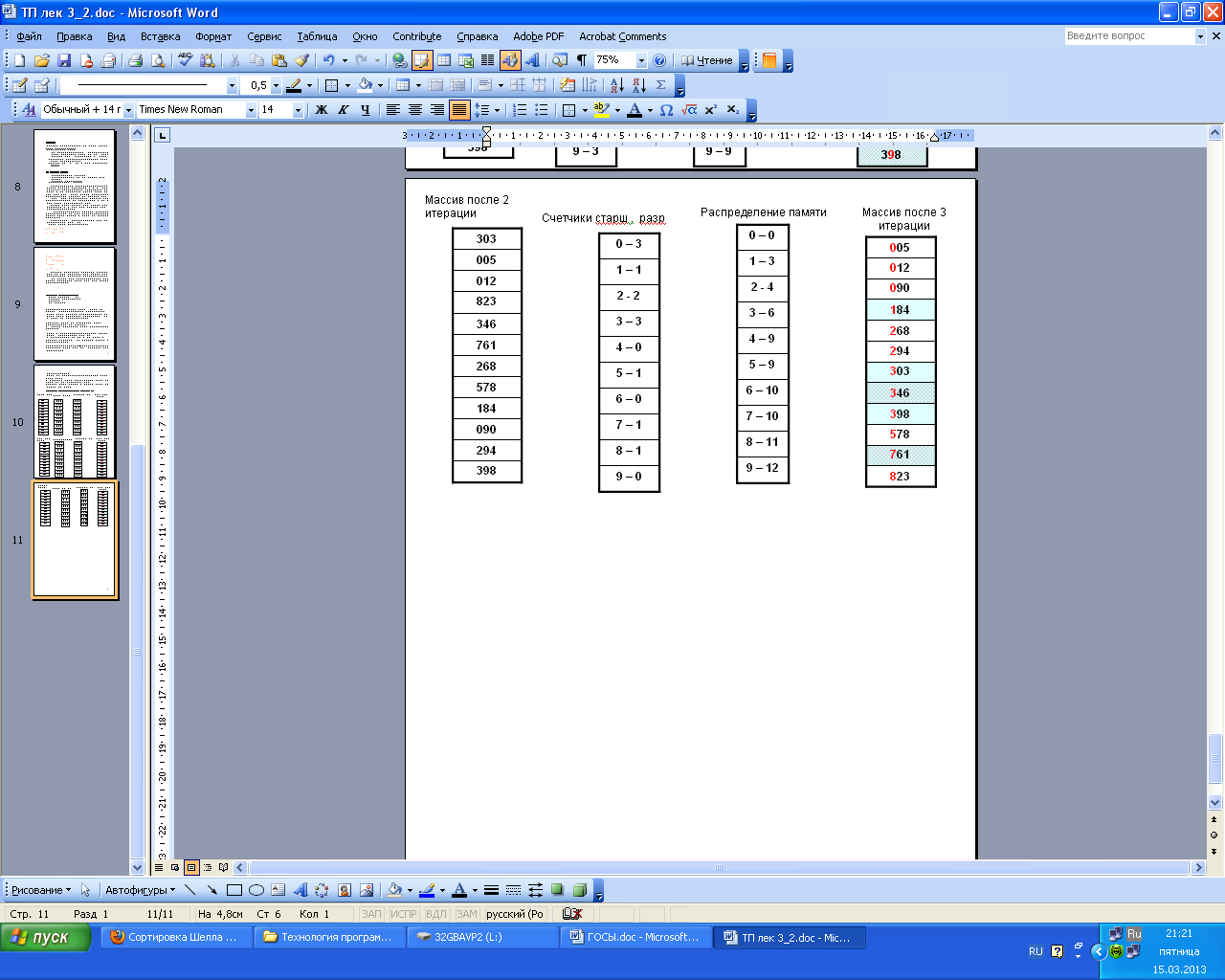
Аналогичные действия производятся над следующим разрядом. Всего потребуется k таких проходов.

Поразрядная сортировка (Десятичные числа) m=10 k=3

Сортировка подсчётом — алгоритм сортировки целых чисел в диапазоне от до некоторой константы или сложных объектов, работающий за линейное время.

Исходная последовательность из структур хранится в массиве , а отсортированная — в массиве того же размера. Кроме того, используется вспомогательный массив с индексами от до .

Идея алгоритма состоит в предварительном подсчете количества элементов с различными ключами в исходном массиве и разделении результирующего массива на части соответствующей длины (будем называть их блоками). Затем при повторном проходе исходного массива каждый его элемент копируется в специально отведенный его ключу блок, в первую свободную ячейку. Это осуществляется с помощью массива индексов , в котором хранятся индексы начала блоков для различных ключей. — индекс в результирующем массиве, соответствующий первому элементу блока для ключа .

• Пройдем по исходному массиву и запишем в 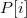количество структур, ключ которых равен .

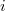• Мысленно разобьем массив на блоков, длина каждого из которых равна соответственно , , ..., .

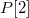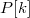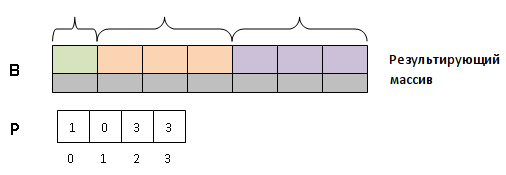
• Теперь массив нам больше не нужен. Превратим его в массив, хранящий в сумму элементов от до 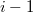старого массива .

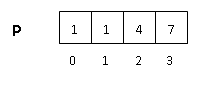
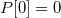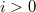
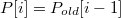• Теперь "сдвинем" массив на элемент вперед: в новом массиве , а для , где 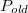— старый массив . Это можно сделать за один проход по массиву , причем одновременно с предыдущим шагом. После этого действия в массиве будут хранится индексы массива . указывает на начало блока в , соответствующего ключу .

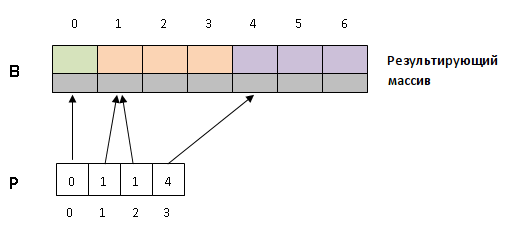
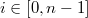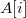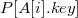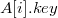• Произведем саму сортировку. Еще раз пройдем по исходному массиву и для всех будем помещать структуру в массив на место , а затем увеличивать на . Здесь — это ключ структуры, находящейся в массиве на -том месте.

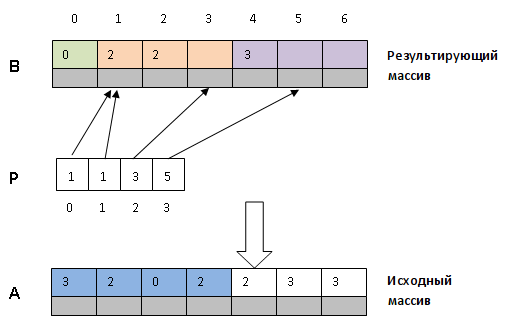
Таким образом после завершения алгоритма в будет содержаться исходная последовательность в отсортированном виде (так как блоки расположены по возрастанию соответствующих ключей).

Стоит также отметить, что эта сортировка является устойчивой, так как два элемента с одинаковыми ключами будут добавлены в том же порядке, в каком просматривались в исходном массиве . Благодаря этому свойству существует цифровая сортировка.