Технология программирования

7. Простейшие алгоритмы сортировки (пузырьковая, вставкой, выбором).

Пузырьковая сортировка

1. Общее быстродействие O(n^2), поэтому на практике практически не используется.

2. Дополнительные затраты на память. Сортировка происходит на месте.

3. Устойчивая.

4. Поведение неестественное.

Алгоритм работы сортировки:

1. При первом проходе по массиву элементы попарно сравниваются между собой: первый со вторым, затем второй с третьим и т.д. Если предшествующий элемент оказывается больше последующего, то их меняют местами.

2. Постепенно самое большое число оказывается последним. Остальная часть массива остается не отсортированной.

3. При втором проходе незачем сравнивать последний элемент с предпоследним. Последний элемент уже стоит на своем месте. Значит, число сравнений будет на одно меньше.

4. На третьем проходе уже не надо сравнивать предпоследний и третий элемент с конца. Поэтому число сравнений будет на два меньше, чем при первом проходе.

5. В конце концов, при проходе по массиву, когда остаются только два элемента, которые надо сравнить, выполняется только одно сравнение.

6. После этого первый элемент не с чем сравнивать, и, следовательно, последний проход по массиву не нужен. Другими словами, количество проходов по массиву равно m-1, где m – это количество элементов массива.

7. Количество сравнений в каждом проходе равно m-i, где i – это номер прохода по массиву (первый, второй, третий и т.д.).

8. При обмене элементов массива обычно используется "буферная" (третья) переменная, куда временно помещается значение одного из элементов.

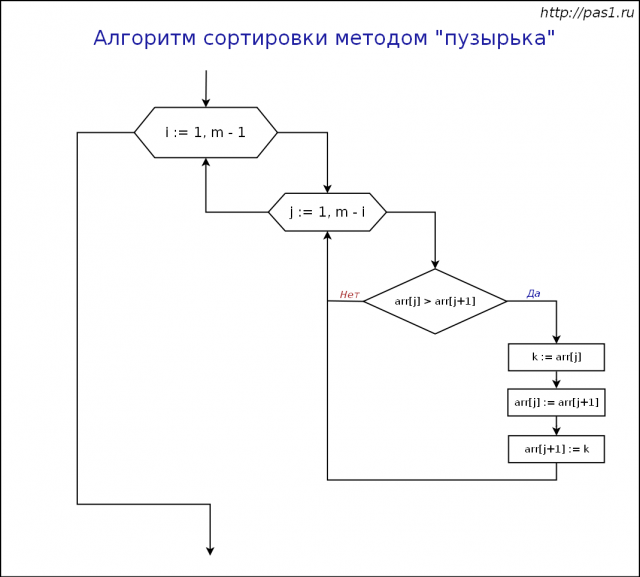
Сортировка выбором.

1. Общее быстродействие O(n^2).

2. Сортировка происходит на месте.

3. Неустойчивая.

4. Поведение неестественное.

Алгоритм сортировки:

1. Найти максимальный элемент (max) в массиве (arr).

2. Поместить его на последнее место (j).

3. Элемент, находившийся в конце массива переместить на место, где прежде находился max.

4. Уменьшить просматриваемую область массива на единицу (j – 1).

5. Снова найти максимальный элемент в оставшейся области.

6. Поместить его в конец просматриваемой области массива.

7. и т.д.

Сортировка вставками.

1. Общее быстродействие O(n^2). Но ввиду простоты реализации, является самой быстрой для малых массивов и списков (менее 20 элементов). В виду своих особенностей, алгоритм хорош для частично отсортированных данных.

2. Сортировка происходит на месте.

3. Устойчивая.

4. Поведение естественное.

Идея метода:

Сортируемый массив можно разделить на две части — отсортированная часть и неотсортированная. В начале сортировки первый элемент массива считается отсортированным, все остальные — не отсортированные. Начиная со второго элемента массива и заканчивая последним, алгоритм вставляет неотсортированный элемент массива в нужную позицию в отсортированной части массива. Таким образом, за один шаг сортировки отсортированная часть массива увеличивается на один элемент, а неотсортированная часть массива уменьшается на один элемент.

Рассмотрим пример сортировки по возрастанию массива из 7 чисел (см. Таблица 1): исходный массив: 3 3 7 1 2 5 0

Таблица 1 — Сортировка вставками
шаг	отсортированная часть массива							тек. элемент	вставка
1	3							3	false
2	3	3						7	false
3	3	3	7					1	true
4	1	3	3	7				2	true
5	1	2	3	3	7			5	true
6	1	2	3	3	5	7		0	true
-	0	1	2	3	3	5	7	-	-

На каждом шаге сортировки сравнивается текущий элемент со всеми элементами в отсортированной части. На первом шаге сравнивается тройка с тройкой, они равны поэтому не меняем их местами. На втором шаге сравниваем 7 с двумя тройками, 7 > 3 а так как сортировка по возрастанию, то опять элементы массива остаются на своих местах. На третьем шаге единица сравнивается с тремя элементами и все они больше единицы, значит единицу вставляем на первое место, в начало массива. На четвёртом шаге текущий элемент — 2 сравниваем с элементами 1, 3, 3, 7. Получается, что  1 < 2 < 3 и 7 поэтому двойку вставляем между единицей и тройкой. Пятый и шестой шаги выполняются точно также. В итоге на шестом шагу мы получаем отсортированный по возрастанию массив.