МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
АЛМАТИНСКИЙ КОЛЛЕДЖ СВЯЗИ
ПРИ КАЗАХСКО – АМЕРИКАНСКОМ УНИВЕРСИТЕТЕ
Тыщенко Е.М.
Сборник активного раздаточного материала
по курсу «Теория электрических цепей - 2».
для студентов специальностей:
130609 3 – Радиоэлектроника и связь,
130904 3 – Оптическое и электронное оборудование
Алматы 2011 г.
Автор: Тыщенко Е.М., преподаватель второй категории АКС при КАУ.
Рекомендовано к изданию решением Научно – Методического Совета КАУ, протокол № ____ дата ______________ 2011 г.
В сборнике представлен конспект лекций по дисциплине «Теория электрических цепей – 2»
Ó Казахско-Американский Университет
Список сокращений
АЧХ- амплитудно-частотная характеристика
ФЧХ- фазо-частотная характеристика
ФНЧ- фильтр нижних частот
ФВЧ- фильтр верхних частот
ПФ- полосовой фильтр
ЗФ- заграждающий (режекторный) фильтр
СРСП- самостоятельная работа студента с преподавателем
СРС- самостоятельная работа студента
ПП-полоса пропускания
ПЗ- полоса запирания
КЛ- колебательный контур
Нп- Непер
дБ- децибел
ЭДС- электродвижущая сила
Лекция 1 Последовательный колебательный контур. Резонанс напряжений. Условия и признаки
Резонанс – это явление в электрической цепи, содержащей участки, имеющие индуктивный и емкостной характер, при котором сдвиг фаз между током и напряжением на входе равен 0.
Вывод:
1. Условие наступления режима резонанса напряжений:
равенство
частоты источника частоте собственных
колебаний контура
равенство
реактивных сопротивлений контура
,
полное реактивное сопротивление равно
0.
2. Признаки резонанса напряжений
Напряжение
на индуктивности равно напряжению на
емкости на емкости и превышает напряжение
на входе в
раз.
Цепь
имеет чисто резистивный (активный)
характер,
и имеет минимальное занчение.
Ток
в цепи максимален и равен
Сдвиг фаз между входным током и входным напряжением равен 0.
Характеристическое (волновое) сопротивление
Величина
любого из реактивных сопротивлений при
резонансе равна волновому
(характеристическому) сопротивлению
контура.
.
В
радиотехнических колебательных контурах
во много раз превышает
.
Вот почему напряжение на емкости и
индуктивности во много раз превышают
напряжение на входе.
Добротность конура
Отношение
волнового сопротивления к активному,
определяющее коэффициент повышения
напряжения на реактивных сопротивлениях
по отношению к поданному на контур
напряжению, называется добротностью.
.
Величина,
обратная добротности, называется
затуханием
.
Если
колебательный контур отключить от
внешнего источника, и он будет замкнут
накоротко, то колебательный процесс
затухает интенсивнее, чем больше
.
Вывод:
Резонанс в последовательном контуре называют резонансом напряжений, т.к. напряжение на индуктивности равно напряжению на емкости и в раз больше напряжения на входе.
,
ток в контуре при резонансе
Добротность нагруженного контура
При
использовании колебательных контуров
в радиотехнических устройствах к одному
из реактивных элементов подключается
нагрузка, обладающая определенным
сопротивлением. Это сопротивление
принято называть вносимым и обозначать
.
Это приводит к увеличению потерь в цепи
и уменьшению добротности.
Данную
цепь можно заменить эквивалентной с
последовательным соединением
,
тогда схема примет вид
Понятие расстройки
При работе с колебательными контурами важно знать совпадает ли частота генератора с резонансной частотой. Если частота генератора равна резонансной, то говорят, что контур настроен на частоту источника. А, если частота генератора отличается от резонансной частоты контура, то расстроен. Введем понятие расстроек
Абсолютная расстройка:
.
Абсолютные расстройки могут быть как
положительными, так и отрицательными.Относительная расстройка
Обобщенная расстройка- это отношение сопротивлений всех реактивных элементов контура к резистивному сопротивлению
.
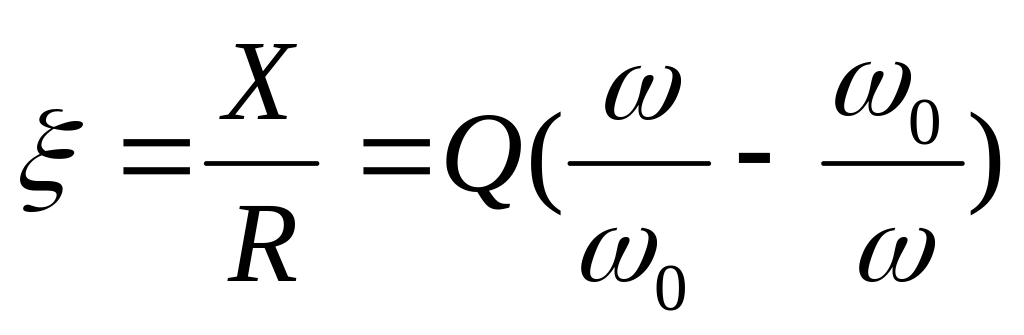Вывод:
При резонансе все расстройки равны 0.
При
,
расстройки отрицательны.
При
,растройки
положительны.
Обобщенная растройка характеризует удаленность от резонансной частоты
Использование обобщенной расстройки значительно упрощает уравнения и облегчает расчет характеристик.