2.2. Однокритериальные задачи принятия решений

Детерминированные и неопределенные задачи принятия решений можно считать предельными случаями вероятностных задач. В силу этого рассмотрим сначала вероятностные задачи, а затем детерминированные и неопределенные.

Для описания вероятностных задач удобно использовать матрицы, в которых каждый столбец определяет возможный результат, а каждая строка – возможную стратегию.

Элементы u_ij матрицы определяют полезности результатов O_j при стратегиях c_i, т.е.

а элементы p_ij – вероятности получения результатов O_j при стратегиях c_i, т.е.

Матрица такого вида называется платежной матрицей.

Для использования основных критериев (в частности критерия максимума математического ожидания полезности) результаты следует задавать так, чтобы они образовывали полную группу несовместных событий. Если это условие не выполняется, то, используя булево разложение, можно получить составные результаты, удовлетворяющие указанному требованию. Так, например, если имеется два результата Q₁ и Q₂, не образующие полной группы несовместных событий, то можно образовать четыре составных результата, обладающих этим свойством:

O₁: имеют место Q₁ и Q₂;

O₂: имеет место Q₁, но не Q₂ (Q₁ и );

O₃: имеет место Q₂, но не Q₁ ( и Q₂);

O₄: не имеют места ни Q₁, ни Q₂ ( и ).

Математическое ожидание полезности i-й стратегии определяется следующим образом:

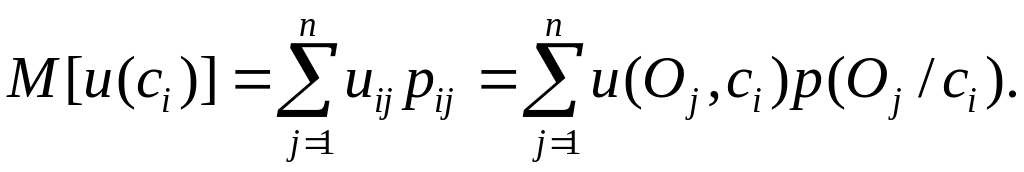
В большинстве вероятностных задач для выбора стратегии обычно применяется критерий максимума математического ожидания полезности. Согласно этому критерию необходимо выбрать такую стратегию c^*, которая обеспечивает максимум M^* математического ожидания полезности, т.е.

Чаще всего эта задача решается простым перебором значений для всех c_i (особенно, если число n строк платежной матрицы невелико).

Детерминированную задачу можно рассматривать как предельный случай вероятностной задачи, когда для каждой стратегии вероятность получения одного из возможных результатов равна 1, а вероятности получения остальных результатов равны 0.

Для выбора стратегии применяется критерий максимума полезности. Согласно этому критерию необходимо найти такую стратегию c^*, которая приводит к результату, имеющему максимальную полезность, т.е.

где при

Одним из определяющих факторов в неопределенных задачах является внешняя среда (природа), которая может находиться в одном из состояний θ_l, с вероятностью p(θ_l). В зависимости от состояния θ_l среды результат O_j реализации стратегии c_i достигается с вероятностью , т.е. каждому результату при фиксированной стратегии соответствует не одна, как ранее, а L вероятностей.

Математическое ожидание полезности i-й стратегии в данном случае определяется следующим образом:

,

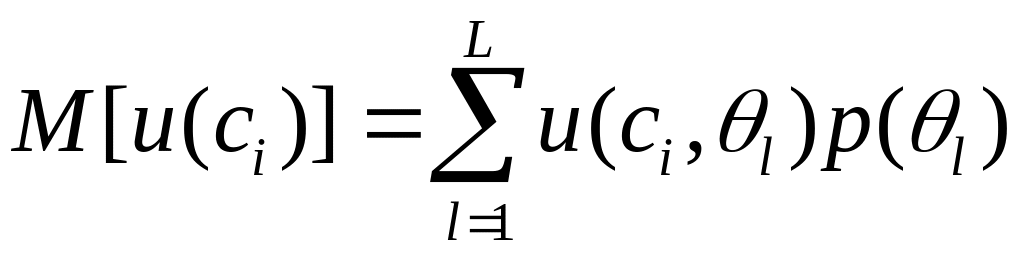где − математическое ожидание полезности i-й стратегии при l-м состоянии внешней среды.

Платежная матрица в данном случае имеет размер m×L, каждый столбец матрицы определяет возможное состояние внешней среды, каждая строка – возможную стратегию.

	θl ci	θ1	θ2	…	θL
	c1	u11	u12	∙∙∙	u1L
U =	c2	u21	u22	∙∙∙	u2L
	∙∙∙	∙∙∙	∙∙∙	∙∙∙	∙∙∙
	cm	um1	um2	∙∙∙	umL

Элементы u_il матрицы определяют полезность, обеспечиваемую стратегией c_i при состоянии среды θ_l,т.е.

Проблема выбора оптимальной стратегии заключается в том, что вероятности P(θ_l), не известны ЛПР. Для выбора оптимальной стратегии используются несколько критериев.

Методика применения указанных критериев заключается в следующем:

1. Определяют (тем или иным способом) некоторую меру эффективности для каждой стратегии

2. Выбирают такую стратегию c^*, которая обеспечивает экстремальное значение меры эффективности w^*=w(c^*).

Критерий Вальда (критерий осторожного наблюдателя). В соответствии с данным критерием выбирается стратегия, максимизирующая полезность в случае, когда среда находится в наихудшем для ЛПР состоянии. Таким образом,

Поскольку

то данный критерий является критерием максимина.

Критерий Лапласа. В соответствии с данным критерием выбирается стратегия, максимизирующая полезность в случае, когда все состояния среды считаются равновероятными, т.е. p(θ_l)=1/L, Таким образом,

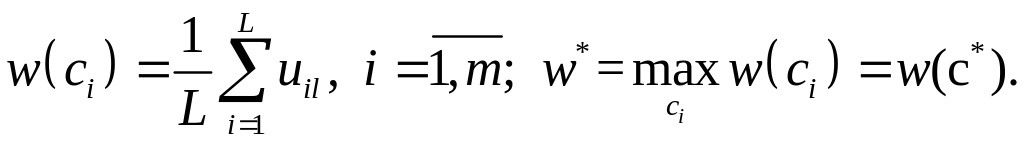
Критерий Гурвица (обобщенный максимин). В соответствии с данным критерием выбирается стратегия, максимизирующая полезность при условии, что среда может находиться в наилучшем состоянии с вероятностью α и в наихудшем состоянии с вероятностью 1-α; очевидно, что . Таким образом,

Критерий Сэвиджа. Чтобы использовать этот критерий, платежную матрицу U необходимо преобразовать в матрицу потерь V. В каждую клетку матрицы потерь записывается разность между максимальным значением полезности при данном состоянии среды и тем значением полезности, которое записано в соответствующей клетке платежной матрицы. Таким образом, элементы v_il матрицы потерь определяются из соотношений

В соответствии с критерием Сэвиджа выбирается стратегия, минимизирующая возможные потери при условии, что среда находится в наихудшем для ЛПР состоянии. Таким образом,

Поскольку

то данный критерий является критерием минимакса.

Задачи

2.4. Рассматривается два результата:

Q₁ – выпадение 1 при бросании игральной кости,

Q₂ – выпадение 2 при бросании игральной кости.

Сформировать четыре составных результата O₁÷O₄, образующих полную группу несовместных событий, и найти вероятности их получения.

2.5. По объекту противника ведется стрельба. При этом возможны следующие результаты:

1) отсутствие поражения (промах) – ущерб противнику 0 д.е.,

2) незначительное повреждение – ущерб противнику 10 д.е.,

3) значительное повреждение – ущерб противнику 30 д.е.,

4) полное уничтожение – ущерб противнику 60 д.е.

В зависимости от количества израсходованных боеприпасов затраты составляют:

1) малое количество боеприпасов – затраты 10 д.е.,

2) среднее количество боеприпасов – затраты 20 д.е.,

3) большое количество боеприпасов – затраты 40 д.е.

Определить оптимальное количество израсходованных боеприпасов для следующих вероятностей получения результатов: p₁₁=0,3; p₁₂=0,4; p₁₃=0,2; p₁₄=0,1; p₂₁=0,15; p₂₂=0,25; p₂₃=0,35; p₂₄=0,25; p₃₁=0,05; p₃₂=0,1; p₃₃=0,25; p₃₄=0,6.

2.6. Швейная фабрика может изготовить партию пальто. Затраты на изготовление составляют: 20 пальто – 30 д.е., 40 пальто – 58 д.е., 60 пальто – 86 д.е., 80 пальто – 113 д.е.

Доход в зависимости от количества проданных пальто составляет: 20 пальто – 40 д.е., 40 пальто – 80 д.е., 60 пальто – 120 д.е., 80 пальто – 160 д.е.

Определить оптимальное количество изготавливаемых пальто. Найти решение задачи, применив критерии Лапласа, Гурвица (α=0,8).

2.7. Продавец заказывает газеты по цене 0,5 д.е. за газету и продает по цене 1 д.е. Непроданные газеты он возвращает по цене 0,2 д.е. за газету. Продавец знает, что спрос не превышает 50 газет. Определить оптимальное количество заказываемых газет (размер заказа должен быть кратен 10, т.е. продавец может заказать 10, 20, 30, 40 или 50 газет).

Найти решение задачи, применив критерии Вальда, Лапласа, Гурвица (α=0,5) и Сэвиджа.

2.8. Найти решение задачи 2.7 с учетом того, что наблюдение за спросом на газеты в течение 100 дней дало следующие результаты:

Спрос на газеты	0	10	20	30	40	50
Число дней	3	17	37	29	12	2