1.5. Транспортная задача

Постановка транспортной задачи формулируется следующим образом.

В пунктах производства А₁, А₂,…, А_m имеются запасы некоторого однородного продукта в количествах а₁, а₂,…, а_m единиц. Данный продукт потребляют в пунктах В₁, В₂,…, В_n в количествах b₁, b₂,…, b_n единиц. Из каждого пункта производства возможна транспортировка продукта в любой пункт потребления. Транспортные издержки на перевозку единицы продукции из пункта А_i в пункт В_j составляют

Требуется составить такой план перевозок, при котором весь продукт из пунктов производства вывезен, запросы всех потребителей удовлетворены и суммарные транспортные издержки минимальны.

Пусть x_ij – количество продукта, перевозимого из пункта А_i в пункт В_j, Тогда математическая модель транспортной задачи имеет следующий вид:

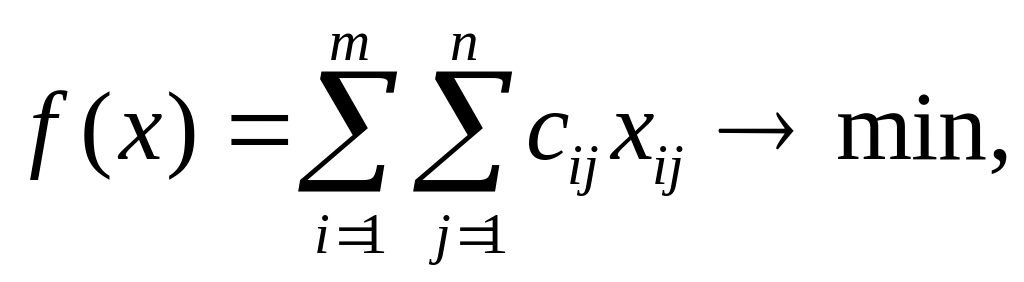(1.26)

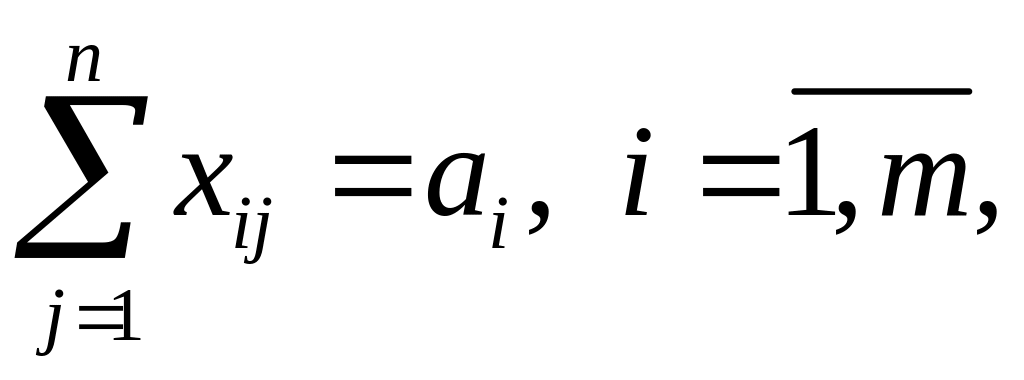(1.27)

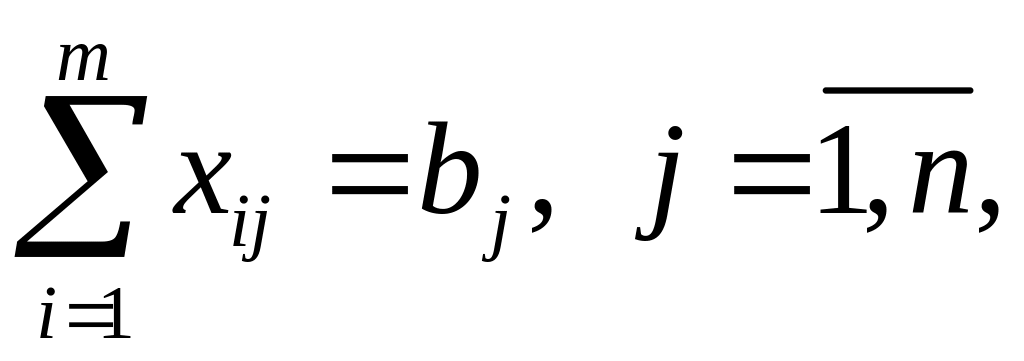(1.28)

(1.29)

Условие (1.27) означает полный вывоз продукта из всех пунктов производства, а условие (1.28) − полное удовлетворение спроса во всех пунктах потребления.

Набор переменных x_ij, удовлетворяющий условиям (1.27)÷(1.29), записывают в виде матрицы

Матрицу Х называют планом перевозок транспортной задачи, а переменные х_ij − перевозками. План X*, при котором целевая функция минимальна, называется оптимальным планом.

Необходимым и достаточным условием разрешимости транспортной задачи является условие баланса

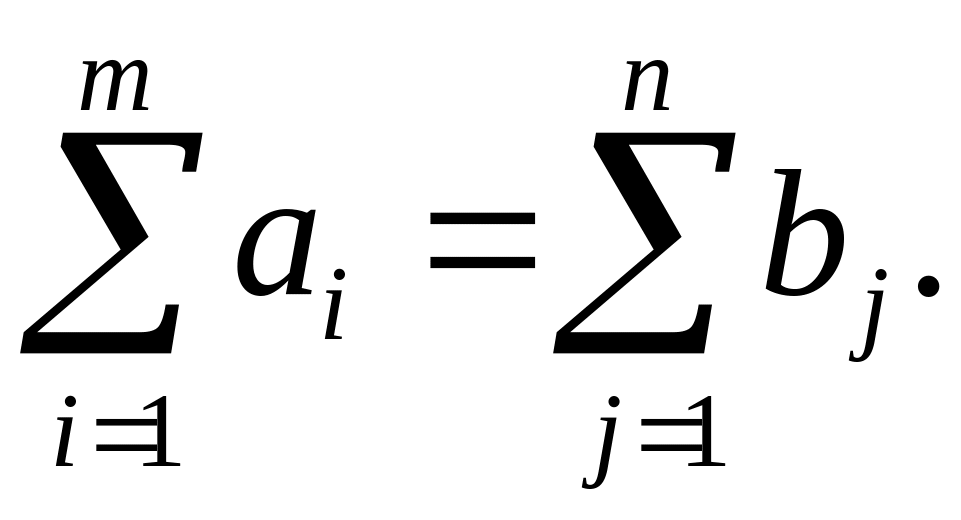(1.30)

Это условие означает, что объем производства (предложение) должен быть равен объему потребления (спроса).

Модель (1.26)÷(1.29) транспортной задачи при выполнении условия (1.30) называется закрытой моделью, а при не выполнении условия (1.30) − открытой моделью.

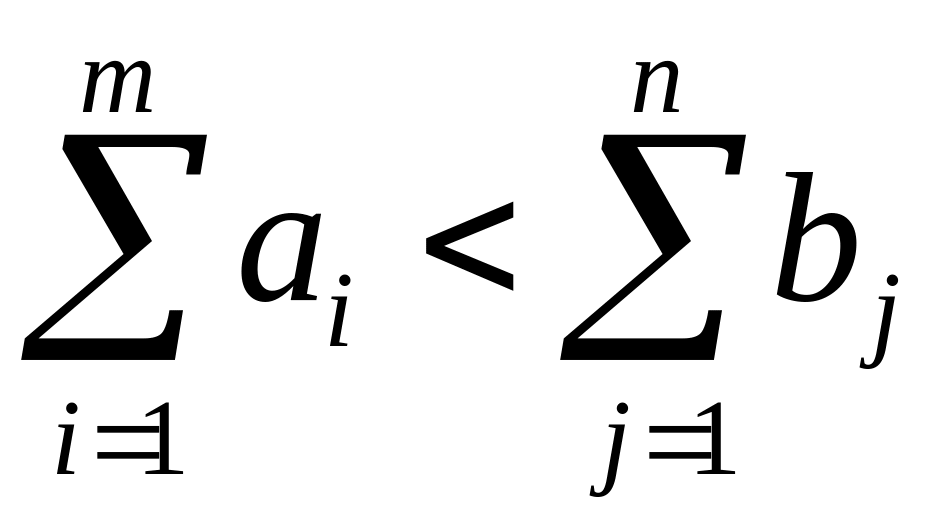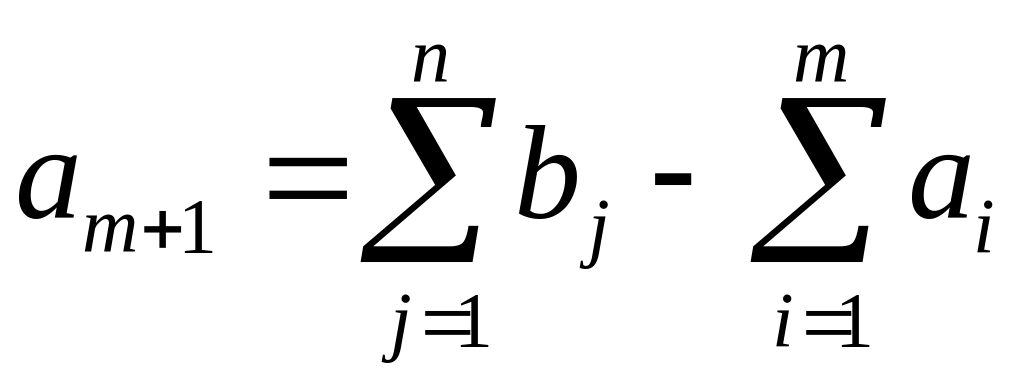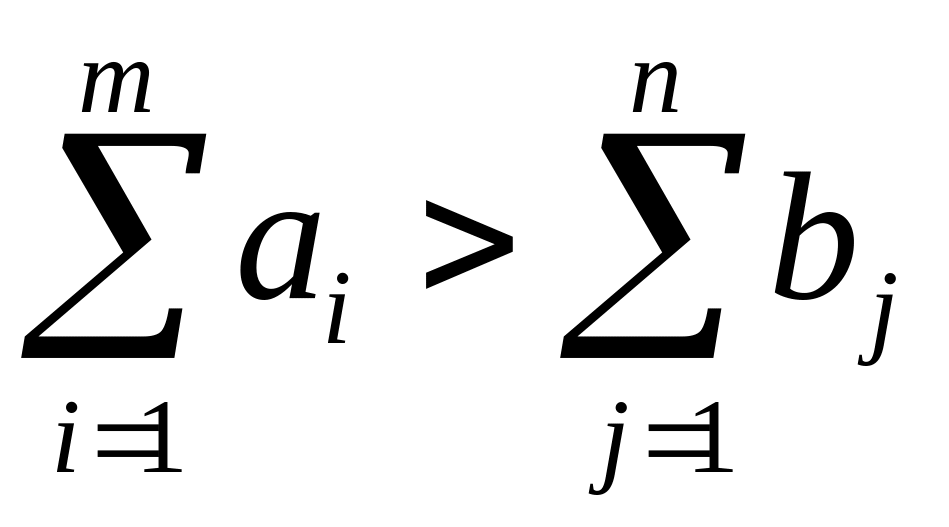Для своего решения задача, описываемая открытой моделью, должна быть сведена к задаче, описываемой закрытой моделью. При необходимо ввести фиктивный пункт производства A_m+1 с объемом производства и транспортными издержками (в оптимальном решении Х* полагают ). При необходимо ввести фиктивный пункт потребления B_n+1 с объемом потребления 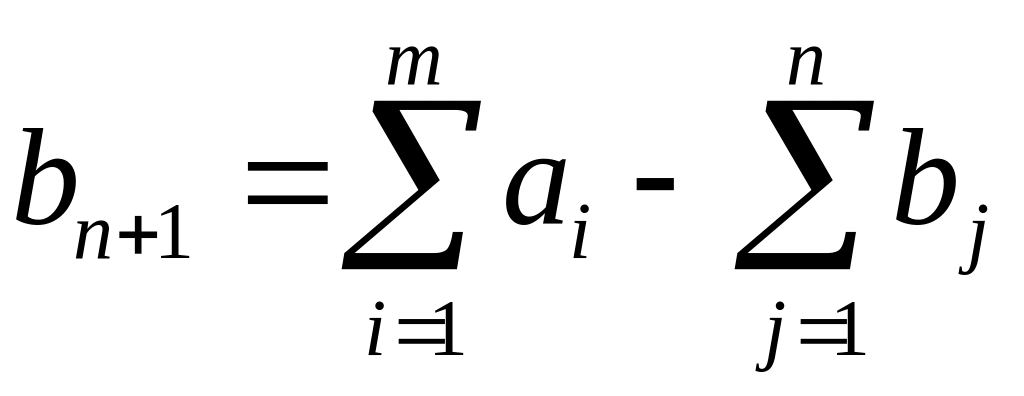и транспортными издержками (в оптимальном решении Х* полагают ).

Число переменных х_ij в транспортной задаче с m пунктами производства и n пунктами потребления равно nm, а число уравнений в системах (1.27) и (1.28) равно n+m. Так как предполагается, что выполняется условие баланса (1.30), то число линейно независимых уравнений равно n+m−1. Следовательно, ранг системы ограничений (1.27)÷(1.28) и число базисных переменных равно n+m−1. Для транспортных задач вместо понятия «допустимое базисное решение» используется эквивалентное ему понятие «опорный план». Таким образом, опорный план транспортной задачи может иметь не более n+m−1 отличных от нуля компонент.

Существуют различные методы решения транспортной задачи. На практическом занятии рассматривается метод потенциалов. Алгоритм метода потенциалов состоит из предварительного этапа и конечного числа итераций. На предварительном этапе строится начальный опорный план Х₀, а затем осуществляется его улучшение до тех пор, пока не будет выполняться условие оптимальности плана.

Для определения начального опорного плана разработаны несколько методов. Два из них – метод северо-западного угла и метод минимального элемента − рассматриваются на практическом занятии.

В случае метода северо-западного угла для определения начального опорного плана Х₀ используются только вектор производства и вектор потребления . Заполнение таблицы для Х₀ начинается с левого верхнего элемента х₁₁, что и обусловило название − метод северо-западного угла.

Процедура заполнения таблицы Х₀ состоит из n+m−1 шагов (на каждом шаге определяется одна базисная переменная). На k-м, k=1,2,…,n+m−1, шаге выполняют следующие действия:

1. Определяют левый верхний элемент , причем незаполненной части таблицы

где − соответственно векторы производства и потребления, полученные на (k−1)-м шаге (первоначально полагают ).

При этом возможны 2 случая:

− если , то все незаполненные позиции ν-й строки (позиции свободных переменных) заполняют нулями;

− если , то все незаполненные позиции μ-го столбца (позиции свободных переменных) заполняют нулями.

2. Определяют новые вектор производства и вектор потребления по правилам:

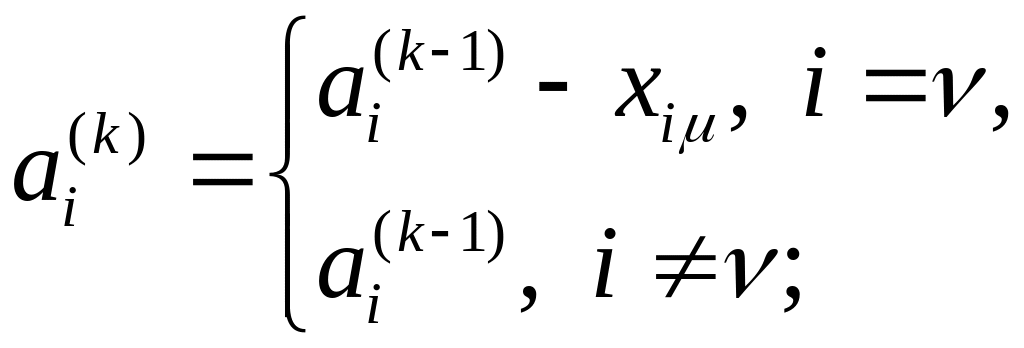
(1.31)

Таким образом, как следует из соотношений (1.31), изменяются только ν-й элемент вектора и μ-й элемент вектора .

При определении начального опорного плана Х₀ строят таблицу размера m×n. Для удобства вычислений справа к таблице приписывают n+m m-разрядных столбцов, в которые записывают вектора производства , а снизу к таблице приписывают n+m n-разрядных строк, в которые записывают вектора потребления .

		1	2	∙∙∙	n	a(0)	a(1)	∙∙∙	a(n+m-1)
	1
	2
X0 =	∙∙∙
	m
	b(0)
	b(1)
	∙∙∙
	b(n+m-1)

Отметим, что вектора и должны быть нулевыми. Это условие может использоваться для проверки правильности вычислений.

В случае метода минимального элемента для определения начального опорного плана Х₀ используются как вектора производства , и потребления , так и матрица транспортных издержек План строится таким образом, чтобы перевозки х_ij выполнялись, по возможности, по маршрутам с минимальной стоимостью. Благодаря этому, данный метод позволяет получить более экономичный (по сравнению с методом северо-западного угла) начальный план, сокращая тем самым общее число итераций по его оптимизации.

Элементы матрицы С нумеруют, начиная с минимального, в порядке возрастания и в том же порядке нумеруют элементы матрицы Х₀. Заполнение матрицы Х₀ осуществляется по правилам метода северо-западного угла, но на каждом шаге в незаполненной части таблицы выбирается не левый верхний элемент, а элемент с минимальным порядковым номером.

Отметим, что после построения начального опорного плана нули в клетках матрицы, соответствующих свободным переменным, опускают, чтобы отличать эти клетки от клеток, содержащих нулевые базисные переменные. Таким образом, число заполненных клеток матрицы Х₀ равно n+m−1, остальные клетки – свободные.

Для проверки оптимальности текущего опорного плана X используется оценочная матрица Z. Схема расчета Z заключается в следующем. Пунктам производства А_i , , и потребления В_j, , ставятся в соответствие числа u_i и v_j, называемые их потенциалами. Для каждой базисной переменной х_ij опорного плана потенциалы должны удовлетворять уравнению

(1.32)

Эти уравнения образуют систему, состоящую из n+m−1 уравнений, в которых фигурируют n+m неизвестных. Значения потенциалов можно определить из этой системы, придавая одному из них произвольное значение (обычно полагают u₁=0).

Элементы z_ij оценочной матрицы определяются из соотношений

(1.33)

Очевидно, что элементы z_ij, соответствующие базисным переменным x_ij, будут равны нулю.

Если оценочная матрица не содержит положительных элементов, т.е. то текущий опорный план является оптимальным. В противном случае определяют новый опорный план. При этом одна из свободных переменных вводится в текущий базис, а одна из базисных переменных из него исключается.

Для включения в базис выбирается свободная переменная x_pq , которой соответствует максимальный положительный элемент z_pq оценочной матрицы Z. Для определения исключаемой переменной в таблице Х строят замкнутый цикл, который начинается и заканчивается выбранной свободной переменной. Цикл состоит из последовательности горизонтальных и вертикальных (связанных) отрезков, концами которых должны быть базисные переменные. Это означает, что каждая вершина цикла должна содержать базисную переменную.

Из базиса выводится та базисная переменная x_rs, которая имеет минимальное значение θ среди всех нечетных по порядку расположения в цикле базисных переменных, считая первой следующую за x_pq базисную переменную.

Строится новый опорный план, прибавляя θ ко всем четным элементам цикла и вычитая из нечетных. Элементы текущей матрицы Х, не входящие в цикл, переносятся в следующую матрицу Х без изменения. Описанный переход от одного опорного плана транспортной задачи к другому называется сдвигом по циклу пересчета. Затем проверяют условие оптимальности полученного опорного плана.

Таким образом, алгоритм решения транспортной задачи методом потенциалов заключается в следующем:

1. Определяют начальный опорный план Х₀ (при этом число заполненных клеток должно быть равно n+m−1).

2. Используя соотношения (1.32), находят потенциалы u_i, , v_j, , соответственно пунктов производства и потребления.

3. Используя соотношения (1.33), вычисляют оценочную матрицу Z.

4. Проверяют условие оптимальности текущего опорного плана: оценочная матрица не содержит положительных элементов.

Если условие выполняется, то текущий опорный план является оптимальным опорным планом Х*.

Если условие не выполняется, то переходят к п. 5.

5. В базис вводят свободную переменную текущего опорного плана, которой соответствует максимальный положительный элемент текущей оценочной матрицы. Для вводимой переменной строят замкнутый цикл. Из базиса выводят базисную переменную, имеющую минимальное значение среди всех нечетных базисных переменных цикла.

6. Производят сдвиг по циклу пересчета и получают новый опорный план. Затем переходят к п.2.

Вычисления завершают, когда найден оптимальный опорный план Х* (п.4).

Задачи

1.11. Три предприятия для производства продукции получают сырье от четырех поставщиков. Потребности в сырье каждого из предприятий соответственно равны 160, 140 и 170 ед. Запасы сырья у поставщиков соответственно равны 120, 50, 190 и 110 ед. Тарифы перевозок единицы сырья от каждого из поставщиков каждому предприятию задаются матрицей

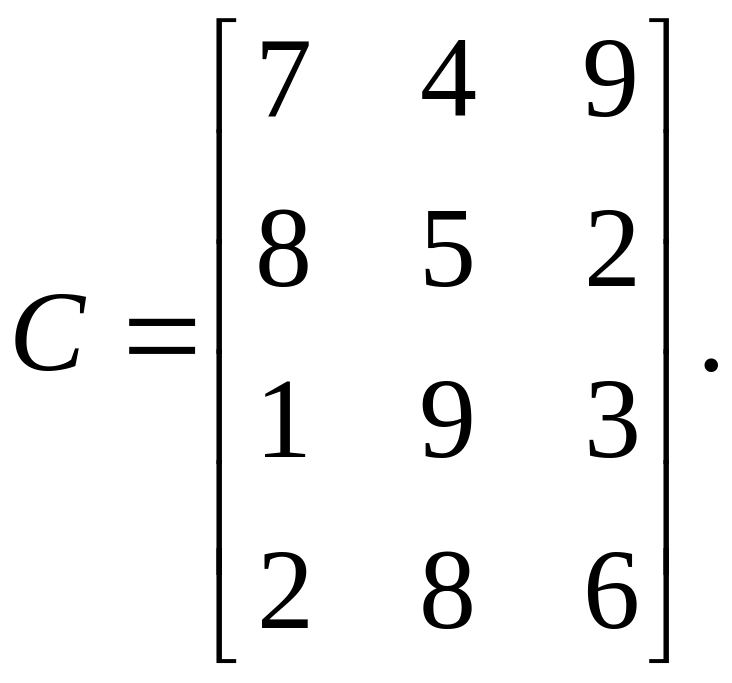
Найти начальный план перевозок данной транспортной задачи а) методом северо-западного угла, б) методом минимального элемента.

1.12. Три предприятия производят однородную продукцию соответственно в количествах 6, 8 и 10 ед. Эту продукцию следует перевезти в четыре магазина. Каждый из магазинов должен получить соответственно 4, 6, 8 и 6 ед. продукции. Тарифы перевозок единицы продукции от каждого из предприятий в каждый магазин задаются матрицей

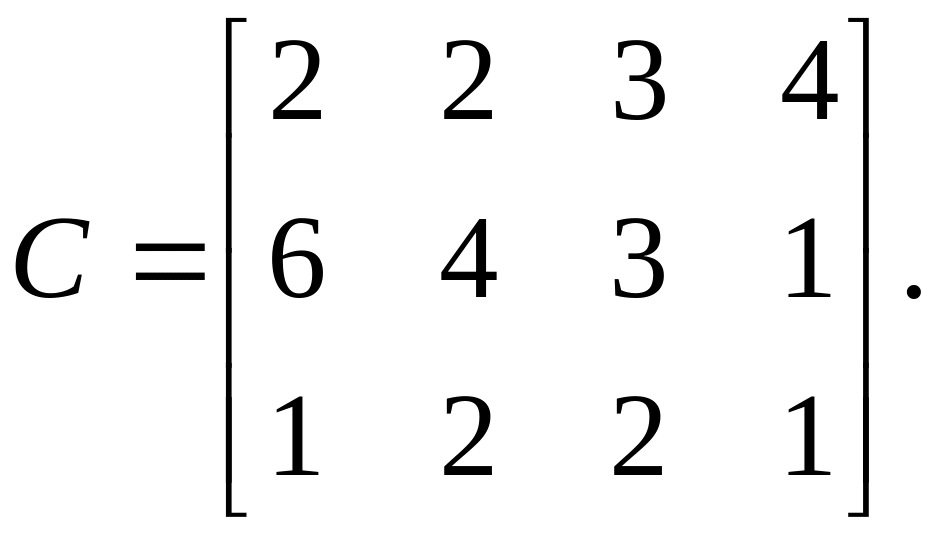
Найти такой план перевозок продукции, при котором суммарные транспортные издержки минимальны.

Решить данную транспортную задачу методом потенциалов, определив начальный опорный план а) методом северо-западного угла, б) методом минимального элемента.