1.3. Симплекс-метод решения задачи лп

Симплекс-метод требует приведения задачи ЛП к канонической форме, т.е. к виду (1.5) (1.7), причем все b_i в (1.6) должны быть неотрицательными, т.е. (если некоторое b_i<0, то соответствующее ограничение надо умножить на (−1)). Расчеты симплекс-методом наиболее удобно проводить с помощью симплекс-таблиц.

Для задачи ЛП вида (1.5) (1.7) симплекс-таблица состоит из n+2 столбцов и m+1 строк. В первых m строках симплекс-таблицы записываются коэффициенты уравнений, выражающих базисные переменные через свободные, в (m+1)-й строке (целевой строке) – коэффициенты уравнения , где – целевая функция, зависящая только от свободных переменных. Указанные уравнения преобразованы таким образом, что все переменные содержатся в одной части уравнений, а свободные члены – в другой части.

Так, если базисными являются переменные x_n-m+1 x_n, то уравнения, выражающие базисные переменные через свободные, и целевая функция имеют вид:

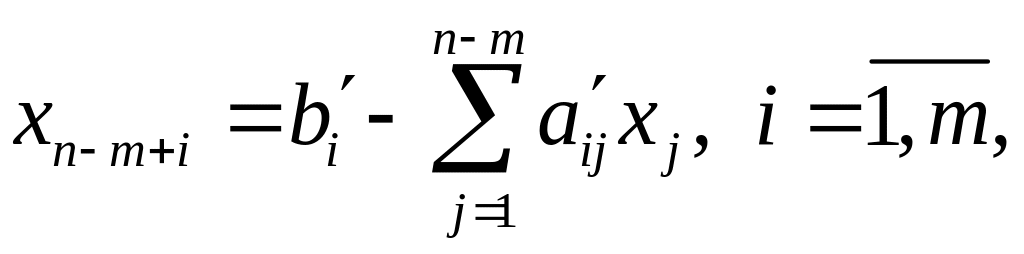
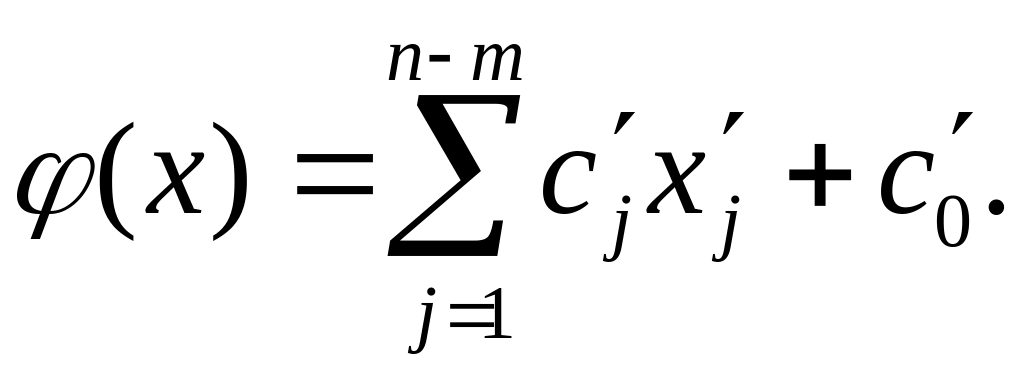
При этом «преобразованные уравнения» записываются следующим образом:

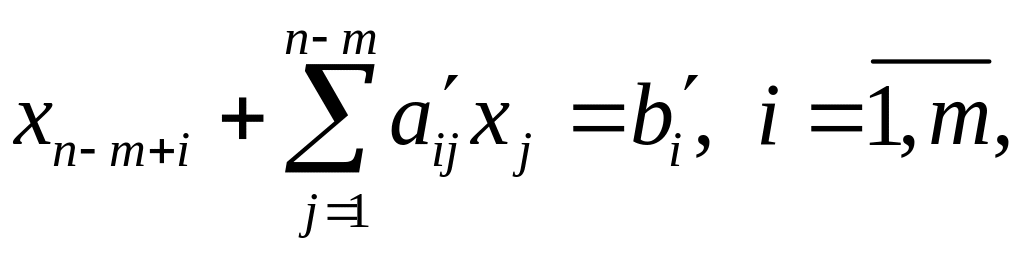
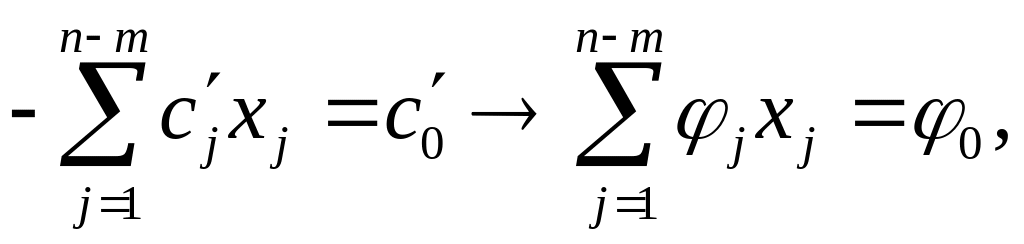
где

Для рассматриваемого случая симплекс-таблица имеет вид

Базис	Св. член	x1	∙∙∙	xn-m	xn-m+1	xn-m+2	∙∙∙	xn
xn-m+1	b′1	a′11	∙∙∙	a′1,n-m	1	0	∙∙∙	0
xn-m+2	b′2	a′21	∙∙∙	a′2,n-m	0	1	∙∙∙	0
∙ ∙ ∙	∙ ∙ ∙	∙ ∙ ∙	∙∙∙ ∙∙∙ ∙∙∙	∙ ∙ ∙	∙ ∙ ∙	∙ ∙ ∙	∙∙∙ ∙∙∙ ∙∙∙	∙ ∙ ∙
xn	b′m	a′m1	…	a′m,n-m	0	0	∙∙∙	1
φ	φ0	φ1	…	φn-m	0	0	∙∙∙	0

Таким образом, в целевой строке все коэффициенты целевой функции, кроме свободного члена, записываются с противоположными знаками.

Для приведенной симплекс-таблицы базис (Б), базисное решение (БР) и значение целевой функции определяются из соотношений

Б = {x_n-m+1, x_n-m+2, …, x_n},

БР = (x₁=0, x₂=0, …, x_n-m=0, x_n-m+1=b′_1, x_n-m+2=b′_{2, …,} x_n=b′_m),

φ (x₁=0, x₂=0, …, x_n-m=0) = φ₀.

Базисное решение, удовлетворяющее условию неотрицательности базисных переменных, называется допустимым базисным решением (ДБР).

Симплекс-метод является итерационным методом. После построения симплекс-таблицы для текущей итерации ДБР проверяют на оптимальность. Для этого просматривают коэффициенты целевой строки, кроме свободного члена φ₀. В результате может иметь место один из следующих трех случаев:

– среди коэффициентов целевой строки нет отрицательных;

– среди коэффициентов целевой строки есть отрицательные и хотя бы в одном из столбцов, соответствующих этим коэффициентам, нет положительных элементов;

– среди коэффициентов целевой строки есть отрицательные и в каждом из столбцов, соответствующих этим коэффициентам, есть хотя бы один положительный элемент.

В первом случае ДБР является оптимальным. Во втором случае целевая функция не ограничена сверху на множестве допустимых решений. В третьем случае можно перейти от текущего ДБР к следующему ДБР, при котором значение целевой функции увеличится. Этот переход осуществляется исключением из текущего базиса одной базисной переменной и включением в него одной свободной переменной.

В качестве новой базисной переменной выбирают ту свободную переменную x_k, которой соответствует наибольший по абсолютной величине отрицательный коэффициент целевой строки. Столбец, соответствующий вводимой переменной, называется ведущим столбцом (в симплекс-таблице помечается стрелкой: k).

Исключаемой переменной будет та переменная текущего базиса, которой соответствует минимальное из отношений элементов столбца свободных членов к положительным элементам ведущего столбца. Строка, соответствующая исключаемой переменной, называется ведущей строкой (в симплекс-таблице помечается стрелкой: ).

Элемент , стоящий на пересечении ведущей строки и ведущего столбца, называется разрешающим.

Симплекс-таблица, соответствующая новому базису, заполняется по следующим правилам:

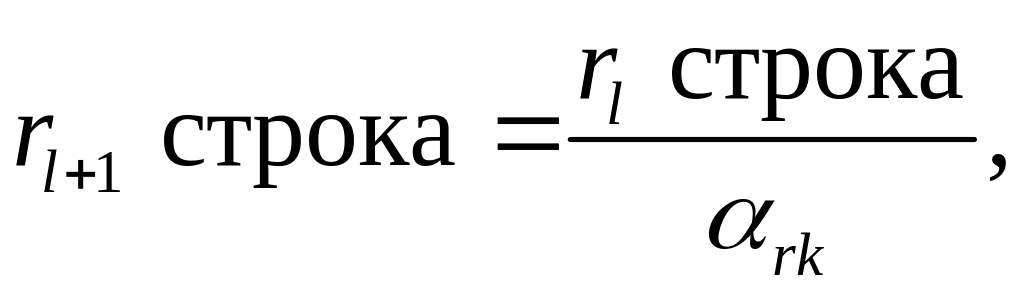(1.15)

(1.16)

(1.17)

где l – номер итерации, l = 0,1,…

Таким образом, алгоритм решения задачи ЛП симплекс-методом заключается в следующем:

1. Приводят задачу ЛП к канонической форме, при этом все свободные члены ограничений должны быть неотрицательными (b_i≥0, ).

2. Определяют начальный базис, составляют симплекс-таблицу и находят начальное ДБР.

3. Проверяют условие оптимальности полученного ДБР: в целевой строке все коэффициенты, кроме свободного члена, являются неотрицательными.

Если условие выполняется, то ДБР определяет решение x^* задачи ЛП, при этом f^* f(x^*)=φ₀.

Если условие не выполняется, то переходят к п. 4.

4. Проверяют условие разрешимости задачи ЛП: в каждом из столбцов, соответствующих отрицательным коэффициентам целевой строки, есть хотя бы один положительный элемент.

Если условие не выполняется, то задача ЛП неразрешима.

Если условие выполняется, то переходят к п. 5.

5. Находят свободную переменную, вводимую в базис, и базисную переменную, исключаемую из базиса. Вводимая переменная определяется наибольшим по абсолютной величие отрицательным коэффициентом, кроме свободного члена, целевой строки; а исключаемая переменная – минимальным из отношений элементов столбца свободных членов к положительным элементам ведущего столбца. В результате получают новый базис.

6. Используя соотношения (1.15) (1.17), составляют симплекс-таблицу, соответствующую новому базису, и находят следующее ДБР. Затем переходят к п. 3.

Вычисления завершают, когда найдено оптимальное решение (п. 3), либо когда задача неразрешима (п. 4).

Определение начальных базиса Б₀ и допустимого базисного решения ДБР₀ не вызывает трудностей, когда задача ЛП задана в сопряженной канонической форме, т.е. в виде (1.8) (1.10), причем все b_i в (1.9) неотрицательны, т.е. b_i≥0, . Тогда для решения задачи ЛП симплекс-методом ее следует привести к канонической форме, вводя дополнительные переменные x_n+i, . Поскольку определитель Δ матрицы коэффициентов при дополнительных переменных отличен от нуля (Δ=1), то совокупность этих переменных может использоваться в качестве начального базиса Б₀, т.е.

Б₀ = { x_n+1, x_n+2, …, x_n+m},

при этом

ДБР₀ = ( x₁=0, x₂=0, …, x_n=0, x_n+1=b_1, x_n+2=b₂, …, x_n+m=b_m).

Если система ограничений в задаче ЛП при неотрицательных свободных членах представлена неравенствами вида «≥» или равенствами, то начальный базис не может быть найден так просто. В таких случаях для его нахождения может использоваться метод искусственных переменных.

Пусть задача ЛП задана в канонической форме, т.е. в виде (1.5) (1.7), причем все свободные члены в (1.6) неотрицательны. Алгоритм нахождения начального базиса методом искусственных переменных заключается в следующем:

1. В ограничения-равенства (1.6) вводят неотрицательные искусственные переменные z_i≥0, , по схеме

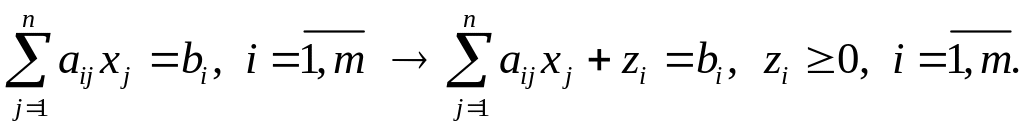
2. Формируют вспомогательную задачу минимизации суммы искусственных переменных при исходных ограничениях, видоизмененных за счет введения искусственных переменных, т.е. задачу вида

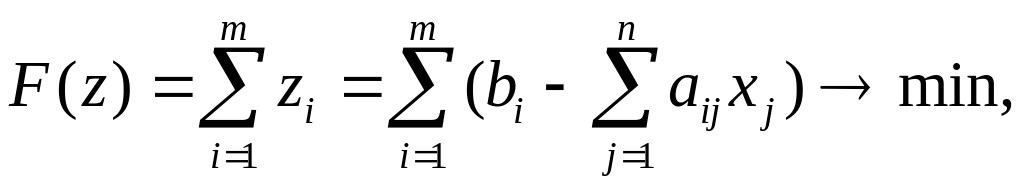
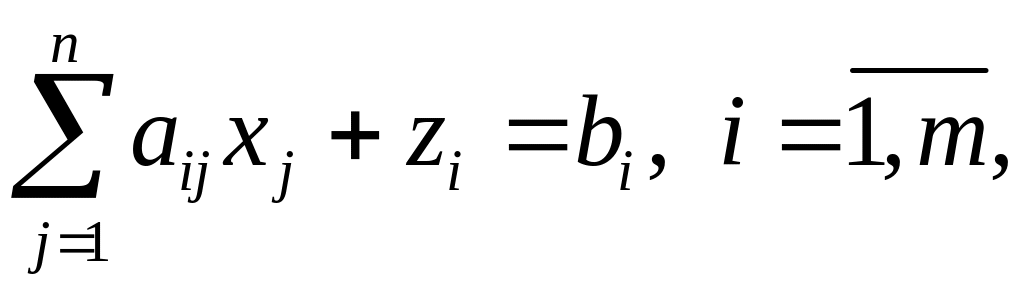
3. Используя симплекс-метод, решают вспомогательную задачу, при этом искусственные переменные образуют начальный базис.

4. Анализируют результаты решения вспомогательной задачи.

Если min F(z)=0, то полученные оптимальные базис и ДБР вспомогательной задачи являются начальными базисом и ДБР исходной задачи.

Если min F(z)>0, то исходная задача не имеет решения.

Следует отметить, что число вводимых в уравнения (1.6) задачи ЛП искусственных переменных может быть и меньше m. Если есть возможность из уравнений (1.6) просто найти s<m базисных переменных из числа «основных» переменных x_j, то можно ввести лишь (m−s) искусственных переменных z_i, При этом начальный базис вспомогательной задачи будет содержать s «основных» переменных x_j и (m−s) искусственных переменных z_i.

Задачи

1.7. Решить симплекс-методом (с помощью симплекс-таблиц) задачу ЛП

f(x)=3x₁+2x₂  max,

x₁−x₂≤2,

2x₁+x₂≤6,

x₁, x₂≥0.

1.8. Пищевой рацион должен содержать не менее восьми единиц вещества А и не менее десяти единиц вещества В.

Имеется 2 вида продуктов питания: П₁ и П₂. В единице продукта П₁ содержатся 1 единица вещества А и 2 единицы вещества В; в единице продукта П₂ содержатся 2 единицы вещества А и 1 единица вещества В. Цена единицы продукта П₁ составляет 3 д.е., цена единицы продукта П₂ – 2 д.е.

Определить, какое требуется количество продуктов П₁ и П₂, чтобы обеспечить заданные условия при минимальной стоимости рациона.

Составить математическую модель задачи. Решить полученную задачу ЛП симплекс-методом.