4.2. Детерминированные динамические модели
На практическом занятии рассматриваются N-этапные динамические модели, для которых предполагается:
− спрос известен, но он может меняться от этапа к этапу;
− пополнение запаса происходит мгновенно в начале этапа;
− дефицит отсутствует;
− после N этапов не остается неиспользованной продукции.
При описании этапа
используются следующие величины:
Qi – количество заказанной продукции (размер заказа),
ξi – потребность в продукции (спрос),
xi – исходный запас (на начало этапа i),
hi – затраты на хранение единицы запаса, переходящей из этапа i в этап i+1,
Ki – затраты на оформление заказа,
Ci(Qi) – затраты на приобретение продукции в размере Qi,
Ui(Qi) – затраты на оформление заказа и приобретение продукции.
Затраты Ui(Qi) определяются следующим образом:
Ui(Qi) =δi Ki + Ci(Qi),
где
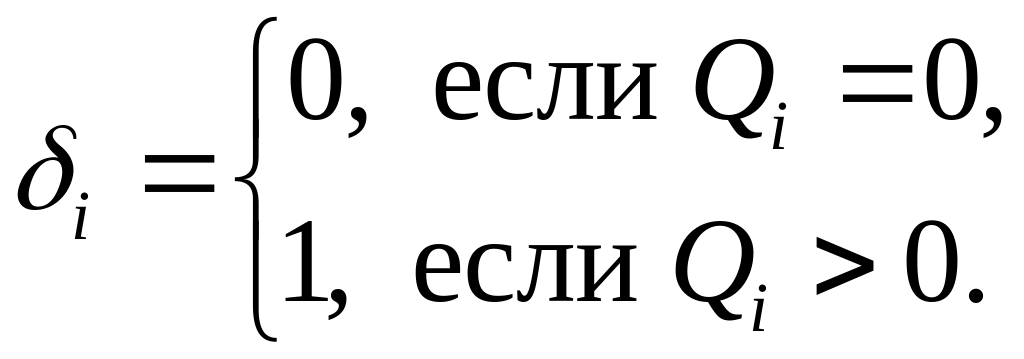
Затраты на хранение на i-м этапе предполагаются (с целью упрощения) пропорциональными объему запаса xi+1 и, следовательно, равными hi xi+1.
В данной задаче управления запасами требуется найти оптимальные значения Qi, минимизирующие общие затраты на оформление заказов, закупку и хранение по всем N этапам.
Рассматриваемую задачу удобно представить схематически (см. рис. 4.3).
Из приведенной схемы следует, что
xi+1
= xi
+
Qi
– ξi,
(4.3)
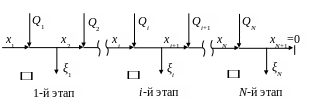
Рис. 4.3
Границы изменения (нижняя и верхняя) размера заказа Qi и объема запаса xi+1 определяются из соотношений
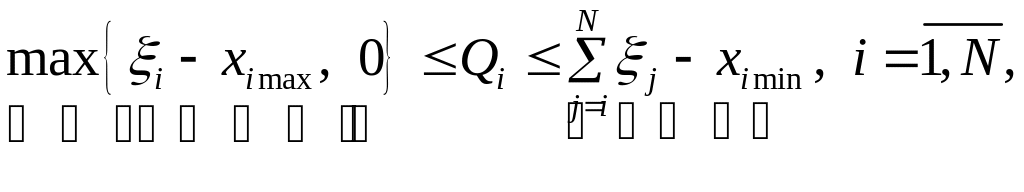(4.4)
Qimin Qimax
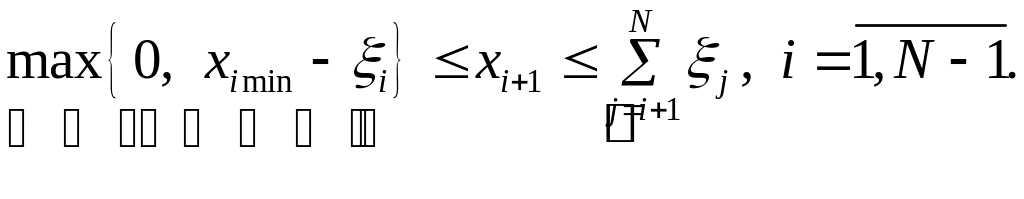(4.5)
xi+1,min xi+1,max
Значения ximin, ximax , используемые в приведенных выражениях, определяются на предыдущем ((i−1)-м) этапе.
Для решения поставленной задачи используется рекуррентное уравнение
(4.6)
(4.7)
где через
обозначены минимальные
общие затраты на этапах от 1 до i
при заданной величине запаса xi+1
на конец этапа i.
Таким образом,
процедура решения состоит из N
этапов. На i-м,
этапе определяются наборы значений
и Qi
для
Результаты вычислений для каждого этапа
заносят в таблицы, общий вид которых
представляет табл. 4.1.
При этом для 1-го этапа заголовок таблицы имеет вид
.
Таблица 4.1
xi+1 |
hi xi+1 |
|
Оптим. решение |
|||
Qi,min |
∙∙∙ |
Qi,max |
|
Q*i |
||
Ui(Qi,min) |
∙∙∙ |
Ui(Qi,max) |
||||
xi+1,min |
hi xi+1,min |
|
|
|
|
|
. . . |
. . . |
|
|
|
|
|
xi+1,max |
hi xi+1,max |
|
|
|
|
|
В строках выделенной
части таблицы записывают значения
величины
при соответствующих данным строкам
значениях xi+1.
В последних двух клетках каждой строки
записывают минимальное при заданном
xi+1
значение затрат
и значение Q*i,
обеспечивающее этот минимум.
При вычислении
для
значения
выбирают из столбца «Оптимальное
решение» таблицы для предыдущего
((i−1)-го)
этапа. При этом, используя выражение
(4.3), определяют величину xi
из соотношения
При заполнении
таблицы для 1-го этапа (этапа определения
из соотношения (4.6)) в каждой строке
выделенной части таблицы будет одно
число. Это объясняется следующим
обстоятельством. Величина x2
определяется
из соотношения
Поскольку x1 задано, ξ1 задано, то выбранное Q1 однозначно определяет x2.
Таким образом, алгоритм i-го, i=1,2,…,N, этапа заключается в следующем:
1. Используя соотношения (4.4) и (4.5), определяют границы изменения размера заказа Qi и объема запаса xi+1 (на 1-м этапе полагают x1min=x1max=x1, на N-м этапе – xN+1=0).
2. Строят таблицу для записи числовых результатов.
3. В выделенную часть таблицы построчно заносят результаты вычислений
Заполнив очередную строку, определяют для данного xi+1 величины и Qi*.
Полученные после
N-го
этапа затраты
представляют собой минимальные общие
затраты по всем N
этапам, т.е.
.
Вектор
находится в результате обратного прохода
по таблицам этапов.
Из таблицы для
N-го
этапа определяется
.
Для нахождения
используются затраты
,
входящие в качестве слагаемого в затраты
;
величина
,
соответствующая затратам
,
определяется из таблицы (N−1)-го
этапа. Для нахождения
используются затраты
,
входящие в качестве слагаемого в затраты
найденные на предыдущем шаге; величина
определяется из таблицы (N−2)-го
этапа и т.д. Таким образом, компоненты
вектора Q*
находят по следующей схеме:
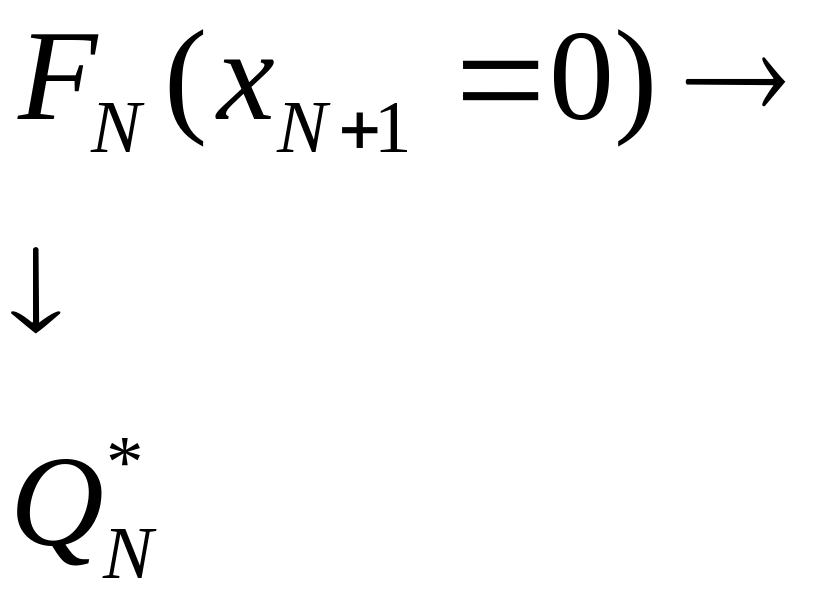
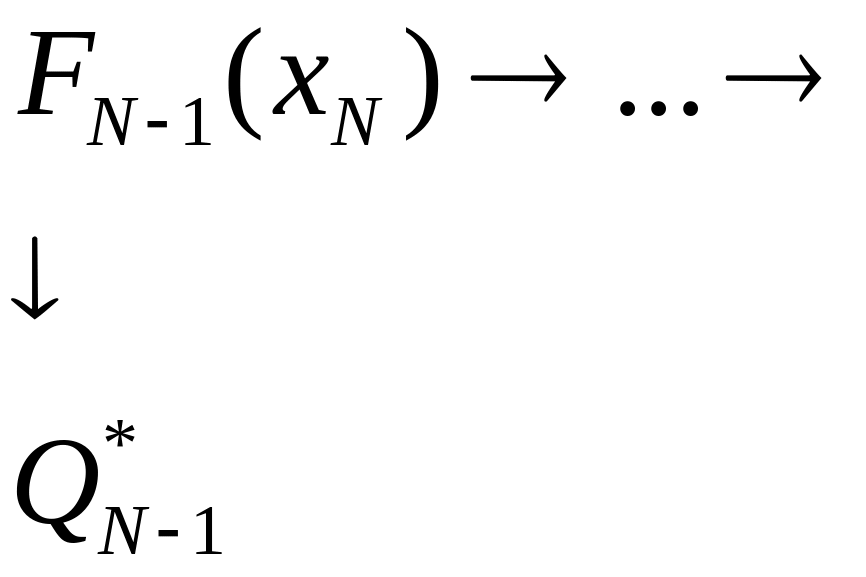
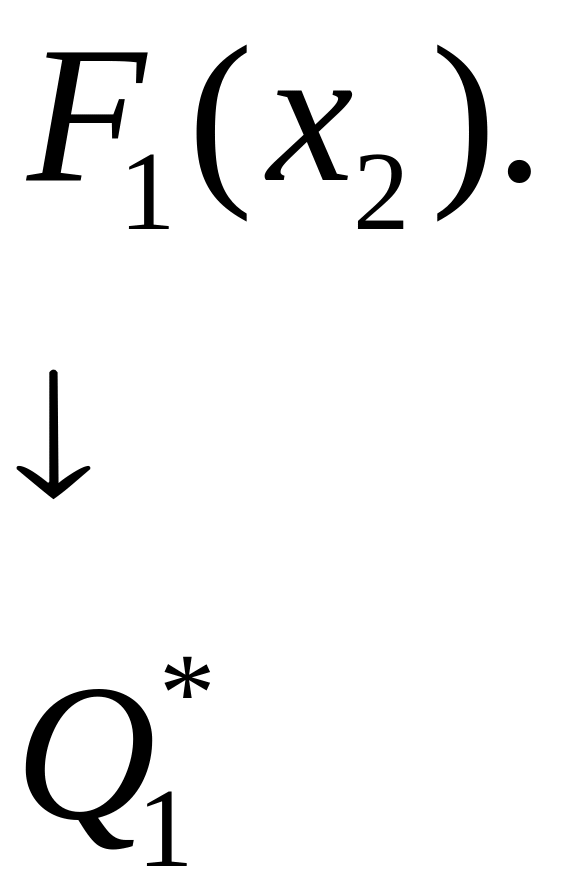
Рассмотренную детерминированную динамическую модель можно использовать при любых функциях затрат. Важным частным случаем этой модели является такой, когда на i-м этапе как затраты на приобретение, так и затраты на хранение на единицу продукции являются постоянными или убывающими функциями Qi и xi+1 соответственно.
При указанных условиях доказаны следующие положения (при исходном уровне запаса x1=0; если x1>0, то этот объем нужно вычесть из спроса первого и последнего этапов, пока он не исчерпается).
1. На любом этапе
i
произведение оптимальных значений
исходного запаса
и размера заказа
должно быть равно 0, т.е.
(4.8)
2. На любом этапе i оптимальный размер заказа равен 0 или спросу одного или более последующих этапов, т.е.
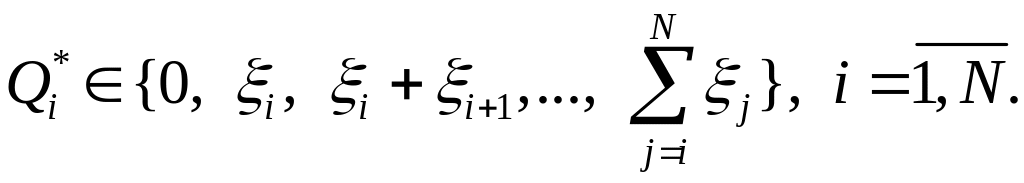(4.9)
При этом оптимальное
значение объема запаса
определяется из следующего множества
возможных значений:
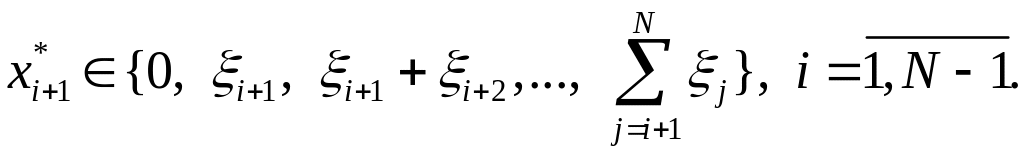
Поскольку x1=0,
то из соотношения (4.9) следует, что
Благодаря приведенным положениям упрощается вычислительная схема. Число возможных значений как Qi, так и xi+1 определяется числом последующих этапов, а не количеством единиц продукции, требуемой на последующих этапах, как это имеет место в обычной модели. Кроме того, при заполнении таблиц не следует рассматривать наборы (Qi, xi), не удовлетворяющие условию (4.8), поскольку они заведомо не являются оптимальными. В результате объем вычислений весьма существенно сокращается.
Задачи
4.5. Для четырехэтапной динамической модели исходный запас для этапа 1 равен 4 ед. Спрос на этапах соответственно составляет 2 ед., 3 ед., 5 ед. и 4 ед. Определить множество возможных значений исходного запаса для этапов 2, 3 и 4 и множество возможных значений размера заказа на этапах 1, 2, 3 и 4.
4.6. Для трехэтапной динамической модели исходный запас для этапа 1 равен 1 ед. Спрос на этапах соответственно составляет 3 ед., 2 ед. и 4 ед. Затраты на размещение заказа на этапах соответственно равны 3 д.е., 7 д.е. и 6 д.е. Затраты на хранение единицы продукции в течение одного этапа соответственно составляют 1 д.е., 3 д.е. и 2 д.е. Цена единицы продукции равна 10 д.е. на всех этапах.
Определить оптимальные размеры заказов и минимальные суммарные затраты.
4.7. Для четырехэтапной динамической модели исходный запас для этапа 1 равен 15 ед. Спрос на этапах соответственно составляет 76 ед., 26 ед., 90 ед. и 67 ед. Затраты на размещение заказа на этапах соответственно равны 98 д.е., 114 д.е., 185 д.е. и 70 д.е. Затраты на хранение единицы продукции в течение одного этапа составляют 1 д.е. на всех этапах. Цена единицы продукции равна 2 д.е. на всех этапах.
Определить оптимальные размеры заказов и минимальные суммарные затраты.
Ответы
1.1.
–f(x)=x1−2x2+x3−x4→max,
2x1−x2−x3+x4+x5=6,
−x1−2x2−x3+x4+x6=−8,
−x1+3x2+5x3−3x4=15,
1.2. Для базисной переменной x3
φ(x)=−12x1+6x2+20→max,
−4x1+4x2≤−6,
−3x1≤−9,
2x1−x2≤4,
x1, x2≥0.
1.3. Для базисных переменных x3, x4, x5
−φ(x)=4x1+3x2−3→max,
x1+2x2≤3,
−3x1−3x2≤−4,
3x1−x2≤2,
x1, x2≥0.
1.4. x*=(2,4), f*=16.
1.5. x*=(0,6), f*=−18.
1.6. x*=(5/6,1/2), f*=−1/2.
1.7. x*=(0,6), f*=12.
1.8. Рацион, состоящий из 4 единиц продукта П1 и 2 единиц продукта П2, обеспечивает заданные условия по содержанию веществ А и В и имеет минимальную стоимость 16 д.е.
1.9.
F(y)=y1−4y2−3y3→min,
2y1−y2−y3≥1,
−y1+y2+y4=−10,
−2y2+y3+y4≥2,
y2−y4=−1,
−y2−2y3=7,
y1≥0, y2≥0, y3≥0.
1.10. Рацион, состоящий из 2 единиц продукта П1 и 6 единиц продукта П2, обеспечивает заданные условия по содержанию веществ A, B, C и D и имеет минимальную стоимость 18 д.е.
1.11.
X0,СЗУ= |
120 |
|
|
|
X0,МЭ= |
|
120 |
|
|
40 |
10 |
|
|
|
|
50 |
|
||
|
130 |
60 |
, |
160 |
|
30 |
. |
||
|
|
110 |
|
|
20 |
90 |
|
1.12.
X0,СЗУ= |
4 |
2 |
|
|
|
X0,МЭ= |
|
6 |
|
|
|
|
4 |
4 |
|
, |
|
|
2 |
6 |
. |
||
|
|
4 |
6 |
|
4 |
0 |
6 |
|
|
Минимальные транспортные издержки, равные 40 д.е., имеют место при следующем плане перевозок: с 1-го предприятия перевозят 6 ед. продукции во 2-й магазин, со 2-го предприятия − 2 ед. продукции в 3-й магазин и 6 ед. продукции в 4-й магазин, с 3-го предприятия − 4 ед. продукции в 1-й магазин и 6 ед. продукции в 3-й магазин.
2.1. О1 − выигрыш 500 д.е., u1=25; О2 − выигрыш 200 д.е., u2=10; О3 − выигрыш 100 д.е., u3=5; О4 − выигрыш 50 д.е., u4=2,5; О5 − выигрыш 20 д.е., u5=1.
2.2. О1 − добраться к месту работы на такси, u1=12; О2 − добраться к месту работы на трамвае, u2=3; О3 − добраться к месту работы пешком, u3=1.
2.3. u1=8,5; u2=5; u3=3; u4=1,5; u5=1.
2.4.
О1: Q1 и Q2, p(O1)=0;
O2:
Q1
и
,
p(O2)=1/6;
O3:
и Q2,
p(O3)=1/6;
O4:
p(O4)=4/6.
2.5. Наибольшая эффективность стрельбы достигается при среднем количестве израсходованных боеприпасов.
2.6. Фабрике следует изготовить:
− в случае критерия Лапласа − 20 пальто,
− в случае критерия Гурвица – 80 пальто.
2.7. Продавец должен заказать:
− в случае критерия Вальда – 10 газет,
− в случае критерия Лапласа – 30 газет,
− в случае критерия Гурвица – 50 газет,
− в случае критерия Сэвиджа – 40 газет.
2.8. Продавец должен заказать 30 газет.
2.9. Оптимальной является стратегия c5.
2.10.
|
u1 |
u2 |
u3 |
u4 |
c5 |
5 |
2 |
4 |
3 |
c1 |
5 |
2 |
2 |
5 |
c6 |
4 |
3 |
2 |
5 |
c7 |
4 |
2 |
4 |
5 |
c3 |
4 |
2 |
4 |
3 |
c2 |
3 |
3 |
2 |
5 |
c4 |
3 |
2 |
4 |
3 |
2.11. Оптимальной является стратегия c3.
3.2. Как японцам, так и американцам следует выбрать северный путь, при этом конвой будет подвергаться бомбардировке 2 дня.
3.3. α*= α1, β*= β2, u=v=1.
3.4. Первому игроку в 60% игр следует выбирать число 1 и в 40% игр – число 2; второму игроку в 20% игр следует выбирать число 1 и в 80% игр − число 2. Средний проигрыш первого игрока составит 0,4 рубля.
3.5. Первому игроку в 2/3 от общего числа игр следует выкладывать 1 рубль и в 1/3 от общего числа игр − 2 рубля; второму игроку в 1/2 от общего числа игр следует выкладывать 1 рубль и в 1/2 от общего числа игр − 2 рубля. Средний результат игры – ничья.
3.6. Первому игроку в 2/7 от общего числа игр следует выбирать герб, а в 5/7 от общего числа игр – цифру; второму игроку в 4/7 от общего числа игр следует выбирать герб, а в 3/7 от общего числа игр − цифру. Средний выигрыш второго игрока составит 1/7 рубля.
3.7. Второму игроку следует выбирать число 4, если первый игрок выбрал число 1, и число 3, если первый игрок выбрал число 2. Средний выигрыш второго игрока составит 4,2 рубля.
3.8. Первому игроку в 54% игр следует выбирать число 1 и в 46% игр − число2; второму игроку также в 54% игр следует выбирать число 3 и в 46% игр − число 4. Средний результат игры близок к 0 (практически ничья).
3.9. X0=(3/5,2/5), Y0=(2/5,3/5), u=v=1/5. Защитная пара стратегий (X0, Y0) не является уравновешенной.
3.10. Пара стратегий (X′,Y′) является уравновешенной.
3.11. Пара стратегии (X″, Y″) является уравновешенной.
4.1. Оптимальный размер заказа составляет 1000 единиц продукции, оптимальный интервал времени между моментами размещения заказов − 10 дней, минимальные суммарные затраты − 60 д.е. в день.
4.2. Дневные затраты при применяемой стратегии превышают дневные затраты при оптимальной стратегии на 81 д.е.
4.3. Оптимальный размер заказа составляет 15 изделий.
4.4. Оптимальный размер заказа составляет: для 1-го вида продукции − 6,7 единиц; для 2-го вида продукции − 7,6 единиц; для 3-го вида продукции − 10,6 единиц.
4.5.
4.6. Оптимальные размеры заказов на этапах соответственно составляют 4 ед., 0 ед. и 4 ед. продукции; минимальные суммарные затраты равны 91 д.е.
4.7. Оптимальные размеры заказов на этапах соответственно составляют 61 ед., 116 ед., 0 ед. и 67 ед. продукции; минимальные суммарные затраты равны 860 д.е.