
- •По курсу
- •Для студентов специальности 080801
- •Таганрог 2007
- •1. Линейное программирование (лп)
- •1.1. Формы представления задач лп
- •1.2. Графический метод решения задачи лп
- •1.3. Симплекс-метод решения задачи лп
- •1.4. Двойственные задачи лп
- •1.5. Транспортная задача
- •2. Некоторые принципы принятия решений в задачах исследования операций
- •2.1. Задачи принятия решений. Определение
- •Полезности
- •2.2. Однокритериальные задачи принятия решений
- •2.3. Многокритериальные задачи принятия решений
- •3. Игровые методы принятия решений
- •3.1. Игры в матричной форме. Решение матричных антагонистических игр в чистых стратегиях
- •3.2. Решение матричных антагонистических игр в смешанных стратегиях
- •3.3. Игры в позиционной форме
- •3.4. Неантагонистические игры (некооперативный вариант)
- •4. Модели управления запасами
- •4.1. Детерминированные статические модели
- •4.2. Детерминированные динамические модели
- •Библиографический список
- •Содержание
- •1.1. Формы представления задач лп……………..………….……..3
- •Математические методы и модели исследования операций
 № 4072
№ 4072

Министерство образования и науки
российской федерации
федеральное агентство по образованию
Технологический институт
Федерального государственного образовательного учреждения
высшего профессионального образования
«Южный федеральный университет»
М ЕТОДИЧЕСКИЕ
УКАЗАНИЯ
ЕТОДИЧЕСКИЕ
УКАЗАНИЯ
К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ
По курсу
МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ
ИССЛЕДОВАНИЯ ОПЕРАЦИЙ
Для студентов специальности 080801
Таганрог 2007
удк 518.5.001.57(07.07)+519.8(07.07)
Составитель Б.Ф. Харчистов
Методические указания к практическим занятиям по курсу «Математические методы и модели исследования операций». – Таганрог: Изд-во Технологического института ЮФУ, 2007. – 64 с.

Изложены основные понятия и теоретические положения курса «Математические методы и модели исследования операций», используемые при решении задач. Приведены алгоритмы реализации различных математических методов. Каждый подраздел содержит задачи, снабженные ответами. Предназначены для студентов специальности 080801 «Прикладная информатика в экономике», а также преподавателей, проводящих практические занятия по данному предмету.
Илл. 3. Библиогр.: 6 назв.
Рецензент О.Д. Глод, канд. техн. наук, доцент каф. СА и Т Технологического института ЮФУ.
1. Линейное программирование (лп)

1.1. Формы представления задач лп
В общем случае задача ЛП записывается следующим образом:
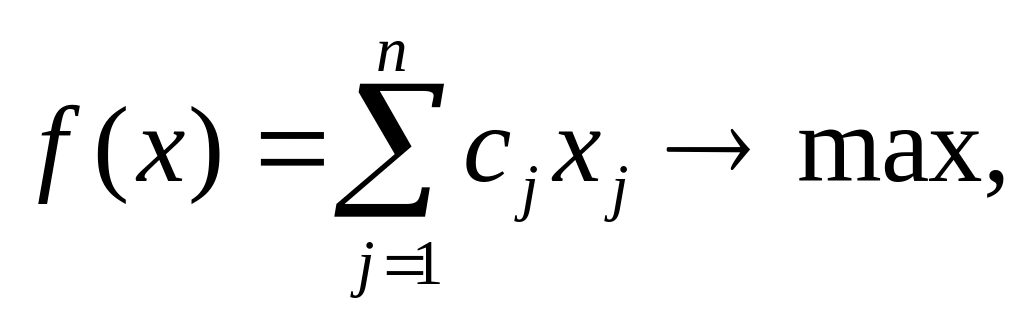 (1.1)
(1.1)
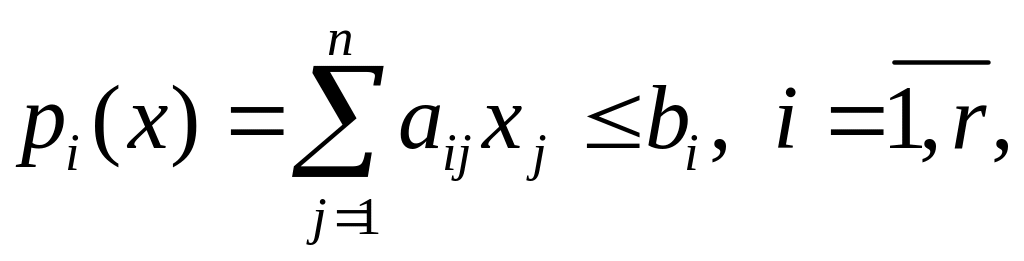 (1.2)
(1.2)
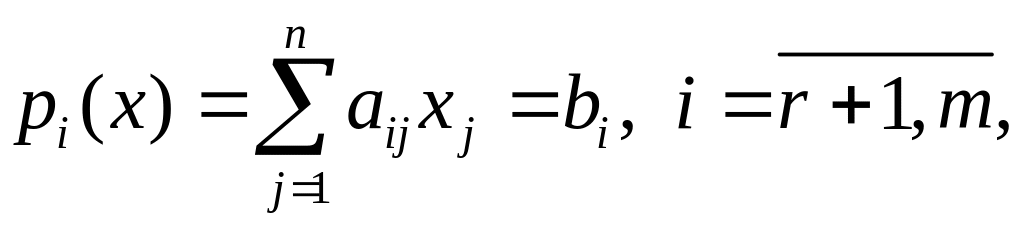 (1.3)
(1.3)
![]() (1.4)
(1.4)
где сj,
aij,
bi
– заданные постоянные величины и r![]() m.
m.
Считается, что все уравнения системы (1.3) являются линейно независимыми, при этом m–r≤n. На практике рассматривается только случай m–r<n (случай m–r=n – тривиальный, поскольку дает единственное решение для совместной системы уравнений (1.3)).
В случае, когда исходная задача ЛП является задачей минимизации f(x), от нее можно перейти к задаче максимизации (–f(x)), поскольку min f(x) = −max (–f(x)).
В случае, когда исходная задача ЛП содержит ограничения-неравенства вида «≥», от них можно перейти к ограничениям-неравенствам вида «≤», меняя в исходных ограничениях знаки свободных членов и коэффициентов на противоположные. Например, от ограничения
![]()
можно перейти к ограничению
![]() .
.
Общая задача ЛП, в которой все ограничения (кроме условий (1.4) неотрицательности переменных) заданы в виде равенств, т.е.
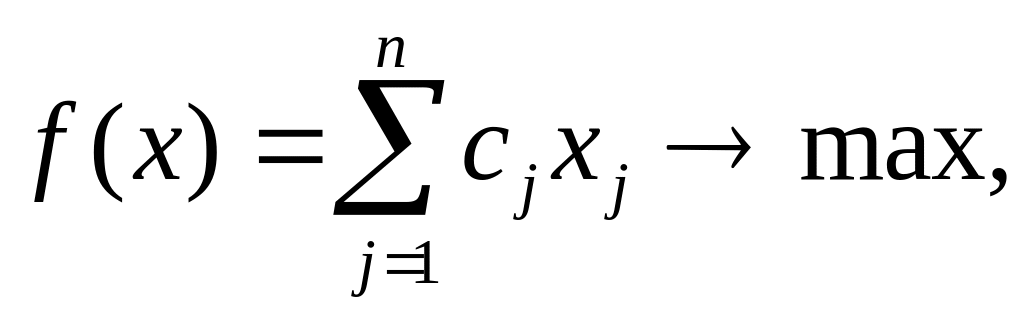 (1.5)
(1.5)
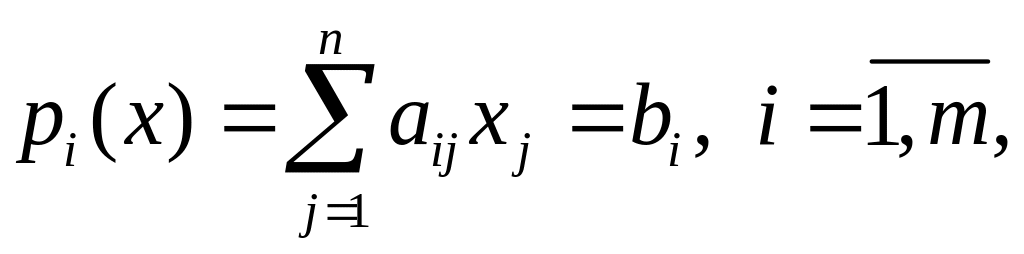 (1.6)
(1.6)
![]() (1.7)
(1.7)
называется задачей ЛП в канонической форме. В данном случае r=0, s=n и m<n.
Алгоритм приведения общей задачи ЛП к задаче в канонической форме заключается в следующем.
Ограничения-неравенства
(1.2) преобразуются в равенства посредством
введения дополнительных
неотрицательных переменных xn+i,
![]() по схеме
по схеме
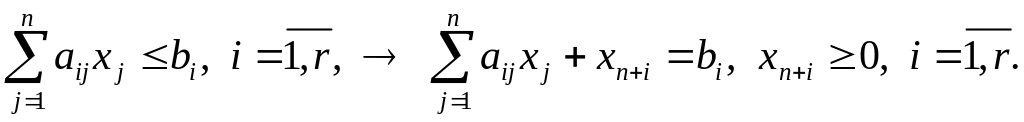
Таким образом, при переходе от общей задачи ЛП к задаче в канонической форме получаем m ограничений-равенств с n+r переменными.
Общая задача ЛП, в которой все ограничения заданы в виде нестрогих неравенств, т.е.
(1.8)
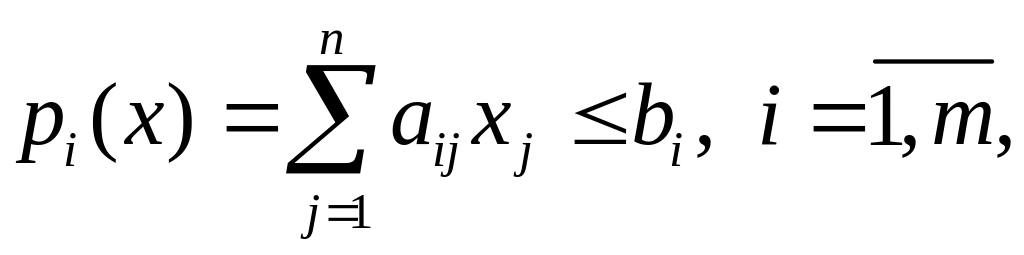 (1.9)
(1.9)
(1.10)
называется задачей ЛП в сопряженной канонической форме. В данном случае r=m и s=n.
Алгоритм приведения общей задачи ЛП к задаче в сопряженной канонической форме заключается в следующем:
1. Из переменных
xj
системы
уравнений (1.3) выбирают m−r
переменных, для которых определитель
матрицы коэффициентов отличен от нуля
(базисные
переменные). Пусть для определенности
базисными переменными являются
переменные xn-m+r+1![]() xn,
тогда переменные x1
xn-m+r
являются
свободными
переменными.
xn,
тогда переменные x1
xn-m+r
являются
свободными
переменными.
2. Из уравнений системы (1.3) базисные переменные выражаются через свободные. Для выбранных в п.1 базисных и свободных переменных получим
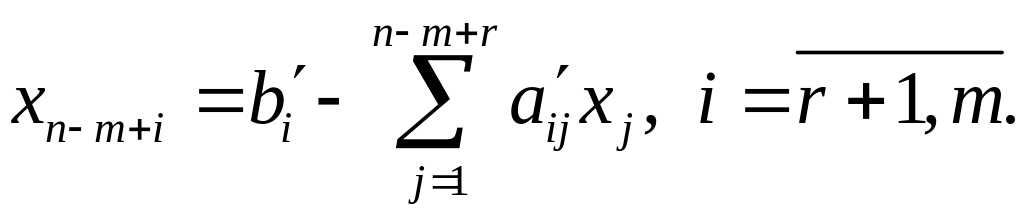 (1.11)
(1.11)
3. Из условий неотрицательности базисных переменных
![]()
находят ограничения задачи ЛП в виде нестрогих неравенств
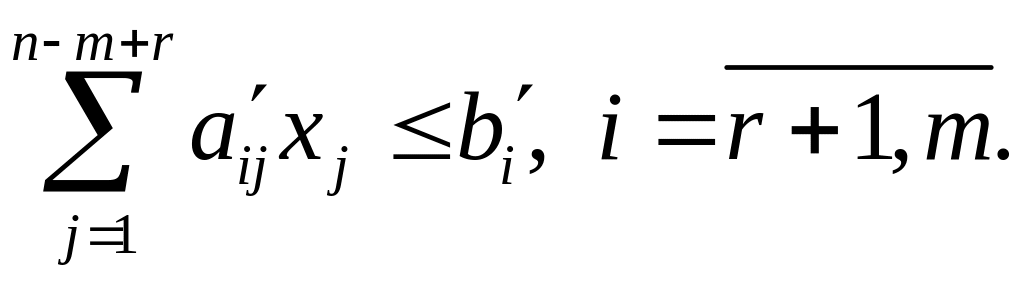
4. Базисные переменные из соотношений вида (1.11) подставляют в условия (1.2), в результате получают ограничения в виде нестрогих неравенств, зависящие только от свободных переменных,
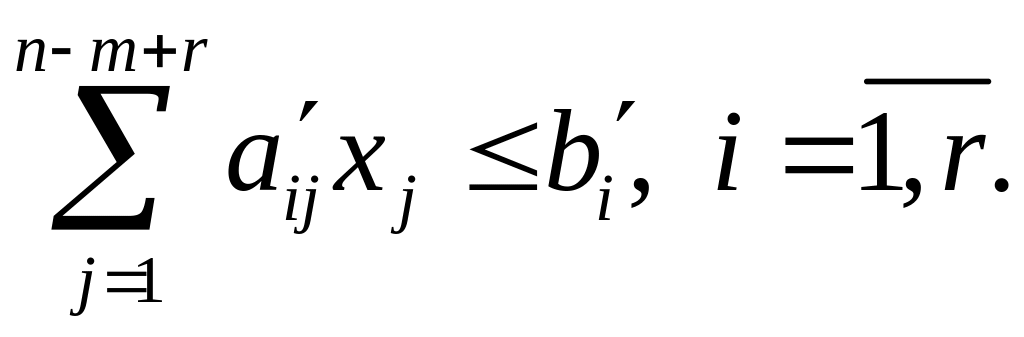
5. Базисные переменные из соотношений вида (1.11) подставляют в выражение для целевой функции (1.1), в результате получают целевую функцию, зависящую только от свободных переменных. Для выбранных в п.1 базисных и свободных переменных получим
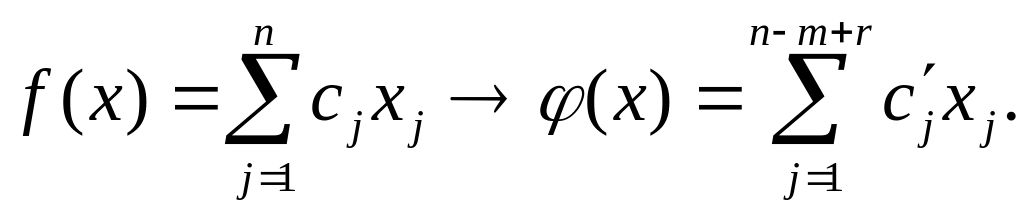
Таким образом, при переходе от общей задачи ЛП к задаче в канонической форме получаем m ограничений-неравенств с n−m+r неизвестными.
По рассмотренным алгоритмам можно также переходить от задачи в канонической форме к задаче в сопряженной канонической форме и наоборот.
Задачи
1.1.Записать задачу ЛП
f(x) = −x1+2x2−x3+x4 min,
2x1−x2−x3+x4≤6,
x1+2x2+x3−x4≥8,
−x1+3x2+5x3−3x4=15,
![]()
в канонической форме.
1.2. Записать задачу ЛП
f(x) =−2x1+x2+5x3 max,
2x1+x2+3x3≤6,
x1+x2−x3≥5,
2x1−x2+x3=4,
![]()
в сопряженной канонической форме.
1.3. Записать задачу ЛП
f(x) = x1−3x2−x3−x4+x5 min,
2x1+x2−x3−x4=1,
−x1+x2+2x3+x4=2,
x1−2x2+x3+x4+x5=1,
![]()
в сопряженной канонической форме.
