Министерство образования Российской Федерации

КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н. ТУПОЛЕВА

_______________________________________________________________

Н.Е.РОДНИЩЕВ, С.Н.МЕДВЕДЕВА

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Методические указания по проведению практических занятий

Казань 2012

Практические занятия по учебной дисциплине «Теория вероятностей и математическая статистика» проводятся по темам:

• Случайные события

• Случайные величины

• Системы случайных величин

Используются следующие учебные пособия:

1. Учебное пособие [4] Курс теории вероятностей и математической статистики. Казань, КГТУ, 2007. (электр.издание).

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей, математической статистике. М., Высшая школа, 2005.

Рекомендуется следующая схема изучения каждой части:

1. конспектирование теоретического материала по теме в соответствии с настоящими указаниями;

2. проверка усвоения теоретического материала путем ответов на вопросы самопроверки;

3. решение задач для лучшего уяснения теоретических сведений и приобретения практических навыков в применении теории вероятностей.

Часть 1. Случайные события Занятие 1. Действия с событиями. Классическое и геометрическое определение вероятности. Условная вероятность.

Событие – это всякий факт, который может произойти или не произойти в результате эксперимента.

События разделяются на следующие три вида: достоверные,

невозможные и случайные.

Достоверным событием называют событие, которое обязательно произойдет при каждой реализации условий Q. Достоверные события будем обозначать в дальнейшем знаком .

Пример достоверного события – выпадение не более 6 очков при бросании одной игральной кости.

Невозможным событием называют событие, которое заведомо не произойдет при каждой реализации условий Q. Невозможные события будем обозначать знаком .

Пример невозможного события – выпадение 12 очков при бросании одной игральной кости.

Случайным событием называют событие, которое при реализации условий Q может либо произойти, либо не произойти.

Обозначения случайных событий – латинские заглавные буквы начала алфавита, например, событие А, событие В и т.д.

Действия с событиями (алгебра событий) описываются в конспекте лекций (лекция 1) .

Приведем свойства событий:

А+ = ;

А* =А;

А*А=А;

А+А=А;

С(А+В)=сА+сВ;

А+ =А;

А* = ;

(А\В)(В\А)= ;

А+В=В+А;

АВ=ВА;

Классическое определение вероятности.

Если событие А подразделяется на т частных случаев, входящих в полную группу из n попарно несовместимых и равновозможных событий, то вероятность Р(A) события А равна

Решение типовых задач

Пример 1.1.

Формулировка задачи.

Монета брошена 2 раза. Определить вероятность того, что хотя бы 1 раз появится «герб».

Решение.

Шаг 1. Определение события, вероятность которого требуется вычислить.

Если какая-то проблема взята из реальной жизни, то самое трудное и самое важное – сформулировать эту задачу на математическом языке. Основным этапом, от которого напрямую будет зависеть дальнейшее решение задачи, является определение события, вероятность которого требуется вычислить. Неправильно определить событие значит неправильно решить задачу.

Укажем событие, вероятность которого требуется посчитать. Для этого уточним, что тот факт, что хотя бы 1 раз при двух подбрасываниях монеты появится «герб» означает, что «герб» появится 1 раз или 2 раза.

Таким образом, событие А состоит в том, что при подбрасывании монетки «герб» появится 1 раз или 2 раза.

Определим подход, который целесообразнее применить для подсчета вероятности названного события. Задачу можно решать непосредственным подсчетом вероятности данного события А или методом определения вероятности события, противоположного А.

Конечно, разумнее вычислять вероятность противоположного А события, которое состоит в том, что «герб» не появится ни разу, поскольку оно является элементарным. Событие А же представляет собой сумму двух элементарных событий, а именно: события В, состоящего в том, что «герб» появится 1 раз, и события С, состоящего в том, что «герб» появится 2 раза при подбрасывании монетки.

Если мы вычислим вероятность противоположного события, то вероятность события А определим из соображения, что сумма вероятностей события А и противоположного с А события равна 1.

Шаг 2. Определение числа возможных исходов испытания.

При одном подбрасывании монетки число исходов равно 2, тогда при двух подбрасываниях число всех возможных исходов составляет 4.

Значит, n=4.

Шаг 3. Определение числа исходов, благоприятствующих событию, противоположному А.

Событие, противоположное А, состоит в том, что «герб» не появится ни разу, то есть при обоих подбрасываниях монетки выпадет «решка».

Количество исходов, благоприятствующих этому событию, очевидно, равно 1.

Итак, m=1.

Шаг 4. Применение формулы непосредственного подсчета вероятности.

Воспользовавшись формулой непосредственного подсчета вероятности, получим, что вероятность события, противоположного событию А, равна:

m/n = ¼.

Значит, искомая вероятность события А равна:

Р(А) = 1 – ¼ = ¾.

Пример 1.2.

Формулировка задачи.

Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера. Получен­ные кубики тщательно перемешаны. Определить вероятность того, что кубик, извлеченный наудачу, будет иметь две окрашенные стороны.

Решение.

Введем событие А, состоящее в том, что кубик, извлеченный наудачу, будет иметь две окрашенные стороны. Всего кубиков n =1000. Куб имеет 12 ре­бер, на каждом из которых по 8 кубиков с двумя окрашен­ными сторонами. Поэтому m = 12*8 =96, P(A)= = =0,096.

Пример 1.3.

Формулировка задачи.

В партии из n изделий k бракованных. Определить вероятность того, что среди выбранных наудачу для проверки m изделий ровно l окажутся бракованными.

Решение.

Введем событие А, состоящее в том, что среди выбранных наудачу для проверки m изделий ровно l окажутся бракованными. Число возможных способов взять m изделий из n равно . Благоприятствующими являются случаи, когда из общего числа k бракованных изделий взято l (это можно сделать способами), а остальные m – l - изделий не бракованные, т. е. они взяты из общего числа n - k (количество способов равно ). Поэтому число благо­приятствующих случаев равно . Искомая вероятность будет P(A)=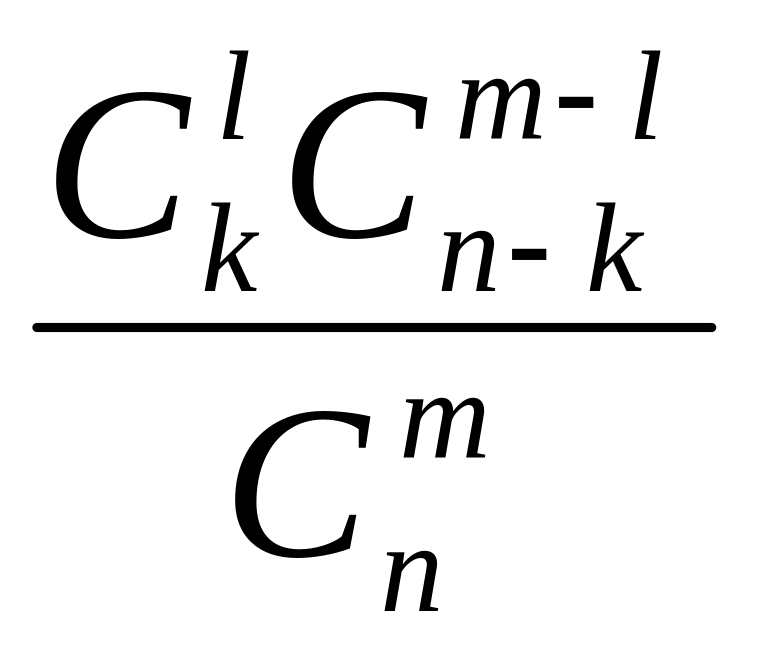

Пример 1.4.

Формулировка задачи.

Из полного набора костей домино наудачу берутся пять костей. Найти вероятность p того, что среди них будет хотя бы одна с шестеркой.

Решение.

Введем событие А, состоящее в том, что среди них будет хотя бы одна с шестеркой. Найдем вероятность q- противоположного события. Тогда p=1 - q. Вероятность того, что все взятые пять костей не содержат шестерки (см. пример 2.2), равна . Поэтому P(A)= .

Задачи для самостоятельной работы

1.1.

Лотерея выпущена на общую сумму n рублей. Цена одного билета r рублей. Ценные выигрыши падают на m билетов. Определить вероятность ценного выигрыша на один билет.

(Ответ: p = )

1.2.

Случайно выбранная кость домино оказалась не дублем. Найти вероятность того, что вторую также взятую наудачу кость домино можно приставить к первой.

(Ответ: p = )

1.3.

В колоде 36 карт четырех мастей. После извлечения и возвращения одной карты колода перемешивается и снова извлекается одна карта. Определить вероятность того, что обе извлеченные карты одной масти.

(Ответ: p = 0.25)

1.4.

Буквенный замок содержит на общей оси пять дисков, каждый из которых разделен на шесть секторов с различными нанесенными на них буквами. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Определить вероятность открытия замка, если установлена произвольная комбинация букв.

(Ответ: p = = 0.00013)

1.5.

В кошельке лежат три монеты достоинством по 20 коп. и семь монет по 3 коп. Наудачу берется одна монета, а затем извлекается вторая монета, оказавшаяся монетой в 20 коп. Определить вероятность того, что и первая извлеченная монета имеет достоинство в 20 коп.

(Ответ: p = )

1.6.

Из партии деталей, среди которых n доброкачест­венных и m бракованных, для контроля наудачу взято s штук. При контроле оказалось, что первые k из s деталей доброкачественны. Определить вероятность того, что следующая деталь будет доброкачественной.

(Ответ: p = )

1.7.

Десять книг на одной полке расставляются наудачу. Определить вероятность того, что при этом три определенные книги окажутся поставленными рядом.

(Ответ: p = )

1.8.

Из десяти билетов выигрышными являются два. Определить вероятность того, что среди взятых наудачу пяти билетов:

а) один выигрышный;

б) оба выигрышных;

в) хотя бы один выигрышный.

(Ответ: а) p = ; б) p = ; в) p = )

1.9.

Для уменьшения общего количества игр 2n команд-спортсменов по жребию разбиваются на две подгруппы. Определить вероятность того, что две наиболее сильные команды окажутся:

а) в разных подгруппах;

б) в одной подгруппе.

(Ответ: а) p = ; б) p = )

1.10.

Из колоды карт (52 карты) наудачу извлекаются три карты. Найти вероятность того, что это будут тройка, семерка и туз.

(Ответ: p = 0.0029)

1.11.

Из колоды в 36 карт наудачу извлекаются три карты. Определить вероятность того, что сумма очков этих карт равна 21, если валет составляет два очка, дама—три, король—четыре, туз—одиннадцать, а остальные карты— соответственно шесть, семь, восемь, девять и десять очков.

(Ответ: p = 0.079)

1.12.

Имеются пять билетов стоимостью по одному рублю, три билета по три рубля и два билета по пять рублей. Наугад берутся три билета. Определить вероятность того, что:

а) хотя бы два из этих билетов имеют одинаковую стоимость;

б) все три билета стоят семь рублей.

(Ответ: а) p = 0,75; б) p = )