Раздел 3 Параметрический синтез типового закона управления объектом на основе методологии расширенного d-разбиения
3.1 Исходные данные
В качестве объекта управления системы автоматического управления возьмем канал – .
Исходная передаточная функция ОУ, представленная в канонической последовательно-структурированной форме, имеет вид:
Параметры передаточной функции ОУ:
коэффициент передачи
;порядок астатизма
;полином числителя:
;полином знаменателя:
.
Требования, предъявляемые к синтезируемой системе: устойчивая система с минимальным временем регулирования и перерегулированием.
3.2 Построение параметрических областей заданного качества в среде MathCAD с использованием САПР-файла “MPS-PID”
Все расчёты проводятся с помощью программного модуля Synt PID-ZU-stat.mcd, который представляет собой MathCAD-файл, построенный в форме жёсткого диалога (результаты расчетов представлены в файле 3.xmcd).
На основе параметров передаточной функции ОУ построим логарифмическую амплитудно-частотную характеристику (ЛАЧХ) статической части объекта управления (рисунок 3.1).
Рисунок 3.1 – ЛАЧХ статической части объекта управления
Построение графика ЛАЧХ необходимо для уточнения параметров расчёта:
начальной частоты расчета 0=0,01;
числа точек в пределах декады Nt=100;
числа декад варьирования частоты Nd=4.
Для изменения управляющего воздействия подаваемого на объект управления воспользуемся ПИД-регулятором.
Такой
регулятор является астатическим и имеет
три параметра настройки: коэффициент
усиления
,
время дифференцирования
и время интегрирования (или изодрома)
.
Передаточная функция ПИД-регулятора
обычно имеет вид:
.
(3.1)
При
использовании метода МП-разбиения
удобней, осуществив переобозначения
;
и
,
получить другое представление передаточной
функции
,
(3.2)
которое
используется в дальнейших расчётах.
Здесь постоянные коэффициенты
(
)
рассматриваются как псевдо настроечные
параметры регулятора и легко пересчитываются
в действительные настройки.
При
изменении параметра настройки
дифференциальной составляющей ПИД-закона
регулирования
меняются
области модально-параметрического
разбиения для настроек
и
.
Необходимо найти оптимальные значения
настроек в этих областях.
Прежде чем находить ПИД-закон регулирования, попытаемся найти области МП-разбиения для более простого ПИ-закона регулирования. Однако использование ПИ-регулятора приводит к необходимости ослабления ограничения на быстродействие. На рисунке 3.2 представлен вариант расположения фигуративных линий параметрического разбиения плоскости - параметров ПИ-закона управления.
Рисунок
3.2 – Вариант начального расположения
фигуративных линий параметрического
разбиения плоскости
-
параметров ПИ-закона (
).
Значения настроек:
,
Здесь
кривая 1 (красный цвет линии) представляет
собой параметрическую кривую D-разбиения,
отделяющую зону устойчивости; кривая
2 (синий цвет линии) – это параметрическая
кривая настройки регулятора для заданной
интенсивности затухания (граница степени
устойчивости
);
кривая 3 (зелёный цвет линии) – это
параметрическая кривая настройки
регулятора на заданную колебательность
(степень затухания колебаний
).
Из рисунка 3.2 видно, что САУ может иметь зону устойчивости для положительных и . Рассмотрим её ближе (рисунок 3.3).
Рисунок
3.3 – Вариант начального расположения
фигуративных линий параметрического
разбиения плоскости
-
параметров ПИ-закона (
).
Значения настроек:
,
.
Область положительных
-
Из рисунка 3.3 видно, что заданные параметры не являются оптимальными. Следовательно необходимо продолжить исследования.
Экспериментальным
путём были получены оптимальные значения
,
для ПИ-закона управления
.
На
рисунке 3.4 представлен вариант расположения
фигуративных линий параметрического
разбиения плоскости С1-С0
параметров ПИ-закона управления при
оптимальных
и
.
Рисунок
3.4 – Расположение фигуративных линий
параметрического разбиения плоскости
-
параметров
ПИ-закона регулирования. Значения
настроек:
,
.
Найденное
с представляет собой критическое
значение времени регулирования, то есть
это предельное минимальное время
регулирование при законе регулирования
с меньшими возможностями. Данное значение
не удовлетворяет значению быстродействия,
заданному в требованиях к системе.
Оптимизируем значение
за счёт применения ПИД-закона регулирования.
3.3. Выбор настроечных параметров
Выбирая на плоскости - точки, принадлежащие всем построенным параметрическим областям допустимых значений, получаем параметры настройки ПИД-регулятора в виде троек , , .
Путём
опытного подбора было выбрано начальное
значение
.
Для проверки правильности полученных
результатов, а также поиска наилучшего
поварьируем значения
и построим для каждого значения по 5
точек переходного процесса в синтезированной
системе (рисунки 3.5 – 3.7), определим
показатели её качества. Проверка
осуществляется с использованием ППП
Classic
(файл 3SZU.MDL
прилагается). Результаты представлены
в таблицах 3.1-3.3.
Рисунок
3.5 - Вариант расположения фигуративных
линий параметрического разбиения
плоскости
-
параметров ПИД – закона регулирования
при
.
Значения настроек:
,
.
Таблица 3.1 – Показатели качества ПИД – закона управления при С2=2
№ п/п |
с0 |
с1 |
с2 |
Перерегулирование ф, % |
Время регулирования tр, c |
1 |
1.26 |
3.2 |
2 |
10.58 |
3.3702 |
2 |
1.32 |
3.55 |
2 |
12.15 |
3.1855 |
3 |
1.42 |
3.25 |
2 |
12.68 |
3.5583 |
4 |
1.48 |
3.45 |
2 |
13.78 |
3.4231 |
5 |
1.56 |
3.2 |
2 |
14.35 |
3.7107 |
Рисунок
3.6 - Вариант расположения фигуративных
линий параметрического разбиения
плоскости С1-С0
параметров ПИД – закона регулирования
при
.
Значения настроек:
,
.
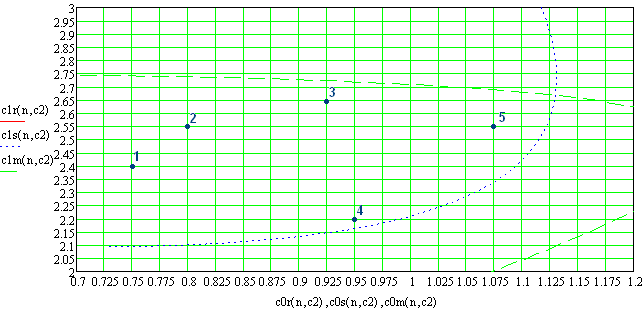
Таблица 3.2 – Показатели качества ПИД – закона управления при С2=1,5
№ п/п |
с0 |
с1 |
с2 |
Перерегулирование ф, % |
Время регулирования tр, c |
1 |
0.75 |
2.4 |
1.5 |
5.44 |
3.0798 |
2 |
0.8 |
2.55 |
1.5 |
6.98 |
3.2664 |
3 |
0.925 |
2.65 |
1.5 |
9.73 |
3.5686 |
4 |
0.95 |
2.2 |
1.5 |
9.64 |
4.4153 |
5 |
1.075 |
2.55 |
1.5 |
12.39 |
4.0132 |
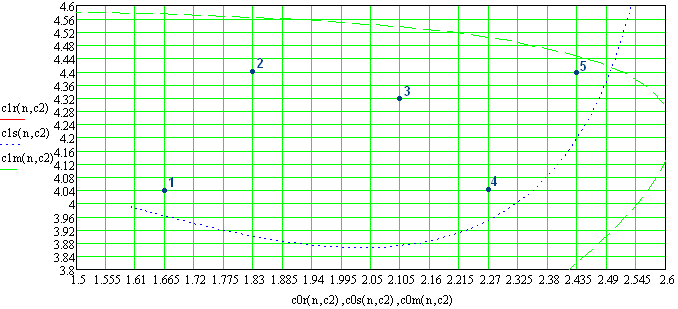
Рисунок
3.7 - Вариант расположения фигуративных
линий параметрического разбиения
плоскости С1-С0
параметров ПИД – закона регулирования
при
.
Значения настроек:
,
.
Таблица 3.3 – Показатели качества ПИД – закона управления при С2=2,5
№ п/п |
с0 |
с1 |
с2 |
Перерегулирование ф, % |
Время регулирования tр, c |
1 |
1.665 |
4.04 |
2.5 |
11.83 |
3.026 |
2 |
1.83 |
4.4 |
2.5 |
14.00 |
2.9595 |
3 |
2.105 |
4.32 |
2.5 |
15.97 |
3.1154 |
4 |
2.27 |
4.04 |
2.5 |
16.91 |
3.3517 |
5 |
2.435 |
4.4 |
2.5 |
18.55 |
3.1809 |
Сравним полученные показатели качества (таблица 3.4).
Таблица 3.4 – Показатели качества ПИД – закона управления при различных
№ п/п |
с0 |
с1 |
с2 |
Перерегулирование ф, % |
Время регулирования tр, c |
1 |
0.75 |
2.4 |
1.5 |
6.44 |
3.0798 |
2 |
0.8 |
2.55 |
1.5 |
6.98 |
3.2664 |
3 |
0.925 |
2.65 |
1.5 |
9.73 |
3.5686 |
4 |
0.95 |
2.2 |
1.5 |
9.64 |
4.4153 |
5 |
1.075 |
2.55 |
1.5 |
12.39 |
4.0132 |
1 |
1.26 |
3.2 |
2 |
10.58 |
3.3702 |
2 |
1.32 |
3.55 |
2 |
12.15 |
3.1855 |
3 |
1.42 |
3.25 |
2 |
12.68 |
3.5583 |
4 |
1.48 |
3.45 |
2 |
13.78 |
3.4231 |
5 |
1.56 |
3.2 |
2 |
14.35 |
3.7107 |
1 |
1.665 |
4.04 |
2.5 |
11.83 |
3.026 |
2 |
1.83 |
4.4 |
2.5 |
14.00 |
2.9595 |
3 |
2.105 |
4.32 |
2.5 |
15.97 |
3.1154 |
4 |
2.27 |
4.04 |
2.5 |
16.91 |
3.3517 |
5 |
2.435 |
4.4 |
2.5 |
18.55 |
3.1809 |
Из
таблицы 3.4 можно сделать вывод о том,
что лучшими показателями качества по
сравнению с другими выбранными точками
обладает точка имеющая показатели:
,
,
.
Соответственно действительные настройки
имеют вид:
,
,
.
ПИД-регулятор подключается к объекту управления согласно типовой схеме регулирования по отклонению, представленной на рисунке 3.8.
Рисунок 3.8 – Схема регулирования по отклонению
Передаточная функция ПИД – регулятора, полученная путём подстановки значений в формулу (3.2):
Переходный процесс в синтезированной системе показан на рисунке 3.9.
Рисунок 3.6 – Переходный процесс в синтезированной системе
Показатели качества синтезированной САУ имеют значения:
время регулирования, исходя из 5 %-трубки регулирования, tр = 3.2664 с;
перерегулирование ф = 6.95 %.
Таким образом, в результате синтеза ПИД – закона управления были получены параметры регулятора, удовлетворяющие поставленным критериям и улучшающие ранее полученный результат.