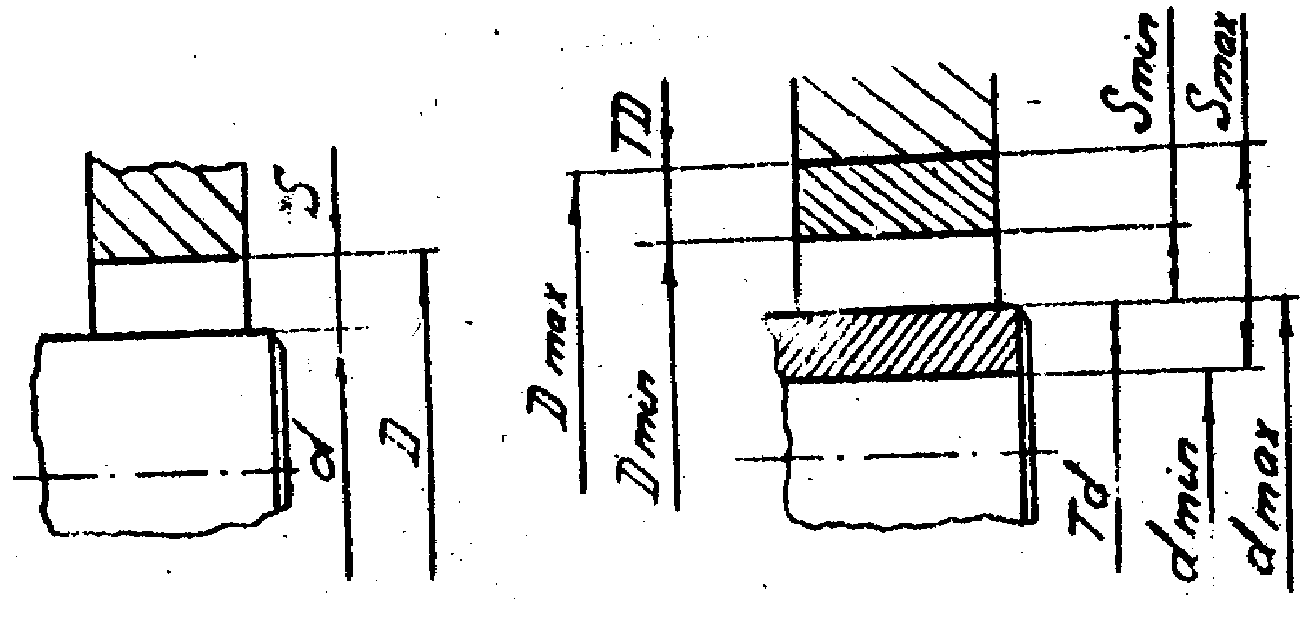
Посадки с зазором

Посадка с зазором это посадка, при которой обеспечивается зазор в соединении.

Поле допуска отверстия расположено над полем допуска вала.

Зазор - разность размеров отверстия и вала, если размер отверстия больше размера вала.

Рисунок 3

Размеры отверстия и вала в соединении колеблются в пределах допуска, следовательно и . зазор в соединениях будут изменяться от наибольшего до наименьшего значения; Smax = Dmax  dmin; Smax = Dmin  dmax Разность между наибольшим и наименьшим зазорами в соединении определяет допустимое изменение зазоров в годных соединениях или допуск посадки.

Допуск посадки численно равен сумме допусков отверстия и вала, составляющих соединение.

TS = S_max  S_min = TD +Td.

Посадки с натягом

Посадка с натягом это посадка, • при которой обеспечивается натяг в соединении.

Поле допуска отверстия расположено под полем допуска вала.

Натяг - разность размеров вала и отверстия до сборки, если размер вала больше размера отверстия.

Рисунок 4

Изза неизбежной неточности изготовления деталей необходимо задавать допустимые отклонения размеров вала и отверстия и этим допустить колебание натягов в соединениях от наибольшего до наименьшего значения Nmax = dmax  Dmin; Nmax =dmin  Dmax

Разность между наибольшим и наименьшим натягами определяет допустимое изменение натягов в годных соединениях, т.е. допуск посадки.

Допуск посадки с натягом TN = N_max  N_min = TD +Td.

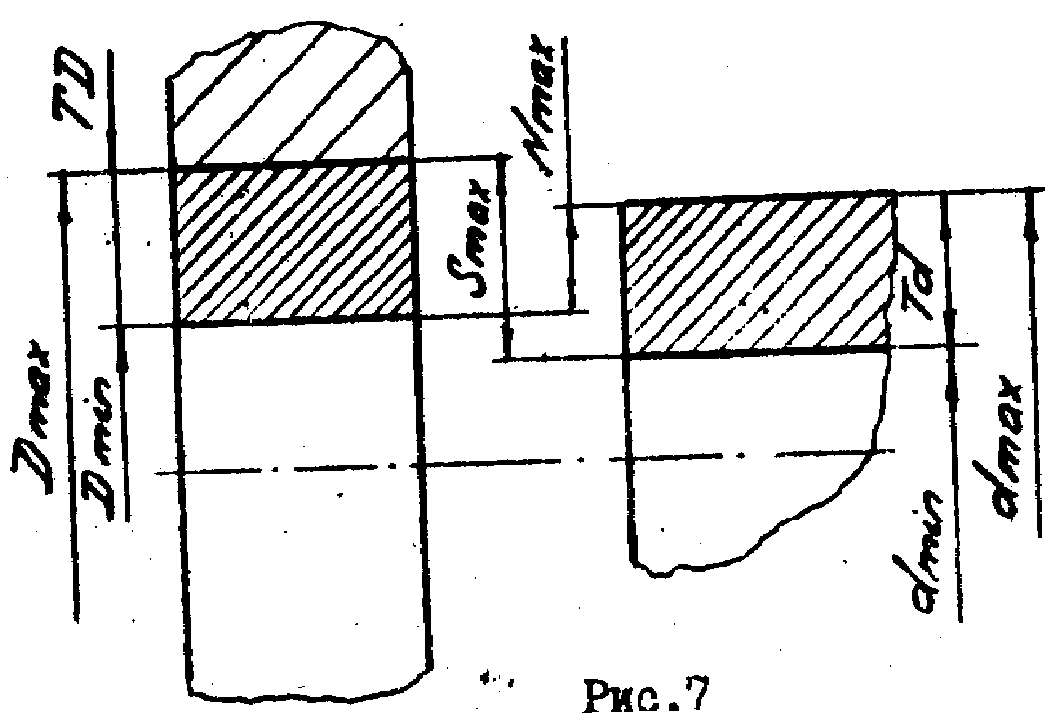
Переходные посадки.

Рисунок 5

Переходная посадка это посадка, при, которой возможно получение, как зазора, так и натяга. Nmax = dmax  Dmin; Smax = Dmax  dmin Поля допусков отверстия и вала расположены так, что перекрываются частично или полностью.

Допуск переходной посадки - это допустимое изменение зазоров и натягов в. годных соединениях.

Допуск переходной посадки T(S,N) = S_max + N_max = TD +Td.

Если допуск размера определяет точность размера, то допуск посадки определяет точность сопряжения.

Пример выполнения заданий.

Пример № 1.

Каким стандартным полям допусков соответствуют предельные отклонения размеров:

d =236

Основное отклонение 0,420мм = 420 мкм, что соответствует отклонению  b, для вала входящего в диапазон св.225 до 250 мм.

es = 420 мкм,

ei = 605 мкм.

Td = es  ei =420  ( 605) = 185 мкм, для диапазон размеров св. 180 до 250 этот допуск соответствует 10 квалитету.

d =236 , что соответствует стандартному полю допуска 236 b 10.

Пример №2

Каким стандартным полям допусков соответствуют предельные отклонения размеров. Для сопряжения указать характер посадки, в какой системе она выполнена. Сделать графическое изображение полей допусков сопрягаемых деталей.

38

Из этой записи видно, что сопряжение состоит из отверстия 38 и вала 38 .

Найдем, каким стандартным полям допусков соответствуют эти допуски.

Отверстие 38

Основное отклонение 25 мкм, что для отверстия входящего в диапазон св.30 до 40 мм.

соответствует отклонению  F,

ES = 125 мкм,

EI = 25 мкм.

Td = ESEI = 125  25 = 100 мкм, для диапазон размеров св. 30 до 50 мм этот допуск соответствует 10 квалитету.

D = 38 что соответствует стандартному полю допуска 38F10.

вала 38

Основное отклонение 9 мкм, что соответствует отклонению  g, для вала входящего в диапазон св.30 до 40 мм.

es = 9 мкм,

ei = 71 мкм.

Td = es  ei = 9  (71) = 62 мкм, для диапазон размеров св. 30 до 50 этот допуск соответствует 9 квалитету.

d

+125

=38 , что соответствует стандартному полю допуска 38g9.

TD

П

+ 25

0

0

мкм

осадка 38 , может быть записана 38

9

П

Td

осадка с зазором, в системе вала.

S_max = ES  ei = 125  (71) =196мкм

71

 38

S_min= EI  es = 25  ( 9 ) = 34 мкм

Пример № 3

По известным стандартным полям допусков указать: величину поля допуска; отклонения верхнее (es;ES), нижнее (EI;ei) , основное; предельные значения размеров;

d = 290k5

5 квалитету на размере 290 мм соответствует поле допуска Td = 23 мкм,

Для основного отклонения  k, на размере 290 мм и

5 квалитетом, т.е. входящим в интервал от 4 до 7 соответствует

числовое значение + 4 мкм это отклонение ei.

+27

T

Td

d =es ei es = ei + Td = 4 +23 = 27 мкм,

+4

d_max = d_H +es = 290 +0,027 =290,027 мм

0

0

d _min = d_H +ei = 290 + 0,004 =290,004 мм

 290

Пример № 4

По известным стандартным полям допусков указать: величину поля допуска; отклонения верхнее (es;ES), нижнее (EI;ei) , основное; предельные значения размеров;

d = 26j_s9

9 квалитету на размере 26 мм соответствует поле допуска Td = 52 мкм,

Д

+26

ля поля допуска  j_s отклонения считаются как симметричные относительно номинальной линии и равные половине поля допуска, т.о.

Td

es = Td / 2 = 52 / 2 = 26 мкм,

0

ei.= Td / 2 = 52 / 2 = 26 мкм,

d

0

_max = d_H +es = 26 +0,026 =26,026 мм

d

26

 26

_min = d_H +ei = 26 + (0,026) =25,974 мм

Расчет допусков размеров входящих в размерные цепи.

Основные термины и определения.

Сборка без пригонки не может быть обеспечена только за счет взаимозаменяемости деталей в отдельных сопряжениях (цилиндрических, конических, резьбовых, шлицевых и др.). Она будет достигнута лишь при одновременном выполнении заданных на сборочные единицы или изделие технических требований. Обеспечение точностных технических требований обычно достигается выявлением и расчетом размерных цепей (ГОСТ 16319—80, ГОСТ 16320—80).

Размерная цепь — совокупность размеров, непосредственно участвующих в решении поставленной задачи и образующих замкнутый контур.

Задачей может являться:

 обеспечение точности при конструировании изделия - конструкторская размерная цепь,

 обеспечение точности при изготовлении отдельных составных частей или деталей изделия - технологическая размерная цепь,

 измерение величин, характеризующих точность изделия -измерительная размерная цепь,

 обеспечение собираемости узла из составляющих деталей и узлов - сборочная размерная цепь.

Технологические цепи типичны при расчете положения поверхностей, осей и припусков под механическую обработку у отдельных деталей.

Размеры, образующие цепь, называют звеньями.

В зависимости от вида звеньев различают:

• линейные размерные цепи (звенья — линейные размеры),

• угловые (звенья — угловые размеры)

• смешанные.

В зависимости от расположения звеньев различают

 плоские размерные цепи - звенья расположены в одной или нескольких параллельных плоскостях,

 пространственные размерные цепи - часть или все звенья расположены в непараллельных плоскостях.

Звенья каждой линейной размерной цепи обозначают какой-либо одной прописной буквой русского алфавита с соответствующим числовым индексом, звенья угловых цепей -- строчной буквой греческого алфавита с индексом.

Отдельные звенья размерных цепей могут иметь номиналы, равные нулю. Например различные биения, начальные значения параллельности, соосности, иногда номиналы зазоров или натягов, температурные или упругие деформации.

Любая размерная цепь состоит из составляющих звеньев и одного замыкающего. Все составляющие звенья функционально связаны с замыкающим звеном.

Замыкающим звеном - называют звено размерной цепи, являющееся исходным при постановке задачи или получающееся последним в результате ее решения.

Размер замыкающего звена в процессе обработки или сборки получается как следствие обеспечения заданной точности каждого из составляющих звеньев. Следовательно, замыкающее звено в размерной цепи является самым мало точным, так как его погрешность суммируется из погрешностей остальных размеров. Поэтому при выявлении размерных цепей необходимо стремиться составлять их из минимально необходимого числа звеньев.

Составляющие звенья разделяются на увеличивающие и уменьшающие.

Увеличивающими звеньями называют те, с увеличением которых замыкающее звено увеличивается, а уменьшающими — те, с увеличением которых замыкающее звено уменьшается.

Выявленные в механизме или на детали размерные цепи часто недостаточно наглядны, поскольку размеры звеньев могут быть разбросаны по чертежу, порой на разных разрезах и сечениях. Поэтому для удобства решения составляют схему размерной цепи, представляющую ее графическое безмасштабное изображение (рисунок 1).

Рисунок 1

Для безошибочного определения увеличивающих и уменьшающих звеньев над буквенным обозначением замыкающего звена рекомендуется ставить штриховую стрелку острием влево, а затем над всеми составляющими звеньями стрелки проставляют так, как если бы они показывали принятое направление движения в замкнутом контуре цепи потока какой-либо среды.

Звенья, направление стрелок которых совпадает с направлением стрелки замыкающего звена (влево), являются уменьшающими; звенья со стрелками, направленными в противоположную сторону (вправо), являются увеличивающими.

Размерные цепи используют для решения двух типов задач прямой и обратной. Прямая задача заключается в назначении номиналов и полей допусков составляющих звеньев по известным (заданным) предельным размерам замыкающего звена Номиналы составляющих звеньев, как правило, назначают предварительно на основе расчетов либо из конструктивных соображений. Прямые задачи типичны при решении конструкторских размерных цепей.

Обратная задача заключается в определении номинала и предельных отклонений замыкающего звена по известным номиналам и предельным отклонениям составляющих звеньев. Обратная задача, в частности, позволяет проверить правильность решения прямой задачи

Размерные цепи можно решать несколькими методами (ГОСТ 16320—80):

1. Полной взаимозаменяемости (метод максимума—минимума), требуемая точность замыкающего звена размерной цепи достигается у всех без исключения объектов при включении в нее составляющих звеньев без выбора, подбора или какой-либо подгонки. Метод исходит из предположения, что в одной размерной цепи одновременно могут оказаться все звенья с предельными значениями, причем в любом из двух наиболее неблагоприятных сочетаний. Все увеличивающие звенья с верхними предельными размерами, а уменьшающие — с нижними или наоборот.

2. Неполной взаимозаменяемости (вероятностный метод), требуемая точность замыкающего звена размерной цепи в условиях беспригоночной сборки достигается не у всех объектов, а лишь у достаточно большой заранее обусловленной их части. Этот метод применяют, когда экономически целесообразно назначать более широкие допуски на составляющие звенья в предположении, что их действительные размеры будут группироваться в более узких пределах по одному из вероятностных законов, и процент риска выхода отклонений замыкающего звена за пределы поля допуска не превысит заранее принятого значения.

3. Решение высокоточных конструкторских цепей возможно путем введения в их состав звена-компенсатора. Если для достижения требуемой точности замыкающего звена с компенсатора каждого объекта удаляют излишний в данном случае слой материала, то это метод пригонки. Если предусмотрена возможность изменять действительный размер компенсатора без снятия материала, т.е. путем подбора деталей из ряда заранее изготовленных либо перемещением с последующей фиксацией, то это метод регулирования.

4. Возможно также применение метода групповой взаимозаменяемости, при котором точность замыкающего звена достигается за счет включения в размерную цепь отдельных составляющих звеньев, предварительно рассортированных по действительным размерам на группы.

Решение плоских размерных цепей по методу полной взаимозаменяемости.

Рассмотрим основные соотношения и порядок расчета линейных размерных цепей с параллельными звеньями по методу полной взаимозаменяемости. Понятнее и проще начать ознакомление с обратной задачи. Для решения размерных цепей используют ряд расчетных формул.

Первая формула условно может быть названа уравнением номиналов. Номинальный размер замыкающего звена размерной цепи равен

= ( 1 )

где т — общее число звеньев в размерной цепи, включая замыкающее; j— номер составляющего звена; ξ — передаточное отношение j-го звена размерной цепи.

Передаточное отношение отражает характер составляющего звена (увеличивающие звенья имеют знак плюс, уменьшающие — минус) и степень влияния отклонений данного j-го составляющего звена на отклонения замыкающего звена. Для цепей с параллельными звеньями передаточное отношение равно либо +1, либо —1.

Если рассматривать только цепи с параллельным звеньями. Тогда формулу (1) можно записать в развернутом виде, из которого следует, что номинал замыкающего звена равен разности сумм номиналов увеличивающих и уменьшающих размеров:

=  , ( 2 )

где п и р— число соответственно увеличивающих и уменьшающих звеньев в размерной цепи, т. е.

(п + р) = т—1; (3)

Формулы для определения предельных отклонений за мыкающего звена верхнего и нижнего могут быть названы  уравнениями отклонений. Предельные отклонения замыкающего звена в рассматриваемом случае наиболее удобно и быстро определять по зависимостям, включающим верхние Es_j и нижние Ei_j предельные отклонения составляющих звеньев:

(4)

=  ,

=  .

Тогда предельные размеры замыкающего звена определятся как алгебраическая сумма номинального размера и предельных отклонений:

_max = + , _min = + ; ( 5)

Уравнение допусков устанавливает, что допуск замыкающего звена при расчете размерной цепи по методу полной взаимозаменяемости равен сумме допусков всех составляющих звеньев:

T_ = ; (6)

Решение прямой задачи слагается из нескольких этапов:

1. Производят необходимые подготовительные действия, включающие:

• выявление замыкающего и составляющих звеньев размерной цепи,

• изображение размерной схемы,

• разделение составляющих звеньев на увеличивающие и уменьшающие,

• проверку правильности назначения номиналов составляющих звеньев по уравнению (1)

2. Определяют среднюю точность составляющих звеньев размерной цепи, исключая размеры стандартизованных звеньев (например, подшипников качения).

Среднюю точность размерной цепи можно определить по среднему числу единиц допуска a_m , приходящихся на одно составляющее звено, исключается стандартизованные детали:

a _m = T_ ; (7)

где i_j  значение единицы допуска ( см. приложение 6) для каждого не стандартизованного звена. T_{ } исходный допуск замыкающего звена, за вычетом суммы допусков стандартизованных деталей.

Существует способ назначения равных допусков, при котором допуск исходного звена делят поровну на все составляющие звенья цепи. Он пригоден только в случае примерно равных значений номиналов составляющих звеньев, либо для быстрой предварительной прикидки среднего значения искомых допусков в целях определения их приемлемости и последующей корректировки на основе технико-экономических соображений

При получении значения Td, близкого к середине между двумя соседними значениями в квалитетах, часть звеньев задают по ближайшему более точному, а часть — по ближайшему более грубому квалитету с учетом ответственности звеньев и сложности их обработки.

3. С учетом найденного среднего квалитета на составляющие звенья назначают стандартные поля допусков.

4. Согласовывают получающийся суммарный допуск всех составляющих звеньев с допуском замыкающего звена.

5. Проверяют предельные отклонения замыкающего звена решением обратной задачи и, при необходимости, корректируют отклонения (а иногда и номинал) одного из составляющих звеньев.

При назначении на составляющие звенья полей допусков следует стремиться преимущественно использовать поля допусков основных деталей (H или h), направленных «в тело». Когда вопрос так решить затруднительно, допуски задают с симметричным отклонением.

Во всех случаях следует стремиться полученные по расчету нестандартные отклонения заменить близкими стандартными при условии обеспечения или некоторого ужесточения получающихся при этом параметров замыкающего звена против заданных.

Решение размерных цепей методами пригонки и регулирования.

Сущность методов состоит в том, что при получении в результате расчета средней точности у составляющих звеньев излишне жестких допусков их расширяют, назначая по экономически приемлемым квалитетам. Получающийся после этого у замыкающего звена избыток поля рассеяния при сборке устраняют за счет компенсатора. По конструкции компенсаторы бывают:

 подвижными (например, регулировочный клин в направляющих суппортов, перемещающаяся в продольном направлении втулка со стопорным устройством и др.),

 неподвижными.

Неподвижное компенсирующее звено в виде кольца или прокладки может быть специально предусмотрено в механизме, либо для указанной цели используют одну из удобных для пригонки «по месту» деталей изделия. Чтобы избежать поштучной пригонки, компенсаторы обычно подают на сборку в виде комплектов колец разной толщины либо получают необходимую в каждом отдельном случае толщину набором из нескольких одинаковых прокладок.

Если по технико  экономическим соображениям использование квалитетов для размеров рассчитанных по методу max min не приемлемо, следует ввести компенсирующее звено.

Индекс одного из составляющих звеньев заменяется на «к». Допуск на остальные составляющие звенья назначают исходя из экономических соображений. Допуск обычно располагается в «тело».

Допуск замыкающего звена расширяется, его рассчитывают по формуле:

T^’_ = ; (8)

где T_j  допуск всех составляющих звеньев кроме звена компенсатора.

Зная допуск замыкающего звена рассчитанный по методу max min (T_) и допуск рассчитанный по формуле (8) находим наибольшую величину компенсации:

V_к = T^’_  T_ ; (9)

Используя формулы (3) находятся отклонения замыкающего звена без учета компенсирующего звена.(E^’_SΔ; E^’_iΔ )

По расчету со штрихом заданным отклонениям замыкающего звена находится отклонение компенсирующего звена:

у

( 10 )

меньшающее звено: E^’_Sк =E^’_SΔ  E_SΔ ; E^’_iк = E^’_iΔ  E_iΔ

увеличивающее звено : E^’_Sк =E_iΔ  E^‘ _iΔ ; E^’_iк = E _SΔ  E^‘_SΔ

Исполнительный размер компенсатора определяют его наибольшей величиной с приемлемым допуском, так чтобы его наименьший размер был не менее необходимой наименьшей величины компенсатора.

Размер компенсатора, в который его надо обработать для каждого конкретного случая, определяют «по месту» после постановки в механизм или путем измерения действительных размеров остальных деталей, входящих в размерную цепь.

При использовании метода регулирования по наибольшей возможной компенсации V_к следует рассчитать число ступеней N неподвижных компенсаторов:

N = V_к /( T_ - Т_К), ( 11 )

где Т_К — допуск на изготовление компенсатора, назначаемый в этом случае минимальной экономически приемлемой величины.

Соответственно найденному числу ступеней получающийся широкий допуск T’_ замыкающего звена делят на такое же число зон. Определяя измерением в каждой сборке получившуюся зону, вставляют в механизм соответствующий ей неподвижный компенсатор (или набор из нескольких одинаковых компенсаторов).

Метод расчета на максимум—минимум применяют в случаях, когда необходима полная взаимозаменяемость, в штучных изделиях для относительно коротких цепей (до пяти звеньев), для ориентировочных расчетов (вследствие простоты), в грубых размерных цепях (когда допуск хотя бы одного звена очень большой), а также для технологических размерных цепей в единичном и серийном производствах. В остальных случаях правильнее применять расчеты по вероятностному методу.

Применение теории вероятности к расчету допусков в размерных цепях.

При изготовлении деталей имеет место рассеяние их действительных размеров под воздействием случайных и систематических причин.

Случайные причины  непостоянство припусков и твердости заготовок и т. п.  приводят к колебанию упругого деформации системы станок—приспособление—инструмент—деталь. Влияние случайных причин в результате совершенства заготовок, приспособлений и других элементов технологического процесса в определенной мере может быть уменьшено, но полностью их устранить невозможно.

Переменные систематические причины (например, изменения размера режущего инструмента вследствие износа) усугубляют явление рассеяния.

Постоянные систематические причины ошибки в расположении приспособления, погрешности его установочных или направляющих элементов, отдельные погрешности станка и инструментов не влияют на закон распределения размеров, а лишь приводят к смещению центра группирования.

В отлаженном установившемся производстве доминирующими являются случайные причины, поэтому полагают, что рассеяние действительных размеров в этих случаях происходит по закону нормального распределения. Это значит, что на сборку поступает деталей со средними размерами много больше, чем с близкими к предельным, и колебание размера замыкающего звена под влиянием полей рассеяния составляющих звеньев будет происходит в заметно меньшей степени, чем это получается порасчету на максимум—минимум. Следовательно, вероятностный метод расчета позволяет значительно расширить допуски составляющих звеньев при одном и том же заданном допуске замыкающего звена, что упрощает и удешевляет производство.

Используя предельные теоремы теории вероятностей допуск замыкающего звена T_ определяют путем квадратичного суммирования допусков составляющих звеньев с учетом закона их распределения:

T_ = t_ ; ( 12 ) где t_ — коэффициент риска, —- относительное среднеквадратическое отклонение,

для цепей с параллельными звеньями = 1.

В зависимости от принимаемого процента риска Р при совпадении центра группирования с координатой центра отклонений для нормального закона распределения и равновероятного выхода за обе границы поля допуска значение t_ выбирают из ряда:

Р, %	32	10	4,5	1,0	0,27	0,1	0,01
t	1,00	1,65	2.00	2,57	3,00	3,29	3,89

Относительное среднеквадратическое отклонение при расчетах на стадии проектирования принимают, исходя из предполагаемого закона распределения:

= 1/3, если при расчете неизвестен характер кривой рассеяния размеров  для изделий мелкосерийного и индивидуального производства;

= 1/6, если предполагается, что рассеяние размеров близко к закону равнобедренного треугольника Симпсона;

= 1/9, если предполагается, что кривая рассеяния будет иметь нормальный (Гаусса) характер  для изделий массового и крупносерийного производства.

Часто пользуются коэффициентом относительного рассеяния K_j,. Он связан со стандартным показателем соотношением

K_j = t_ ; ( 13 )

.  При наиболее употребительном проценте риска 0,27 (t_= 3) значения коэффициента относительного рассеяния K_j составляют 1при законе распределения Гаусса;

 при проценте риска 1,22 K_j² = 1,5  для закона Симпсона;

 при проценте риска 1,73 K_j² = 3  для неизвестного закона распределения. Формула (12) приобретает более простой вид:

T_ = ; ( 14 )

Координата середины поля допуска замыкающего звена:

E_CΔ = ; ( 15 )

где E_cj — координата середины поля допуска ; j-го составляющего звена, подсчитываемая по его предельным отклонениям.

Ec_j = 0,5 (Es_j + Ei_j); ( 16 )

Тогда предельные отклонения замыкающего звена могут быть найдены по соотношениям:

Es_Δ = Ec_Δ + 0,5T_Δ ; Ei_Δ = Ec_Δ  0,5T_Δ (17)

При несимметричных законах распределения размеров составляющих звеньев следует определить центр группирования (математического ожидания) отклонений замыкающего звена Ет_Δ В общем случае

Ет_Δ = ; ( 18 )

где Ecv_j — координата середины поля рассеяния j-го звена (при совпадении поля рассеяния с полем допуска Ecv_j = Еc_j; и рассеяние равно допуску: V_j = Т_j); α_j — коэффициент относительной асимметрии j-го звена, равный отношению смещения (абсолютной асимметрии) координаты центра группирования кривой распределения Ет_j от координаты

Ecvj Emj 0,5Tj 0,5Tj Vj=Tj Aj Рисунок 2

середины поля допуска Еcj к половине величины допуска (рисунок 2): αj = ; ( 19 )

При отсутствии конкретных данных о законах распределения размеров замыкающих звеньев (на стадии проектирования) значения α_j принимают ориентировочно . Методы расчета коэффициентов относительной асимметрии и относительного рассеяния замыкающих звеньев изложены в ГОСТ 19415—74.

При симметричном рассеянии размера замыкающего звена (α_Δ = 0) координата его середины поля рассеяния равна величине координаты центра группирования:

Ecv_Δ= Em_Δ .

При решении прямой задачи вероятностным методом формула для определения среднего квалитета звеньев цепи по смыслу подобна формуле ( 7 ), но имеет другой вид:

a_m = ; ( 20 )

Кроме уже рассмотренных методов как при полной, так и не полной взаимозаменяемости может быть применен способ пробных расчетов, при котором допуски на составляющие размеры назначают экономически целесообразными с учетом вида производства, конструктивных требований, опыта эксплуатации подобных механизмов и проверенных для данного производства значений коэффициентов K_j и α_j. Приемлемость назначенных полей допусков проверяют сначала на суммарное влияние по формуле ( 6 ) или (12) с корректировкой их величины в случае необходимости, а затем по предельным отклонениям замыкающего звена по формуле ( 4) или (17).

Прложение №1

Интервалы номинальных размеров в мм

(ГОСТ 2534688)

Основные интервлы		Промежуточные интервалы
Свыше	До	Свыше	До
	3		
3	6		
6	10		
10	18	10	14
		14	18
18	30	18	24
		24	30
30	50	30	40
		40	50
50	80	50	65
		65	80
80	120	80	100
		100	120
120	180	120	140
		140	160
		160	180
180	250	180	200
		200	225
		225	250
250	315	250	280
		280	315
315	400	315	355
		355	400
400	500	400	450
		450	500

Приложение № 2

Отностельное положене полей допусков.

(ГОСТ 2534688)

Приложение № 5

Значение полей допусков для квалитетов.

(ГОСТ 2534688)