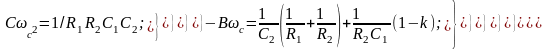3. Проектирование аф нижних частот

3.1. Схемная реализация фнч Баттерворта и Чебышева

Существует несколько способов построения активных ФНЧ Баттерворта и Чебышева: с многопетлевой обратной связью, на источниках напряжения, управляемых напряжением (ИНУН), биквадратный ФНЧ и др. Ввиду ограниченного объема работы будем рассматривать первые две схемы. Методика расчета других схем ФНЧ приводится в [3].

Как было отмечено выше, основу фильтров с порядком n>2 составляют фильтры 2-го и 1-го порядков, соединенные каскадно. Поэтому ниже приведена методика расчета ФНЧ 2-го и 1-го порядков.

3.1.1. Фнч 2-го порядка с многопетлевой обратной связью

Для ФНЧ 2-го порядка с заданной частотой среза ω_c типовая полиномиальная передаточная функция имеет вид:

(3.1)

где B и C – нормированные коэффициенты, поскольку для ω_c =2πf_В= 1 рад/с данная передаточная функция при n=2 приводится к виду (2.7). Для фильтров Баттерворта и Чебышева значения нормированных коэффициентов B и C приведены в приложении 1. Постоянная k определяет коэффициент усиления фильтра, который должен быть предварительно задан.

Одной из наиболее простых схем АФ, реализующих передаточную функцию ФНЧ 2-го порядка согласно (3.1), является схема с многопетлевой обратной связью (МОС) (рис. 3.1). Схема имеет такое название потому, что она содержит два пути прохождения сигнала обратной связи через элементы C₁ и R₂.

Рис. 3.1. ФНЧ 2-го порядка с МОС

Эта схема реализует уравнение (3.1) с инвертирующим коэффициентом усиления и параметрами:

(3.2)

Номинальное значение емкости C₂ задается близким к величине  Ф. Значение емкости C₁ выбираем из условия:

(3.3)

Номиналы резисторов рассчитываются по формулам:

(3.4)

Чем выше порядок ФНЧ, тем более критичными являются требования приближения номинальных значений резисторов и конденсаторов к расчетным.

Фильтр с МОС является наиболее простым и может широко применяться для реализации фильтров с инвертирующим коэффициентом усиления. Он имеет хорошую стабильность характеристик, низкое выходное сопротивление. Недостатком схемы является то, что её целесообразно применять для значений коэффициента усиления k и добротности Q, не превышающей 10. Если Q много меньше 10, то значение k может быть большим при выполнении условия kQ=100.

3.1.2. Фнч 2-го порядка на инун

На рис. 3.2 изображена широко распространенная схема ФНЧ 2-го порядка, реализующая неинвертирующий (положительный) коэффициент усиления.

Рис. 3.2. ФНЧ 2-го порядка на ИНУН

Эта схема называется фильтром на ИНУН, поскольку ОУ и два подсоединенных к нему резистора R₃ и R₄ образуют источник напряжения, управляемый напряжением. Схема реализует функцию ФНЧ (3.1) с неинвертирующим коэффициентом усиления вида (3.1) с параметрами:

(3.5)

Значения резисторов рассчитываются по формулам:

(3.6)

Коэффициенты k, B, C определяются аналогично схеме с МОС, описанной выше. Если k = 1, то R₁ и R₂ также определяются из (3.6), и в этом случае получаем R₃ = ∞ (разомкнутая цепь), а R₄ = R₁ + R₂. В большинстве случаев при k = 1 значение R₄ принимают равным нулю (короткозамкнутая цепь). Если k = 1, то ИНУН работает как повторитель напряжения. Номинальное значение емкости C₂ выбирается близким к значению  Ф, а значение емкости C₁ – из выражения:

(3.7)

Последовательность расчета ФНЧ на ИНУН аналогична расчету ФНЧ с МОС и приведена ниже.

Фильтр на ИНУН позволяет добиться неинвертирующего коэффициента усиления при малом числе элементов, он прост в настройке. Однако, подобно фильтру с МОС, фильтр на ИНУН должен использоваться при значениях добротности Q ≤ 10.