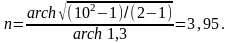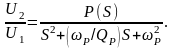2.3.2. Выбор минимального порядка фильтров

Чем выше порядок фильтра Чебышева или Баттерворта, тем лучше его АЧХ. Однако более высокий порядок усложняет схему и повышает сложность фильтра. Поэтому в процессе проектирования необходимо выбрать минимально необходимый порядок фильтра, удовлетворяющего заданным требованиям. Одним из основных показателей, которым должен удовлетворять АФ, является ширина переходной области Δf, которая определяется по формуле (см. рис. 2.2):

(2.16)

Для фильтра Баттерворта с a₁ = 3 дБ минимальный порядок фильтра можно определить из выражения:

(2.17)

где логарифмы могут быть десятичными, или натуральными.

Параметр Δf / f_В называется нормированной шириной переходной области и является безразмерной величиной. Следовательно, Δf и f_В можно задавать и в радианах в секунду, и в герцах.

Например, если a₁ = 3 дБ; a₂ = 20 дБ; f_В = 1000 Гц, а Δf = 300 Гц, то удовлетворяющий этим условиям фильтр Баттерворта должен иметь следующий минимальный порядок:

(2.18)

Поскольку порядок должен быть целым числом, то берем ближайшее целое число n = 9.

Минимальный порядок фильтра Чебышева определяется выражением:

(2.19)

Функцию гиперболического арккосинуса можно определить:

(2.20)

Например, если a₁ = 3 дБ; a₂ = 20 дБ; f_c = 1000 Гц, а TW = 300 Гц, то

(2.21)

Находя ближайшее целое число, получаем n = 4.

Рассмотренные два примера убеждают в преимуществе фильтра Чебышева перед фильтром Баттерворта, если основным параметром является АЧХ. В рассмотренном случае фильтр Чебышева обеспечивает ту же крутизну передаточной функции, что и фильтр Баттерворта удвоенной сложности. Уравнения (2.17) и (2.19) можно также использовать для нахождения ширины переходной области Δf фильтров Баттерворта и Чебышева фиксированного порядка.

Передаточная функция фильтров 1-го и 2-го порядков. Для фильтров 1-го порядка передаточная функция представляется в виде [3]:

(2.22)

где P(S) – полином первой или нулевой степени; C – постоянное число.

Для фильтров второго порядка передаточная функция

(2.23)

где P(S) – полином второй или меньшей степени; B и C– постоянные числа.

Для АФ четного порядка с n>2 обычная каскадная схема содержит звеньев 2-го порядка, каждое из которых имеет передаточную функцию вида (2.23). Если же порядок АФ с n>2 является нечетным, то схема содержит звеньев 2-го порядка с передаточными функциями типа (2.23) и одно звено 1-го порядка с передаточной функцией типа (2.22).

Для фильтров, описываемых (2.23), собственная частота ω_p и добротность Q_p определяются из соотношения [2]:

(2.24)

Уравнение (2.23) можно переписать в виде

(2.25)

Проектирование АФ с порядком n>2. Одним из основных методов проектирования АФ, у которых значение n>2, является каскадное соединение звеньев 1-го и 2-го порядков, что позволяет получить фильтр любого высокого порядка [4]. При каскадном соединении звеньев сумма порядков каждого звена равна порядку фильтра n:

(2.26)

где n_i – порядок i-го звена фильтра (i = 1,2,3,…).

Суммарный коэффициент передачи АФ равен произведению коэффициентов передачи исходных звеньев:

(2.27)

где k_i – коэффициент передачи i-го звена фильтра (i = 1,2,3,…).

Увеличивая число соединяемых фильтров 1-го и 2-го порядков, можно получить фильтр любого нужного нам порядка. Фильтры нечетных порядков обычно строятся из нескольких фильтров 2-го порядка в качестве первых каскадов и фильтра 1-го порядка в качестве последнего. Ввиду того, что каскадное соединение звеньев приводит к сужению полосы пропускания, не следует делать отдельные каскады многозвенных фильтров идентичными.

При построении каскада следует учитывать, что его звенья должны располагаться в порядке убывания коэффициента усиления:

(2.28)

Как видно на рис. 2.4, каскадное соединение фильтров 2-го и 1-го порядков дает фильтр 3-го порядка, каскадное соединение двух фильтров 2-го порядка дает фильтр 4-го порядка и т.д.

Рис. 2.4. Структурные схемы фильтров (1 – фильтры 1-го порядка;

2 – фильтры 2-го порядка

В многокаскадных полосовых АФ обычно используют четное число каскадов. Если ширина полосы пропускания полосового фильтра больше, чем (приблизительно) 50%, то такой полосовой фильтр проще построить из фильтра верхних и нижних частот, соединив эти два фильтра каскадно.