4.8. Автоматизированное нивелирование

Автоматическое нивелирование производится при помощи высотомеров-автоматов, позволяющих автоматически вычерчивать профиль линии местности или получать отметки точек этой линии. Высотомеры-автоматы бывают механические, электромеханические и электронно-механические. Все эти приборы монтируются на шасси, при перемещении которого по заданному направлению рисуется профиль местности.

Механический высотомер-автомат М.А. Артанова установлен на двухколесной тележке. Основой его частью является тяжелый маятник, который задает осевое перемежение ролику, фрикционно-связанному с диском. Диск, в свою очередь, связан с колесом тележки. Вращение диска, тем самым, будет пропорционально проходимому расстоянию. Вращательное движение ролика преобразуется в поступательное движение чертежного узла, вычерчивающего профиль местности. Ролик связан и со счетчиком превышений. Средняя квадратическая погрешность определения превышений составляет ± 0,15 м на 1 км хода.

Электрический высотомер-автомат типа ВА-1М или ВА-56 сконструирован с учетом ускорения движения тележки, и соответствующая компенсация маятника позволяет производить нивелирование при скорости движения до 30 км в час. Профиль местности фиксируется на фотопленке. Средняя квадратическая погрешность определения превышений составляет ± 0, 20 м на 10 км хода.

Электронно-механический высотомер-автомат АВА маятниковой системы аналогичен приборам ВА-1М и ВА-56. Схема прибора выполнена на полупроводниковых элементах, что позволяет существенным образом снизить вес и габариты прибора, повысить стабильность работы счетно-решающего узла. Прибор обеспечивает непрерывную запись профиля на фотопленке и визуальный отсчет превышений и расстояний по счетчикам.

4.9. Фотограмметрическое нивелирование

Фотограмметрическое нивелирование основано на возможности получения модели местности при обработке пары взаимно ориентированных фотоснимков земной поверхности. Получение модели местности возможно двумя способами: способом непосредственного построения модели на экране прибора и способом стереоскопического наблюдения пары взаимно ориентированных фотоснимков.

В первом случае используется свойство геометрической обратимости фотографического процесса, которое позволяет получать модель местности в лабораторных условиях.

Сущность геометрической обратимости фотографического процесса заключается в следующем.

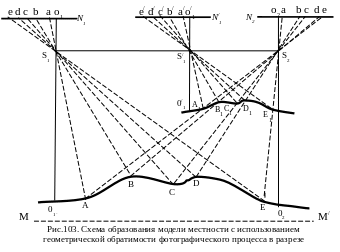
Допустим (рис. 103), имеется возможность восстановления момента фотографирования местности по линии ABCDE с двух точек базиса S₁ S₂. Из анализа рисунка видно, световые лучи от точек ABCDE местности, пройдя через центр проекции S₁ S₂, изобразятся на левом N₁ фотоизображении в точках e d c b a и на правом N₂ – в точках a b c d e. Если осветить полученные два фотоизображения, то световые лучи от их точек, пройдя центры проектирования, вернутся в исходные точки местности. Убрав на этом участке местность, ее точки и, следовательно, сама местность не исчезнут. Действительно, хотя местность отсутствует, но ее поверхность существует в результате пересечения световых лучей, идущих от одноименных точек фотоизображений.

В принципе полученную модель местности можно измерять. Однако практически это сделать невозможно, так как масштаб этой модели 1:1. Для воссоздания ее в лабораторных условиях необходимо центр проекции S₁ поступательно переместить в положение S^/₁ (рис. 103). Масштаб такой модели будет равен отношению базиса проектирования b = S^/₁S₂ к базису фотографирования В = S₁S₂

. (157)

Для наблюдения поверхности полученной модели А₁В₁С₁D₁Е₁ используется метод цветных анаглифов. Этот метод позволяет получать объемное изображение по двум окрашенным в дополнительные цвета изображениям, составляющих стереопару, рассматриваемых через разноокрашенные светофильтры (разноцветные очки).

Этот принцип получения модели местности положен в основу фотограмметрических приборов – мультиплексов, которые состоит из 9, 12 или 24 проекторов. Таким образом, мультиплекс позволяет в отличие от модели рис. 104 создавать модель местности на протяжении 8, 11 или 23 стереопар. Это достоинство мультиплексов несколько меркнет перед необходимостью в лабораторных условиях уменьшать габариты проекторов, использовать светофильтры, что приводит к потере точности результатов. Поэтому в настоящее время применяется второй способ – способ непосредственного наблюдения пары взаимно ориентированных фотоснимков, в результате чего возникает стереоэффект.

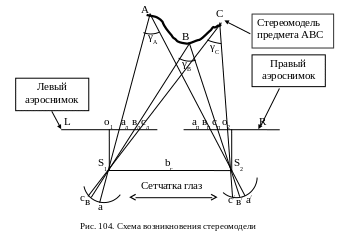
Стереоэффект – это свойство нервной системы при рассматривании двух плоских изображений одного и того же предмета получать одно объемное изображение предмета. Стереоэффект возникает тогда, когда два перекрывающихся фотоснимка взаимно ориентированы и рассматриваются раздельно: левым глазом левый L фотоснимок, а правым – правый R (рис. 104). При этом зрительные оси направляются на одноименные точки фотоснимков. В своем продолжении эти направления пересекутся, образуя стереомодель АВС данного предмета.

Получение стереоэффекта невооруженными глазами связано с некоторыми трудностями: во–первых, левое изображение предмета должно рассматриваться только левым глазом, а правое – только правым, во–вторых, расстояние между одноименными точками, например, а_ла_п (см. рис. 104) на взаимно ориентированных изображениях стереопары не должны превышать величину b_г глазного базиса. На практике и то и дру-гое соблюсти трудно. Поэтому получение стереоэффекта невооруженными глазами связано с напряжением зрения и возможно после длительной тренировки.

Чтобы облегчить получение стереоскопической модели местности, пользуются специальными наблюдательными системами, которые позво-ляют четко разделить наблюдаемые изображения и свести расстояния между наблюдаемыми одноименными точками левого и правого изображения до величины глазного базиса.

Простейшей такой системой является стереоскоп. Линзово-зеркаль-ный стереоскоп (рис. 105) состоит из двух пар зеркал и двух линз, смон-тированных на соединительной планке с четырьмя ножками.

Схема получения стереомодели показана на рис. 106. Изображение левого снимка (точек а, в и с), отразившись от большого и малого зеркал, попадает только в левый глаз, а изображение правого снимка (точек а^/, в^/ и с^/) через другую пару зеркал – в правый глаз. Стереоскопическая модель АВС возникает на продолжении зрительных лучей.

Сущность стереоскопического нивелирования объясняется той же геометрической обратимостью фотографического процесса (рис.107).

Допустим, что некоторая точка А местности имеет превышение АА_о над плоскостью Т, проходящей через точку 0₁, и при фотографировании с концов горизонтального базиса В изобразилась на паре горизонтальных аэроснимков в соответствующих точках а₁ и а₂. Анализ подобных треугольников S₁S₂A и А₂АА₁ показывает, что после соответствующих замен отрезков местности отрезками, измеренными на аэроснимках, искомая величина превышения будет равна

h = (158)

где - разность продольных параллаксов, измеренных для исходной (Р_исх) и определяемой (Р_i) точек аэроснимка, b – базис фотографирования в масштабе аэроснимка, Н – высота фотографирования, Р = х_А – х_А^/ - разность абсцисс, измеренных для одной и той же точки в системе координат соответственно левого и правого аэроснимков.

Таким образом, для определения превышения между двумя точками местности необходимо измерить на паре аэроснимков этой местности величины абсцисс для этих точек в системе координат левого и правого аэроснимков. Затем взять разность абсцисс для каждой точки, т.е. найти величины продольных параллаксов, учитывая, что положительное направление осей координат вверх у и вправо х. После этого вычислить разность продольных параллаксов и найти искомое превышение по формуле (158).

На практике величины абсцисс не измеряются, а определяются непосредственно параллаксы или в современных приборах превышения.

Принцип измерения по аэроснимкам непосредственно параллаксов заключается в следующем (рис.108).

На направляющей Н прибора расположены кассеты L и R, с центрами которых совмещены снимки стереопары. Направляющая Н может перемещаться при помощи винта Х на станине прибора вдоль оси абсцисс, а кассета L может дополнительно смещаться при помощи винта Р по направляющей Н. Над кассетами помещены две измерительные нити (марки) m и m^/. Если разместить измерительные марки над центрами кассет (снимков) – позиция 1, то по микрометренному винту Р отсчёт будет равен 0.

Переместив при помощи винта Х оба снимка до совмещения правой марки с точкой а^/, получим смещение левого и правого снимков на величину х_п – позиция 2.

Если теперь переместить при помощи винта Р левый снимок, оставляя, правый на месте, до совмещения левой измерительной марки с точкой а – позиция 3, общее расстояние, пройденное левым снимком, будет равно искомому значению горизонтального параллакса данной точки, т.е. Р_а = х_л – х_п. В данном случае величина абсциссы х_п имеет отрицательный знак.

Смещение левого снимка из позиции 2 в положение 3 выполняется при помощи микрометренного винта с очень малым шагом и делениями. На практике такой винт называется параллактическим.

Таким образом, для измерения горизонтального параллакса для какой либо точки стереомодели необходимо совместить измерительные марки винтами Х (абсцисс) и Р (параллаксов) с наблюдаемыми точками левого и правого снимков. Однако такое раздельное совмещение измерительных марок с одноимёнными точками левого и правого снимков не всегда возможно, например, при нивелировании трассы, когда пикетные точки нанесены на одном фотоснимке и отсутствуют на другом. Поэтому на практике измерение параллакса производится способом стереоскопического совмещения марки со стереомоделью. Для этого используется стереоскопическое зрение при рассматривании пары снимков, т.е. наблюдательная система (рис. 106) размещается над системой измерения параллаксов (рис. 108).

Совместное использование стереоскопической наблюдательной и измерительной систем позволило создать в зависимости от их назначения целый ряд стереофотограмметрических приборов: стереокомпараторы, стереопроекторы, стереографы, стереоавтографы, стекометры (рис. 109), стереометрографы (рис. 110) и т.д.

При разработке современных стереофотограмметрических приборов постоянно совершенствуются как наблюдательная система, так и измерительная.

Рис. 109. Общий вид стекометра

Рис. 110. Общий вид измерительной системы стереометрографа.

Наблюдательная система позволяет осуществлять коррекцию зрения наблюдателя, увеличивать наблюдаемые изображения, а измерительная система повышать точность измерений и фиксировать результаты измерений на устройствах, совместимых с вычислительной техникой.

В настоящее время разработаны стереофотограмметрические приборы, совместимые с ЭВМ, позволяющие измеренные величины переводить непосредственно в цифровую топогеодезическую информацию о местности или создавать на графопостроителях топографические планы (рис. 111).

Стереофотограмметрический комплекс АСФК состоит из стереокомпаратора, персонального компьютера, программного обеспечения, графопостроителя, что позволяет создавать и измерять стереомодели местности, получать и хранить цифровую информацию о местности или создавать на графопостроителях непосредственно топографические планы.

Рис. 111. Общий вид автоматизированного

стереофотограмметрического комплекса АСФК

Фотограмметрическое нивелирование имеет ряд достоинств по сравнению с традиционными способами нивелирования. Если анализировать формулу (158), то можно отметить, что в этом выражении только один аргумент является переменным, а именно продольный параллакс. Следовательно, целесообразно определять его изменение на нивелируемых точках относительно исходной точки на данной стереопаре и здесь не происходит традиционного накопления погрешностей нивелирования. В этом случае точность определения отметок нивелируемых точек на данной стереопаре будет зависеть от погрешности взаимного и внешнего ориентирования изображений на приборе.

Кроме этого преимущества достоинство фотограмметрического нивелирования отражается в методике рисовки горизонталей на стереопаре. Если в выражении (158) не изменять величину Δp разности продольных параллаксов, то значение превышения h, а, следовательно, и отметки будет постоянно. Тогда, отметив на одном из изображений стереопары точки стереоскопического касания марки поверхности стереомодели, получим линию равных высот, т.е. горизонталь. Изменив величину продольного параллакса, снова отмечаем точки стереоскопического касания марки поверхности стереомодели и получаем новую горизонталь. В этом и заключается особенности метода стереоскопической рисовки рельефа – отсутствует процесс интерполирования и погрешности обобщения, сглаживания рельефа.