3.6.1.3. Определение расстояния,
недоступного для непосредственного измерения
В тех случаях, когда непосредственное измерение расстояния между двумя точками местности оказывается невозможным, широко применяются косвенные методы, связанные или с геодезическими построениями геометрических фигур функционально связывающих искомые величины с измерениями в этих построениях углов и длин линий (аналитические методы), или с применением оптико-физических способов измерений расстояний (с применением дальномеров).
В первом случае геометрические фигуры образуют, в общем-то, прямую геодезическую засечку (рис. 63).
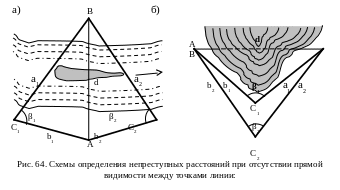
Допустим, необходимо определить длину отрезка АВ. При этом здесь возможны следующие варианты: в одном случае одна из точек искомой линии АВ при наличии прямой видимости недоступна для угловых измерений (рис. 64,а), в другом случае все точки геодезических построений доступны для угловых измерений (рис. 63,б).
В обоих случаях при доступной точке А разбиваются два базиса b1 и b2 и при них измеряются прибазисные углы β1, β2, β3 и β4. Углы при второй точке в первом случае ввиду ее недоступности определяются как дополнения до 1800, т.е.
γ1 = 1800 – (β1 + β2),
γ2 = 1800 – (β3 + β4).
а) б)
b1
b2 
Как видим, в первом случае отсутствует контроль угловых измере- ний в треугольниках АС1В и АВС2. Во втором же случае такой контроль существует, так как сумма углов в треугольнике должна равняться 1800; отклонение от этой величины называют угловой невязкой
fβ1 = β1 + β3 + β5 – 1800,
fβ2 = β2 + β4 + β6 – 1800.
Во втором случае эти углы измеряются – β5 и β6.
Если полученные невязки не превышают допустимого значения, которое для работ технической точности будет равно
доп.
fβ
= 1/
= 1,7/,
то их распределяют на каждый угол поровну с обратным знаком, т.е. в каждый измеренный угол вводят поправку
=
–
и вычисляют исправленные углы
βисп = βизм + ∆β.
Далее, решая треугольники АС1В и АВС2, по теореме синусов вычисляют искомое расстояние:
в первом случае
d1 = (b1 sin β1)/ sin γ1,
d2 = (b2 sin β4)/sin γ2;
во втором случае
d1 = (b3 sin β1)/sin β5,
d2 = (b2 sin β4)/sin β6.
Если
относительная погрешность разности
будет допусти- ма, то за окончательное
значение принимают среднее из двух
полученных величин, т.е.
dср = 0,5 (d1 + d2).
В случае отсутствия прямой видимости между точками А и В и измерения углов при них невозможно, то в геодезических построениях измеряют длину базисных линий а1 и b1, а2 и b2, а так же угол β между ними (рис. 64). Неприступное расстояние вычисляют по теореме косинусов
d
=
.
Если разность ∆d величин d1 и d2, полученных из решения двух треугольников, не превышает допустимого значения, то за окончательное также принимают среднее из d1 и d2.
Из анализа рис. 64, а видно, что базисные стороны а1 и а2 при наличии прямой видимости вдоль них в свою очередь недоступны для непосредственного измерения. В этом случае применяют комбинирован-ные способы измерений расстояний: базисные стороны b1 и b2 измеряют механическими мерными приборами, а стороны а1 и а2 оптико-физическими, при этом предпочтительнее применение лазерных дальномеров.
