2.2. Метод моментов

При заданном виде закона распределения случайной величины Х неизвестные параметры этого распределения можно оценить, то есть выразить как функцию вариант выборки.

Одним из методов нахождения точечных оценок неизвестных параметров заданного распределения является так называемый метод моментов.

Этот метод состоит в том, что приравниваются соответствующие теоретические и эмпирические моменты и из полученных уравнений находятся оценки параметров. В случае одного параметра в теоретическом распределении для его оценки достаточно составить одно уравнение. Если имеются два параметра в теоретическом распределении, то нужно приравнять соответственно два теоретических и эмпирических момента и т.д.

Для оценки двух параметров закона распределения запишем следующие равенства:

, = ,

где - начальный момент первого порядка закона распределения случайной величины;

- эмпирический момент первого порядка;

- центральный момент второго порядка закона распределения случайной величины;

- центральный эмпирический момент второго порядка.

Так как - математическое ожидание случайной величины , - дисперсия случайной величины , , , то получаем два уравнения:

, .

Пример 10. Имеются данные за шесть месяцев об остатках вкладов населения на счетах некоторого коммерческого банка (млн. руб.):

Месяц	1	2	3	4	5	6
Остатки вкладов	20	24	25	28	27	32

Остатки вклада на первое число каждого месяца являются случайной величиной, для характеристики которой принят показательный закон распределения

( ).

Найти оценку параметра .

Решение.

Так как закон распределения содержит лишь один параметр , то для его оценки требуется составить одно уравнение.

Находим выборочную среднюю:

.

Определяем математическое ожидание:

.

Интегрируя по частям, получаем:

.

Тогда

,

Откуда

.

Последнее равенство является приближенным, так правая часть его является случайной величиной. Таким образом, из полученного уравнения получается не точное значение , а его оценка :

.

2.3. Метод максимального правдоподобия

Пусть , ,…, - выборка, полученная в результате проведения независимых наблюдений за случайной величиной . И пусть вид закона распределения величины , например вид плотности , известен, но неизвестен параметр , которым определяется этот закон. Требуется по выборке оценить параметр .

Метод максимального правдоподобия, предложенный Р.Фишером, опирается на использование условий экстремума функции одной или нескольких случайных величин. В качестве такой функции принимают функцию правдоподобия.

Для дискретной случайной величины функция правдоподобия принимает вид

,

где , ,…,  варианты выборки;

 параметр, для которого находится оценка;

 вероятность события , зависящая от параметра .

Для непрерывных случайных величин функция правдоподобия имеет вид:

,

где плотность распределения случай ной величины .

Из определения следует, что чем больше значение функции , тем более вероятно (правдоподобнее) появление при фиксированном в результате наблюдений чисел , ,…, .

За точечную оценку параметра , согласно методу максимального правдоподобия , берут такое его значение , при котором функция правдоподобия достигает максимума.

Так как функции и достигают максимума при одном и том же значении , то вместо отыскания максимума функции ищут (что проще) максимум функции .

Таким образом, для нахождения оценки максимального правдоподобия надо:

1. решить уравнение правдоподобия

;

2. отобрать то решение, которое обращает функцию в максимум. Удобно использовать вторую производную: если

,

то  точка максимума (достаточное условие).

Если оценке подлежат несколько параметров , ,…, распределения, то оценки определяются решением системы уравнений правдоподобия:

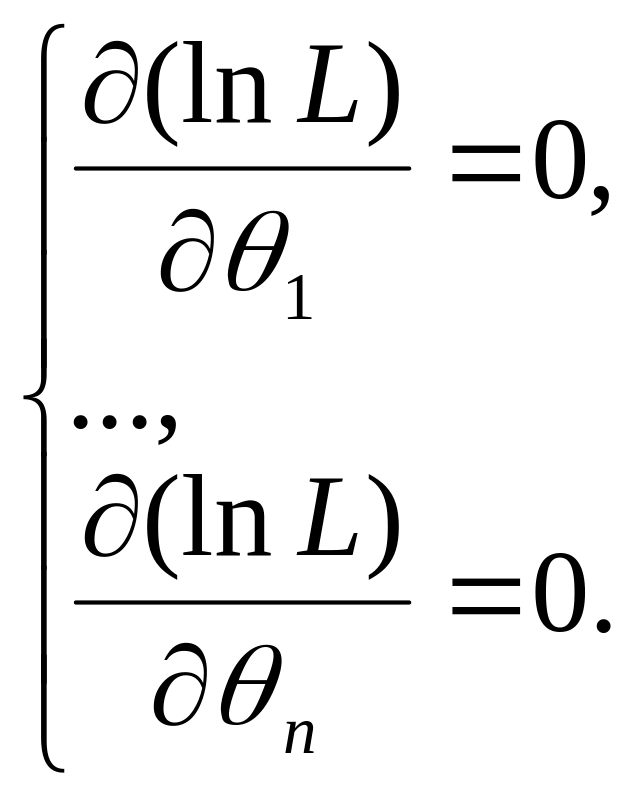
Чаще всего метод максимального правдоподобия используется при биномиальном, пуассоновском и показательном распределениях случайной величины.

В случае биномиального распределения

,

где вероятность появления ровно раз события (случайной величины) в испытаниях;

вероятность появления события в одном испытании.

Величина может рассматриваться как параметр.

Если проводится опытов по испытаний в каждом и фиксируется число появлений события (величины) в каждом испытании , то при подстановке этого значения в формулу биномиального распределения получаем:

.

Тогда функция правдоподобия примет вид:

.

После логарифмирования и приравнивания к нулю производной от получаем выражение для оценки

.

Если значения встречаются раз, то оценка параметра примет вид:

,

где число опытов по испытаний в каждом.