Решение.
1. Для определения тесноты связи вычислим коэффициент корреляции, для чего составим расчетную таблицу:
-
1
2
3
4
5
6
1
84
6,0
7056
36,00
504,0
2
87
5,7
7569
32,49
495,9
3
90
6,1
8100
37,21
549,0
4
99
7,3
9801
53,29
722,7
5
105
8,0
11025
64,00
840,0
6
110
9,5
12100
90,25
1045,0
7
115
9,0
13225
81,00
1035,0
8
125
11,0
15625
121,00
1375,0
9
132
10,2
17424
104,04
1346,4
10
140
12,6
19600
158,76
1764,0
11
143
12,7
20449
161,29
1816,1
12
150
13,0
22500
169,00
1950,0
13
160
14,5
25600
210,25
2320,0
14
165
15,0
27225
225,00
2475,0
15
175
16,1
30625
259,21
2817,5
16
190
17,4
36100
302,76
3306,0
17
200
17,5
40000
306,25
3500,0
18
205
18,0
42025
324,00
3690,0
19
220
19,7
48400
388,09
4334,0
20
240
22,0
57600
484,00
5280,0
2935
251,3
472049
3607,89
41165,6
Коэффициент корреляции рассчитывается по формуле:
.
а) Найдем средние значения:
(сумма значений второго столбца, деленная на число строк:
;
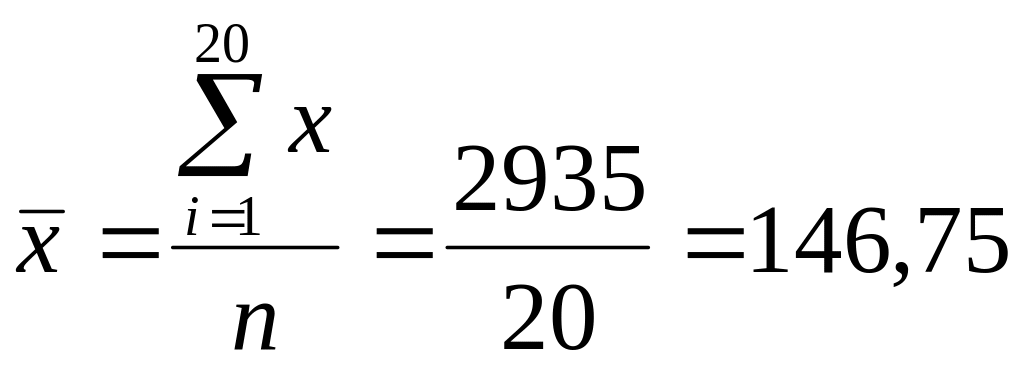(сумма значений третьего столбца, деленная на число строк):
;
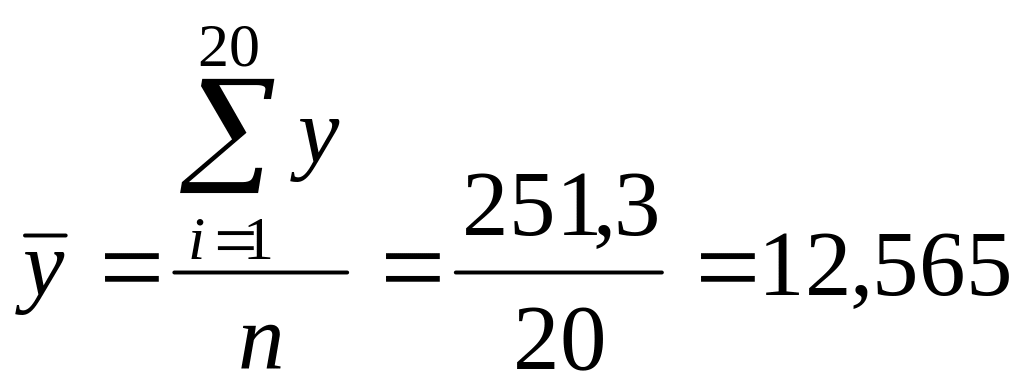(среднее значение шестого столбца):
.
б)
Найдем средние квадратические отклонения
и
:
где рассчитывается как среднее значение четвертого столбца.
Аналогично
,
где - среднее значение пятого столбца.
в) Подставляя найденные значения в формулу коэффициента корреляции, получим:
.
2. Найдем уравнение линейной регрессии.
а) Для определения параметров и линии регрессии составим систему нормальных уравнений:
б)
Подставляя найденные в предыдущем
пункте задачи средние значения
,
,
,
,
получим:
в).
Решая эту систему, найдем
;
-2,11.
Тогда уравнение регрессии имеет вид:
.
3. Таким образом, можно сделать вывод, что связь между мощностью двигателя и расходом бензина прямая и очень тесная, так как полученный коэффициент корреляции положительный и очень близок к единице. Это говорит о том, что чем больше мощность двигателя ( ), тем больше расход бензина ( ).
Выясним, какая часть вариации обусловлена вариацией , для этого вычислим коэффициент детерминации:
.
То есть вариация расхода бензина ( ) на 98% обусловлена вариацией мощности двигателя ( ).
Положительный
коэффициент регрессии
подтверждает то, что связь между мощностью
двигателя и расходом топлива прямая.
Вычислим коэффициент эластичности:
.
Полученный коэффициент свидетельствует о том, что при увеличении мощности двигателя на 1%, расход бензина в среднем увеличится на 1,17 %.