Занятие 12. Корреляционный и регрессионный анализ

Корреляционный и регрессионный анализ. Статистическое исследование наличия или отсутствия зависимости между случайными величинами с помощью выборочного коэффициента корреляции. Выделение линейной части этой зависимости с помощью выборочного коэффициента регрессии и выборочного уравнения (линейной) регрессии.

Если в результате осуществления некоторого эксперимента наблюдаются две величины и 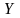, то выборочный корреляционный момент 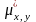величин и определяется формулой:

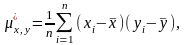
где 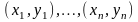— пар наблюденных значений, полученных в независимых повторениях эксперимента,

.

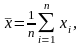
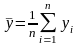Выборочный коэффициент корреляции 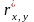равен: 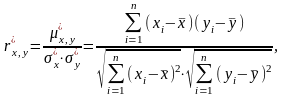где

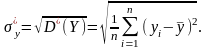
Выборочный коэффициент регрессии на

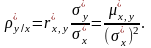
Выборочное уравнение прямой линии регрессии на имеет вид: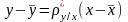 или

выборочно уравнение прямой линии регрессии на 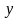: 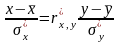или

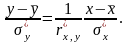
Эти уравнения можно вывести с помощью метода наименьших квадратов.

В качестве оценки отклонения найденного значения от точного значения 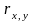коэффициента корреляции берется среднее квадратическое отклонение, приближенно равное:

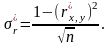
Доверительный интервал для имеет вид:

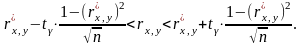
Следовательно, проверка гипотезы о равенстве нулю коэффициента корреляции может быть осуществлена с помощью проверки условия

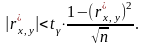
Занятие 13. Дисперсионный анализ

Дисперсионный анализ применяется при изучении влияния совокупности факторов на результаты наблюдения или опыта.

Дисперсионный анализ состоит в оценке отношения дисперсии, характеризующей систематические колебания групповых средних по отдельным факторам, к дисперсии, характеризующей случайное колебание показателей результативного признака.

-распределение Фишера и статистический критерий для проверки гипотезы о сравнении двух дисперсий. Схема однофакторного дисперсионного анализа.

Расчетное задание «Статистическая обработка результатов измерений».

Приложение Варианты индивидуальных заданий

Ниже приведены варианты индивидуальных заданий для выполнения расчетного задания «Статистическая обработка результатов измерений»; -му варианту соответствуют элементы выборки, расположенные в 15-ти последовательных строках таблицы, начиная с -ой (объем выборки при этом . При выполнении работы следует принять уровень значимости 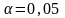, отрезок 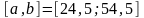, число интервалов .

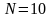1	48	39	43	44	34	34	32	43	40	46
2	25	31	34	49	39	37	45	48	41	49
3	43	46	34	35	42	32	41	34	42	42
4	38	40	46	47	34	42	38	40	38	36
5	30	43	41	40	40	35	35	41	38	45
6	37	42	38	36	44	39	32	48	43	39
7	43	30	32	36	42	34	49	48	49	50
8	37	30	44	48	44	35	45	34	33	41
9	43	45	50	34	33	39	41	39	46	31
10	40	52	44	39	35	45	33	42	42	36
11	44	51	45	39	34	44	40	37	43	32
12	33	42	40	35	37	43	48	48	50	32
13	40	48	45	43	36	39	42	40	37	30
14	44	50	46	39	41	48	44	42	35	51
15	44	50	47	37	33	34	42	43	43	47
16	33	48	38	42	45	32	34	44	39	45
17	48	26	31	34	38	36	46	49	40	48
18	42	47	35	34	41	33	41	35	43	42
19	37	39	47	47	33	42	37	39	40	37
20	43	41	30	39	38	36	34	42	37	46
21	39	44	37	35	43	38	33	47	45	38
22	37	48	38	52	40	45	44	42	38	40
23	44	46	37	34	41	37	41	39	30	38
24	32	41	48	36	51	36	33	39	45	40
25	34	41	38	34	33	27	51	45	27	38
26	42	37	46	41	47	36	30	45	41	40
27	37	37	39	42	48	41	36	39	33	47
28	43	49	27	31	41	46	40	36	36	42
29	41	46	33	37	47	35	31	29	30	36
30	48	38	37	34	40	34	36	50	48	39
31	30	38	43	41	44	45	38	37	46	50
32	41	48	41	43	47	37	42	34	32	44
33	37	48	46	41	41	37	37	48	49	46
34	38	44	50	37	47	27	48	37	46	38
35	48	47	38	52	34	36	34	41	39	28
36	31	43	34	46	37	40	41	41	32	42
37	47	33	51	41	40	45	37	36	27	36
38	37	42	46	35	34	38	45	36	28	40
39	34	48	30	51	33	41	44	42	39	39
40	45	45	41	40	36	27	50	44	41	48
41	36	36	32	32	36	49	27	45	30	38
42	40	38	45	40	40	50	42	37	50	39
43	43	38	30	39	42	41	33	42	38	44
44	44	41	47	52	51	38	50	39	50	48
45	49	43	52	50	39	30	26	50	27	49
46	27	49	46	39	47	26	49	52	29	44
47	51	53	48	49	53	45	27	43	48	44

Основы выборочного метода и элементы статистический теории оценивания. Генеральная и выборочная совокупности. Вариационный ряд, интервальный вариационный ряд. Полигон, гистограмма. Выборочная функция распределения. Числовые характеристики выборки. Точечное оценивание параметров распределения. Несмещенность, состоятельность и эффективность оценки. Выборочная средняя как оценка генеральной средней. Оценка генеральной дисперсии. Интервальное оценивание параметров распределения. Доверительный интервал и доверительная вероятность. Интервальное оценивание генеральной средней и генеральной дисперсии.

Статистическое исследование зависимостей. Корреляционный и регрессионный анализ. Корреляционная таблица. Выборочный коэффициент корреляции. Построение выборочных линейных уравнений регрессии. Множественная линейная регрессия. Частные и множественные коэффициенты корреляции. Экономические примеры.

Методы статистической проверки гипотез. Статистическая гипотеза. Нулевая и конкурирующая гипотезы. Критерий проверки статистической гипотезы, критическая область. Ошибки первого и второго рода, уровень значимости, мощность критерия. Проверка гипотезы о среднем значении при известной и неизвестной дисперсии. Гипотеза о равенстве генеральных средних. Гипотеза о равенстве генеральных дисперсий. Понятие о критерии согласия. Критерий согласия Пирсона. Критерий согласия Колмогорова.

8