Решите самостоятельно следующие задачи.

Данные своей задачи возьмите из таблицы по последнему номеру в зачетке.

1. В урне N билетов. Из них M выигрышных. Какова вероятность того, что первый вынутый билет окажется выигрышным?

2. Биатлонист стреляет в мишень. Мишень - круг радиуса R см. Биатлонист попадает в мишень с вероятностью 1. Попадание в любую точку мишени равновероятно. Какова вероятность попадания в круг радиуса r см.

3. Имеется собрание из N томов некоего автора. Все N томов расставляются на полке случайным образом на книжной полке. Какова вероятность того, что тома расположатся в порядке 1,2,…N или N...2,1?

4. Имеется собрание из N томов некоего автора. На верхней полке умещается только М томов (М<N). Эти тома берут из томов случайным образом и расставляют на верхней полке случайным порядком. Каков вероятность того, что тома расположатся в порядке 1,2, …, М или М, …, 2, 1?

5. Имеется собрание из N томов некоего автора. На верхней полке умещается только М томов (М<N). Эти тома берут из томов случайным образом и расставляют на верхней полке. Какова вероятность, что для размещения на верхней поле будут выбраны тома 1, 2, …, М?

6. Три стрелка стреляют по мишени. Предполагается, что события попадания в мишень для стрелков независимы и вероятности попадания в мишень равны р₁,р₂, р₃. Какова вероятность того, что:

А) все три выстрела окажутся успешными;

Б) хотя бы один из трех выстрелов окажется успешным;

В) точно один выстрел окажется успешным, два неуспешными?

7. Идет охота на волка. В охоте участвуют 4 охотника. Вероятности выхода волка на первого охотника – р₁,, на второго - р₂, на третьего - р₃, на четвертого - р₄. Вероятность убийства волка первым охотником, если волк вышел на него, - р₁,. Вероятность убийства волка вторым охотником, если волк вышел на него, - р₂. Вероятность убийства волка третьим охотником, если волк вышел на него, - р₃. Вероятность убийства волка четвертым охотником, если волк вышел на него, - р₄. Какова вероятность убийства волка?

8. М% всех мужчин и N% всех женщин – дальтоники. Наугад выбранное лицо оказалось дальтоником. Какова вероятность того, что это мужчина. Число мужчин и женщин одинаково.

9. Футболист бьет пенальти N раз. Вероятности забить при одном ударе – р. Какова вероятность того, что будет забито 3 мяча? Более 2 мячей? Найти математическое ожидание и дисперсию.

10. Случайная величина Х задана рядом распределения.

Хi	-3	0	1	4
Pi	P1	P2	P3	P4

Найти математическое ожидание МХ, дисперсию ДХ, вероятности Р (Х<0), P (X>0), P (-1<X<3).

Для случайной величины Y=2X+6 найти математическое ожидание MY, дисперсию ДY.

11. Количество Х принимаемых за час звонков по домашнему телефону имеет распределение Пуассона. Среднее количество принимаемых за час звонков – λ. Какова вероятность того, что будет принято 3 звонка? Более 2 звонков? Найти математическое ожидание и дисперсию.

12. Функция плотности случайной величины Х имеет вид:

f(x)=	{	0 при X>0
		nx при 0≤x≤√2/n
		0 при x≥√2/n

Найти математическое ожидание, дисперсию, P (0<X<0,1).

13. Случайная величина Х – время ожидания дождя в сутках – имеет равномерное распределение на отрезке [0, N]. Найти математическое ожидание, дисперсию, P (X<5),

P (3<X).

14. Вероятность безотказной работы прибора в течение х часов равна 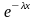. Найти математическое ожидание М – среднюю наработку на отказ и вероятность безотказной работы прибора в течение 100 часов.

15. Случайная величина Х имеет нормальное распределение N(a,σ). a = MX, σ = √DX – среднеквадратичное отклонение. Найти P (X<1), P (-1<X<1), P (-5<X<5), P (- σ<X-а< σ ), P (-2 σ <X-а<2 σ ).

Занятие 9. Оценки неизвестных параметров

Точечные (числовые) оценки параметров распределения. В качестве оценки того или иного параметра берут функции элементов выборки — статистики. Значения статистик изменяются от выборки к выборке, а потому статистики являются случайными величинами. В качестве оценки выбирают такую статистику, значения которой для различных выборок были бы «в среднем» близки к истинному значению параметра.

Основные свойства оценок (несмещенность, состоятельность, эффективность), характеризующие их качество. Какие статистики используются при получении оценок числовых характеристик распределения.

Понятия выборочного среднего, выборочной дисперсии, исправленной выборочной дисперсии. Несмещенность выборочного среднего как оценки математического ожидания и исправленной выборочной дисперсии как оценки дисперсии.

Формулы для вычисления выборочных моментов (начальных и центральных).

Два метода нахождения оценок параметров: метод моментов и метод максимального правдоподобия.

ЗАДАЧА 1. Найти оценку для параметра 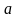экспоненциального распределения, имеющего плотность

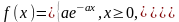используя выборку .

ЗАДАЧА 2. Найти оценку для параметра распределения Пуассона, имеющего закон распределения

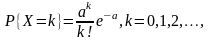используя выборку, определяемую таблицей

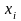
	0	1	2	3	4
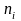
	132	43	20	3	2

ЗАДАЧА 3. Двумя методами (методом моментов и методом максимального правдоподобия) найти оценку для параметра 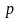распределения Бернулли, имеющего закон распределения

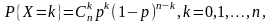
используя выборку, определяемую таблицей

	0	1	2	3	4
	5	2	1	1	1

Занятие 10. Доверительные интервалы

Интервальные оценки параметров распределения. Понятия доверительного интервала и доверительной вероятности (надежности) 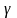. Общие принципы построения доверительных интервалов. Для оценки по результатам 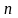наблюдений математического ожидания 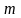нормально распределенной случайной величины 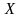при условии, что дисперсия 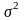известна, служит доверительный интервал:

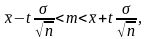
где — объем выборки, 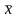— выборочное среднее, а 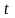— такое значение аргумента функции Лапласа 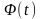, при котором .

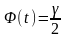Распределение «хи-квадрат» и - распределение Стьюдента. Построение доверительных интервалов для при неизвестном 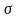и доверительных интервалов для ( — математическое ожидание, а — среднее квадратическое отклонение нормально распределенной случайной величины .
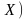