Перечень типовых задач по теме «Аналитическое выражение движений»

Предварительно необходимо:

● изучить по конспектам лекций или по учебнику [4] теоретические сведения по теме «Аналитическое выражение движений и его частные случаи»;

● познакомиться с решениями задач из методического пособия [1]: тема 7, задачи 1.1, 1.2.

Задачи для решения на практическом занятии: [1], тема 7, №№ 2.1 − 2.4, 2.6.

Дополнительно:

1. Найти аналитическое выражение параллельного переноса на вектор 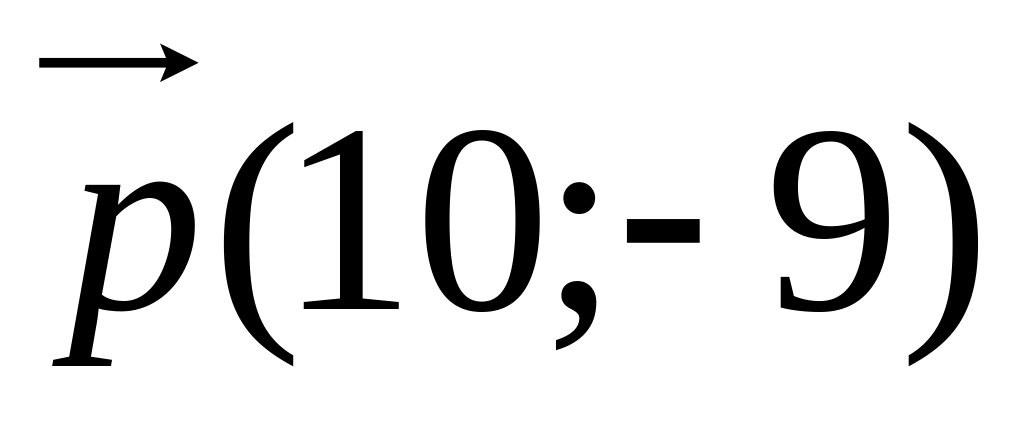и координаты образа 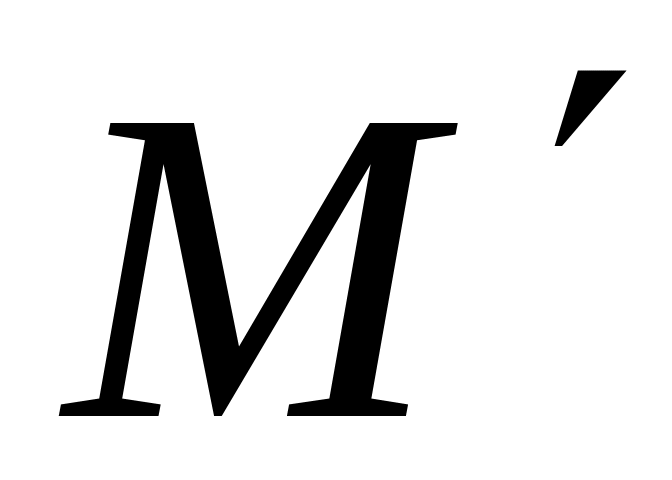и прообраза точки М (1; 2) в данном параллельном переносе.

2. Найти аналитическое выражение поворота вокруг начала координат на угол 120º; −45º.

3. Найти координаты образа и прообраза точки М при симметрии относительно а) оси абсцисс; б) оси ординат.

Задачи для самостоятельного решения: [1], тема 7, №№ 3.1, 3.3, 3.4.

Перечень типовых задач по теме «Подобия плоскости, гомотетия, их свойства»

Предварительно необходимо:

● изучить по конспектам лекций или по учебнику [4] теоретические сведения по теме «Подобия плоскости. Гомотетия»;

● познакомиться с решением задачи 1.1 из методического пособия [1] (тема 9).

Задачи для решения на практическом занятии: [1], тема 9, №№ 2.1, 2.2, 2.5.

Дополнительно:

1. Построить образ прямого угла АВС в гомотетии с центром М₀ и коэффициентом 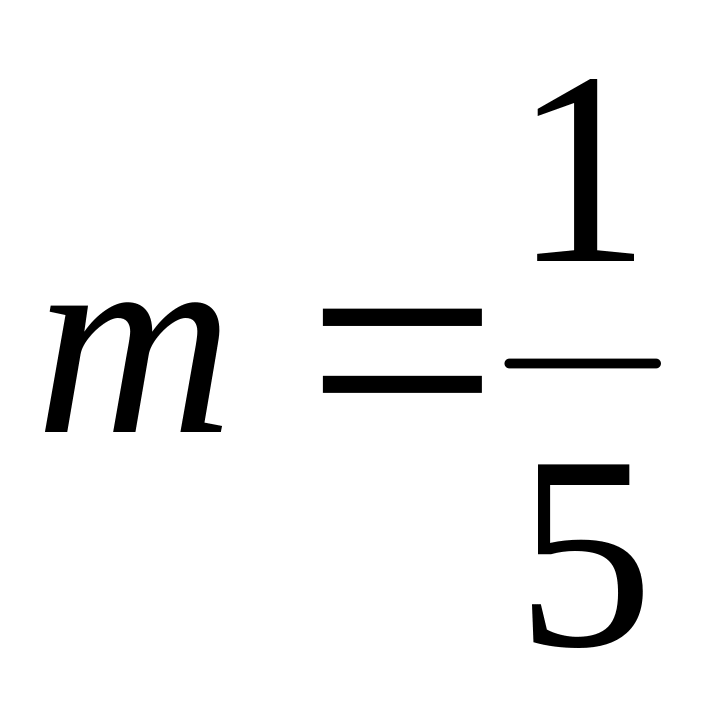; , если: а) точка М₀ лежит внутри угла АВС; б) точка М₀ лежит вне угла АВС.

2. Гомотетия задана центром гомотетии М₀ и парой соответственных точек . Построить образ данной точки Р.

Задачи для самостоятельного решения: [1], тема 9, №№ 3.1, 3.2, 3.4.

Перечень типовых задач по теме «Аналитическое выражение гомотетии и подобия»

Предварительно необходимо:

● изучить по конспектам лекций или по учебнику [4] теоретические сведения по указанной теме;

● познакомиться с решением задачи 1.2 из методического пособия [1] (тема 9).

Задачи для решения на практическом занятии:

1. Найти аналитическое выражение гомотетии с центром в начале координат и коэффициентом m = 6 и координаты образа и прообраза точки М (−5; 3).

2. Найти аналитическое выражение гомотетии с центром в точке М₀(8; −4) и коэффициентом и координаты образа и прообраза начала координат.

3. Дано аналитическое выражение подобия плоскости f:

Определить, будет ли подобие f подобием I рода или II рода. Вычислить определитель матрицы данного преобразования. Найти координаты образа и прообраза начала координат.

Задачи для самостоятельного решения:

1. [1], тема 9, № 3.3

2. Дано аналитическое выражение подобия плоскости g:

Определить род подобия g. Вычислить определитель матрицы данного преобразования. Найти координаты образа и прообраза точки М (1; −7).

Перечень типовых задач по теме

«Аффинные преобразования плоскости, их свойства

и аналитическое выражение.

Перспективно-аффинные преобразования плоскости, их свойства»

Предварительно необходимо:

● изучить по конспектам лекций или по учебнику [4] теоретические сведения по указанным темам;

● познакомиться с решениями задач из методического пособия [1]: тема 10, задачи 1.1 − 1.3.

Задачи для решения на практическом занятии: [1], тема 10, №№ 2.1 − 2.6.

Задачи для самостоятельного решения:

1. Построить образ точки Х в перспективно-аффинном преобразовании f, заданном осью d₀ и парой соответственных точек , если:

а) ; б) ;

в) ; г) .

2. Аффинное преобразование плоскости задано формулами:

а) Определить род этого преобразования;

б) Найти координаты образа и прообраза точки N (−1; 3).

3. Выяснить, будет ли преобразование аффинным.