2 Курс, 4 семестр

Составитель: кандидат физико-математических наук,

доцент Л.Т. Крежевских

Глазов 2012

Геометрия и топология

IV семестр

Модуль 1: Изображение фигур в параллельной проекции.

Модуль 2: Аксонометрия.

Модуль 3: Эпюр двух и трёх проекций.

Практические занятия

№ практического занятия	Тема практического занятия
Практические занятия №1, 2	Изображение плоских и пространственных фигур в параллельной проекции.
Практические занятия №3, 4	Построение сечений призм и пирамид.
Контрольная работа по темам модуля 1 (2 часа)
Практическое занятие №5	Позиционные задачи в аксонометрии.
Практическое занятие №6	Метрические задачи в аксонометрии.
Контрольная работа по темам модуля 2 (2 часа)
Практические занятия №7, 8	Решение позиционных задач на эпюре двух проекций.
Практические занятия №9, 10	Решение метрических задач на эпюре двух проекций.
Практическое занятие №11	Эпюр трёх проекций.
Контрольная работа по темам модуля 3 (2 часа)

Список литературы для подготовки к практическим занятиям

1. Атанасян Л.С., Базылев В.Т. Геометрия. Часть 2. − М.: Просвещение, 1987.

2. Павлова А.А. Начертательная геометрия. − М.: ВЛАДОС, 2005.

3. Нартова Л.Г., Якунин В.И. Начертательная геометрия. − М.: Дрофа, 2003.

Перечень типовых задач по теме

«Изображение плоских и пространственных фигур

в параллельной проекции»

Предварительно необходимо изучить по конспектам лекций или по учебнику [1] теоретические сведения по темам «Понятие, свойства и аналитическое выражение аффинных отображений. Аффинная эквивалентность фигур», «Параллельное проектирование и его свойства», «Правила изображения плоских фигур в параллельной проекции», «Изображение многогранников в параллельной проекции», «Изображение цилиндра, конуса, шара», «Полные и неполные изображения. Понятие о позиционной задаче».

Задачи

1. Построить изображение: а) прямоугольника с отношением сторон 2:3; б) равнобокой трапеции с отношением оснований 2:5.

2. Построить изображение правильного треугольника, вписанного в окружность.

3. Построить изображение: а) правильного шестиугольника, вписанного в окружность; б) правильного восьмиугольника, вписанного в окружность.

4. Построить изображение правильного шестиугольника, используя свойства правильного шестиугольника.

5. Дано изображение А, В, D трёх вершин и 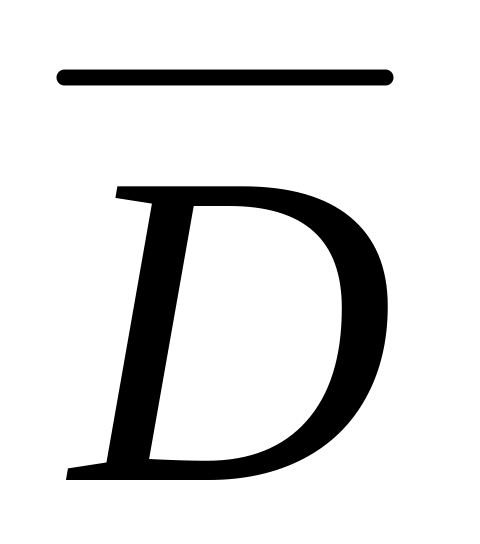правильного шестиугольника . Достроить его изображение.

6. Дано изображение С, D и E трёх соседних вершин правильного шестиугольника. Достроить изображение остальных его вершин.

7. Построить изображение произвольного семиугольника.

8. Построить изображение окружности и её сегмента с углом: а) 30º; б) 60º; в) 45º; г) 75º; д) 105º.

9. Построить изображение окружности и её сектора с углом: а) 30º; б) 60º; в) 45º; г) 75º; д) 105º.

10. Дано изображение произвольного треугольника и двух его высот. Построить изображение центра описанной около этого треугольника окружности.

11. Дано изображение произвольного треугольника, вписанного в окружность. Построить изображение его высот.

12. Построить изображение: а) треугольной призмы, вписанной в цилиндр; б) треугольной призмы, описанной около цилиндра.

13. Построить изображение: а) пятиугольной призмы, вписанной в цилиндр; б) пятиугольной призмы, описанной около цилиндра.

14. Построить изображение: а) треугольной пирамиды, вписанной в конус; б) треугольной пирамиды, описанной около конуса.

15. Построить изображение: а) правильной четырёхугольной пирамиды, вписанной в конус; б) правильной четырёхугольной пирамиды, описанной около конуса.

16. Построить изображение треугольной пирамиды, вписанной в шар.

17. Дано изображение четырёхугольной призмы АВСDA₁B₁C₁D₁, , . Построить точки пересечения прямой (МР) с плоскостями остальных четырёх граней призмы и с диагональной плоскостью (АСС₁).

18. Дано изображение треугольной призмы АВСA₁B₁C₁. Точка М принадлежит верхнему основанию АВС, Р − боковой грани АСC₁A₁. Построить точки пересечения прямой (МР) с плоскостями остальных боковых граней и нижнего основания.

19. Дано изображение четырёхугольной призмы АВСDA₁B₁C₁D₁. Точка М принадлежит грани АВВ₁A₁, Р − грани СDD₁C₁. Построить точки пересечения прямой (МР) с плоскостями остальных четырёх граней призмы и с диагональными плоскостями (АСС₁) и (BDD₁).

20. Дано изображение треугольной пирамиды АВСD. Точка М лежит в плоскости основания АВС (вне основания), Р − в боковой грани. Построить точки пересечения прямой (МР) с плоскостями остальных боковых граней пирамиды.

21. Дано изображение четырёхугольной пирамиды АВСDЕ, , 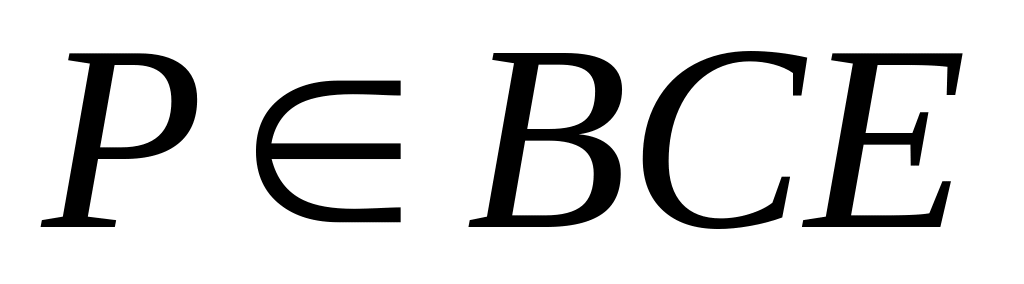. Построить точки пересечения прямой (МР) с плоскостями двух других боковых граней и с плоскостью основания.

22. Дано изображение пятиугольной пирамиды SАВСDЕ (S − вершина), , . Построить точки пересечения прямой (МK) с плоскостями остальных трёх боковых граней и с плоскостью основания.