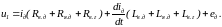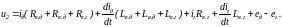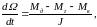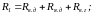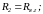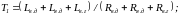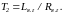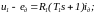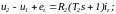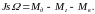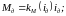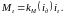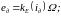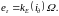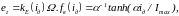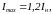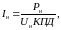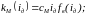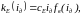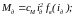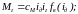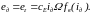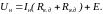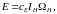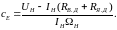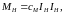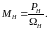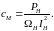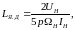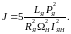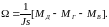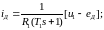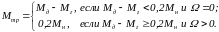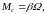1.2 Динамическая модель объекта

Электрическая схема замещения системы «двигатель − генератор» представлена на рисунке 2.

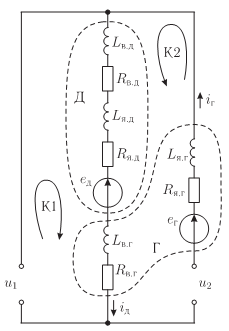
Рисунок 2 – Электрическая схема замещения

В цепи двигателя включены последовательно обе обмотки двигателя (Д): якорная с сопротивлением R_я.д и индуктивностью L_я.д и обмотка возбуждения с сопротивлением R_в.д и индуктивностью L_в.д, а также обмотка возбуждения генератора (Г) с сопротивлением R_в.г и индуктивностью L_в.г. В цепи генератора включена только якорная обмотка генератора с сопротивлением R_я.г и индуктивностью L_я.г. ЭДС e_д и e_г действуют в якорных цепях двигателя и генератора, в которых также протекают токи i_д и i_г, соответственно. На основании второго закона Кирхгофа, записанного для контура К1, выполняется уравнение электрического баланса:

(1)

Уравнение электрического баланса для контура К2 записывается аналогично:

(2)

В уравнения (1) и (2) входят следующие величины: напряжения линейного u₁ и вольтодобавочного u₂ преобразователей, В; ЭДС двигателя e_д и генератора e_г, В; ток цепи двигателя i_д, А; сопротивления R_в.д, R_я.д, R_в.г, Ом; индуктивности L_в.д, L_я.д, L_в.г, Гн.

Уравнение механического баланса получается на основании второго закона Ньютона и имеет вид:

(3)

где Ω − угловая скорость вращения валов электромеханической системы, рад/с; Mд − момент двигателя, Н·м; Mг − момент генератора, Н·м; Mв − суммарный механический момент внешних сил, действующих на вал двигателя и генератора, Н·м; J − момент инерции системы, кг·м².

Введем обозначения:

	(4)
	(5)
	(6)
	(7)

и перепишем уравнения (1) – (3) для изображений сигналов:

	(8)
	(9)
	(10)

Значения вращающих моментов двигателя и генератора зависят от токов в их якорных обмотках и рассчитываются по формулам:

	(11)
	(12)

а связь ЭДС двигателя и генератора с угловой скоростью вращения вала описывается соотношениями:

	(13)
	(14)

Коэффициенты k_M и k_E зависят от конструктивных параметров электрических машин и тока i_д, который протекает в их обмотках возбуждения. Качественный вид зависимостей этих коэффициентов от тока i_д показан на рисунке 3 и может быть описан нелинейной функцией f_в(i_д).

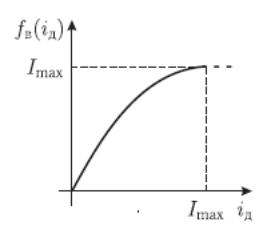
Рисунок 3 – Качественный вид кривой намагничивания

В курсовой работе такие нелинейные функциональные зависимости будем задавать функцией гиперболического тангенса:

(15)

где I_max − ток насыщения; α − параметр нелинейности, α = 2.

Вид гиперболического тангенса при малых значениях i_д имеет зависимость, близкую к линейной, а при приближении значения i_д к I_max плавно переходит в режим насыщения.

Ток насыщения примем равным максимальному току:

(16)

где I_н − номинальный ток двигателя, определяемый по формуле

(17)

где КПД − коэффициент полезного действия двигателя.

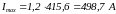
Запишем выражения для функций k_M и k_E:

	(18)
	(19)

где c_M, c_E − постоянные коэффициенты.

Тогда формулы (11) – (14) примут вид:

	(20)
	(21)
	(22)

Значения коэффициентов c_M и c_E определим по паспортным данным двигателя. Рассмотрим схему с последовательным возбуждением ДПТ, которая приведена на рисунке 4.

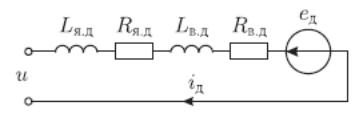
Рисунок 4 – Схема включения двигателя с последовательным возбуждением

Уравнение электрического баланса в установившемся (номинальном статическом) режиме будет иметь вид:

(23)

Значение ЭДС может быть найдено при номинальной скорости вращения по формуле:

(24)

тогда из выражений (23) и (24) следует: с последовательным возбуждением

(25)

В номинальном режиме связь вращающего момента с током описывается соотношением:

(26)

с другой стороны, номинальный момент определяется по выражению:

(27)

Из формул (26) и (27) следует, что

(28)

Приближенное значение индуктивности обмотки якоря 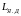вычисляется по формуле:

(29)

где 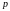− число пар полюсов электродвигателя.

Для простоты будем считать, что все индуктивности равны: .

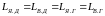Момент инерции примем равным:

(30)

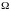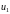Таким образом, после вычисления всех величин, можно окончательно построить динамическую детерминированную модель объекта в виде передаточных функций и связывающих их выражений. Выходной координатой является скорость , а входными воздействиями − напряжения и .

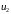Из формулы (10) следует уравнение динамики механической части:

(31)

Выразим токи из формул (8) и (9) и получим уравнения динамики электромагнитной части:

	(32)
	(33)

Формулы (20) – (22) и (31) – (33) описывают работу объекта (системы «двигатель − генератор»), которому соответствует структурная схема, приведенная на рисунке 5.

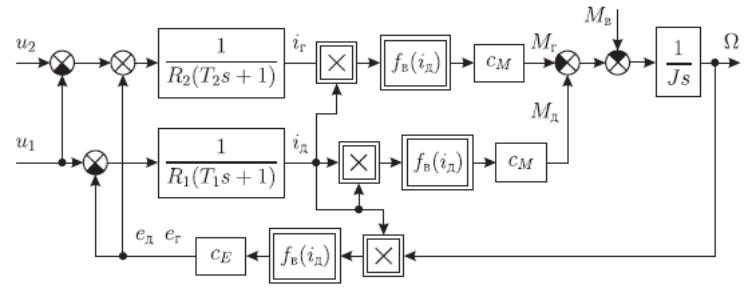
Рисунок 5 – Структурная схема модели объекта при включении тяговых двигателей методом взаимной нагрузки

В курсовой работе будем считать, что момент внешней нагрузки равен нулю (M_вн.н = 0). Значение момента сухого трения M_тр будем считать равным 0,2 M_н. Действие сухого трения приводит к тому, что вращение двигателя начинается лишь после того, как значение момента вращения вала (M_д − M_г) превысит значение M_тр, поэтому при моделировании следует считать, что при малых значениях (M_д − M_г) возмущение M_тр должно компенсировать полезный момент, а после превышения порогового значения возмущение M_тр остается фиксированной величиной, равной 0,2 M_н. Такой алгоритм можно описать выражением:

(34)

Динамическая нагрузка, зависящая от скорости вращения вала, описывается формулой:

(35)

где β – коэффициент,

β = 0,004Mн.

(36)

Таким образом, возмущение M_в состоит из двух составляющих – моментов M_тр и M_с. Для моделирования M_в можно применить подсистему, собранную в пакете Simulink, структура которой представлена на рисунке 6, где переключатель Switch имеет порог переключения, равный малому положительному числу (например, 0,001Ω_н) (этот блок включает верхний входной сигнал, если скорость больше нуля), а блок насыщения Saturation имеет пороговое значение 0,2M_н.

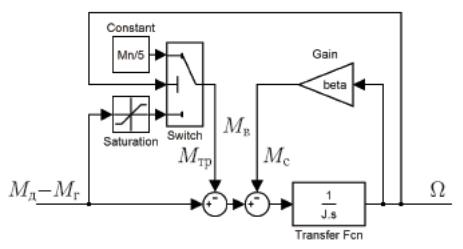
Рисунок 6 – Модель источника возмущений, действующего на момент вращения вала

В соответствии со структурной схемой, представленной на рисунке 5, построим модель объекта в Simulink:

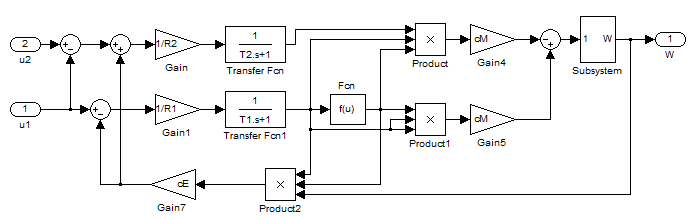
Рисунок 7 – Модель объекта при включении тяговых двигателей методом взаимной нагрузки

Здесь структура блока Subsystem соответствует модели, приведенной на рисунке 6, а блок Fcn реализует нелинейность вида (15).