6. Интерполяционные методы Адамса

Рассмотрим задачу Коши

Пусть з.К. имеет точное решение у(х).На [a,b] постоим с шагом h=(b-a)/N равномерную сетку a=x₀<x₁<_……..<x_n=b.

Для любой гладкой функции у(х) в соответствии с формулой Ньютона-Лейбница выполн-ся рав-во:

.

В интеграле (3) сделаем замену . В рез-те (3) перепишется в виде:

Подинтегральную ф-цию в (4) заменим интерпол-ным многочленом с конечными разностями для интерполирования в конце таблицы, а в качестве узлов интерполирования возьмем точки Получим (5), где остаточный член инетрп мн-члена 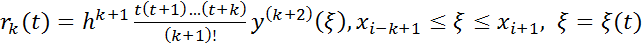, -1≤t≤0

После подстановки (5) в (3) и интегрирования получим: (6), где , С_к= dt Применяя теорему о среднем, получим

M_k+2(7), где M_k+2=max _a≤x≤b| |

Взяв в (6) вместо y инт. кривую ур. (1) , получим:

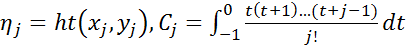, j=i-k+1,..,i

Формула (8) опр-ет инт. метод Адамса решения задачи (1)-(2). Он относится к методам k+1-го порядка точности.

Формула (8) представляет собой нелинейное ур-ие относительно . Поэтому для его решения можно использовать метод простой итерации. На практике часто используют экстрополяционный и интерполяционный метод Адамса вместе, т.е. сначала экс. методом А находят , а затем инт. методом его уточняют (методы прогноза и коррекции).

7. Построение линейны многошаговых методов решения задачи Коши. Примеры

Рассмотрим задачу Коши y’=F(x,y), x [a,b] (1)

y(a)=y­­₀ (2)

На отрезке [a,b] введем сетку x₀=a, x_i=x₀+ih, i=0,1,… . Как правило, линейный к-шаговый метод решения задачи (1)-(2) определяется формулой y_i+1= , i=k,k+1,… (3)

Если =0, то метод (3) называется явным, а при – неявным методом. В основу построения многошаговых метода вида (3) положим алгебраический порядок точности, под которым будем понимать степень многочлена, для которого формула (3) является точной, т.е. погрешность данного метода , т.о. если формула (3) имеет нулевой порядок точности, то она точна для многочлена y(x)=1. Для того, что бы эта функция была решением для уравнения (1), надо что бы y’=0=F(x,y), F=0, тогда для функции

у(х)=1 y_i+1-= . Но поскольку y_i=y(x_i)=1, то получаем условие (4)

Предположим теперь, что формула (3) имеет первый порядок точности, т.е. является такой для функции у(х)=х. Подставляя это равенство в (1) находим F(x,y)=1. Значит (3) можно переписать в виде .

. Из последнего равенства в силу (4) получаем (5)

Условия (4)-(5) называются условиями согласования и являются необходимыми и достаточными для того, что бы многошаговый метод (3) имел по крайней мере 1-ый порядок точности. Если продолжить данные рассуждения, то можно показать, что для того, что бы многошаговый метод (3) имел по крайней мере m-ый порядок точности, необч. и дост. что бы наряду с условиями (4)-(5) еще выполнялось

Пример. Пусть (3) имеет вид: (7). Обозначим . В данном случае условия (4) и (5) таковы . Поэтому (7) можно переписать в виде (8).

Метод (8) точен для любого многочлена первой степени и содержит 1 свободных параметр . Например, если положить , то получим явный метод, который является методом Эйлера. Однако, например можно выбрать и таким образом, чтобы метод (8) был точен для любого многочлена второй степени. Действительно, будем подставлять в (8) функцию: . В данном случае:

(9). Перепишем (9) в виде: (10)

Приведем в (10) подобные слагаемые:

.

А (8) приобретает вид: .