1. Классификация численных методов решения задачи Коши

2. Методы Эйлера, трапеции и Коши-Эйлера решения задачи Коши

3. Методы Рунге-Кутты решения задачи Коши

4. Оценка погрешности и сходимость одношаговых методов

5. Экстраполяционные методы Адамса

6. Интерполяционные методы Адамса

7. Построение многошаговых методов решения задачи Коши. Примеры

8. Условия корней многошаговых методов

9. Сходимость линейных многошаговых методов

1.Классификация численных методов решения з. Коши

Рассмотрим задачу Коши y’(x) = f(x,y(x)), x [a,b] (1)

y(a) = (2) .

При построении численных методов решения задачи (2) (как впрочем и при построении численных методов решения краевых задач)предполагается, что решение исходной задачи существует и удовлетворяет условию единственности.

На отрезке [a,b] зададим сетку (3). Под задачей численного решения задачи (1) – (2) будем понимать нахождение приближенных значений решения y(x) в задаче (2) в узлах сетки (3). То есть итогом численного решения задачи (1) – (2) будет набор чисел , где .

Как правило численные методы решения задачи (1) – (2) представляют собой формулу вида (4)

Рассмотрим классификацию численных методов:

1. Метод (4) вида: называется одношаговый явный.

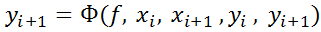2. Метод называется одношаговый неявный.

3. Метод вида: называется к-шаговым явным.

4. - к-шаговым неявным.

5. Методы , у которых в (4) s > 1 называются методами с забеганиями вперёд.

Из приведённой классификации следует, что явные методы представляют собой рекуррентные формулы, позволяющие по известным , (k ) вычислить . Что касается неявных методов, то они представляют собой в общем случае нелинейное уравнение относительно неизвестной . Структура данного нелинейного уравнения позволяет применять для его решения метод простой итерации. Начальное приближение вычисляется каким-либо явным методом. Часто вычислительный процесс строят следующим образом: сначала находят приближенной решение задачи (1) – (2) в точке посредством явного метода. Далее подставляют найденное в правую часть расчётной формулы неявного метода (то есть делают одну итерацию методом простых итераций) находят , то есть указанный процесс осуществляется по 2 указанным формулам:

1. (5)

2. (5)

где - явный и неявный методы.

Методы базирующиеся на использовании 2 формул (5) называются методами прогноза и коррекции. То есть по первой формуле в (5) значения прогнозируется , а по второй уточняется. Применение методов вида (5) как правило обусловлено тем, что погрешность к-шаговых неявных методов меньше погрешностей соответствующих явных методов.

Отметим, что методы с забеганием вперёд на практике используется редко.

2.Методы Эйлера, трапеций, Коши-Эйлера решения з.К

Рассмотрим задачу Коши y’(x)=f(x,y(x)), x [a,b](1). y(a) = (2)

На отрезке [a,b] зададим сетку (3). Для простоты будем считать, что сетка (3) равномерная, то есть . будем обозначать интегральную кривую ур-ния (1),проходящую через точку (x_i,y_i), т.е. = . Указанную интегральную кривую разложим в ряд Тэйлора в окрестности точки : . Учитывая, что интегральная кривая удовлетворяет уравнению (1), начальному условию = , формулу (4) перепишем в виде: . Принимая и отбрасывая в (5) последнее слагаемое получаем рекуррентную формулу: + , (6). Метод решения задачи (1) – (2) основанный на формуле (6) называется методом Эйлера . Значение берётся из формулы (2). Подставим , подставим в (6) находим и так далее. Из формулы (5) следует что , = .

Таким образом погрешность метода Эйлера на одном шаге есть величина порядка O( ). Однако при реализации вычислений по формуле (6) на значение будет влиять не только погрешность метода на одном шаге O( ), но и погрешность с которой найдено значение . То есть при движении по точкам погрешность будет носить накопительный характер. Таким образом общая погрешность метода увеличится в сравнении с погрешностью метода на одном шаге. Далее будет показано , что если погрешность явно метода на одном шаге имеет порядок O( ), то общая погрешность метода имеет порядок O( ). Таким образом метод Эйлера имеет 1ый порядок точности.

Рассмотрим ещё один способ вывода формулы (6). Используем очевидную формулу y( )=y( )+ (7). Если в (7) решения уравнения (1), то (7) можно переписать в виде

y( )=y( )+ (8).

Если к интегралу (8) применить формулу левых прямоугольников (которая отличается от формулы средних прямоугольников только тем , что значение функции берётся не по середине отрезка, а в его левом конце ), то получим y( )= y( )+ .Откуда при использовании соответствующих обозначений следует (6).

Если же интеграл в правой части (8) применить в формуле трапеций, то получим метод трапеций решения задачи (1) – (2). = + (9). Метод (9) является не явным. Сходимость метода простой итерации при достаточно малых h очевидна. Если же величину стоящую в правой части неравенства (9) предварительно вычислить по формуле Эйлера, то получим метод Коши-Эйлера. Он относится к методам прогноза и коррекции и определяется двумя формулами:

=

+ )